NCERT Solutions Ch-7 Congruence of Triangles
Chapter 7 of the NCERT Maths textbook for Class 7 focuses on the concept of congruence of triangles. Congruence refers to the idea that two figures are identical in shape and size, even if they are positioned differently. In this chapter, students learn about the criteria for triangle congruence, which include the Side-Side-Side (SSS) criterion, Side-Angle-Side (SAS) criterion, and Angle-Side-Angle (ASA) criterion. Each criterion provides a method to determine if two triangles are congruent by comparing their sides and angles. The chapter also includes practical applications and geometric constructions to reinforce these concepts, encouraging students to visualize and understand the properties of triangles more deeply. Through various exercises and examples, learners develop critical thinking and problem-solving skills related to geometry.
NCERT Solutions of Chapter 7 Congruence of Triangles exercise 7.1 and 7.2
We try to teach you all Questions in easy way. We solve all chapter wise sums of maths textbook. In every chapter include NCERT solutions. For solutions of Exercise 7.1 and 7.2 click on Tabs :
NCERT Solutions of class 7th maths Chapter 7 Congruence of Triangles exercise 7.1
Q1. Complete the following statements:
(a) Two line segments are congruent if ___________.
Solution:-
Two line segments are congruent if they have the same length.
(b) Among two congruent angles, one has a measure of 70o; the measure of the other angle is ___________.
Solution:-
Among two congruent angles, one has a measure of 70o; the measure of the other angle is 70o.
Because, if two angles have the same measure, they are congruent. Also, if two angles are congruent, their measure are same.
(c) When we write ∠A = ∠B, we actually mean .
Solution:-
When we write ∠A = ∠B, we actually mean m ∠A = m ∠B.
2. Give any two real-life examples for congruent shapes.
Solution:-
The two real-life example for congruent shapes are,
(i) Fan feathers of same brand.
(ii) Size of chocolate in the same brand.
(iii) Size of pens in the same brand
3. If ΔABC ≅ ΔFED under the correspondence ABC ↔ FED, write all the corresponding congruent parts of the triangles.
Solution:-
Two triangles are congruent if pairs of corresponding sides and corresponding angles are equal.
All the corresponding congruent parts of the triangles are,
∠A ↔ ∠F, ∠B ↔ ∠E, ∠C ↔ ∠D
Two triangles are congruent if pairs of corresponding sides and corresponding angles are equal.
All the corresponding congruent parts of the triangles are,
∠A ↔ ∠F, ∠B ↔ ∠E, ∠C ↔ ∠D
Correspondence between sides:
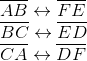
4. If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to
(i) ∠E (ii)  (iii) ∠F (iv)
(iii) ∠F (iv) 
From above the figure we can say that,
The part(s) of ΔBCA that correspond to,
(i) ∠E ↔ ∠C
(ii)
(iii) ∠F ↔ ∠A
(iv)
NCERT Solutions of class 7th maths Chapter 7 Congruence of Triangles exercise 7.2
Q1. Which congruence criterion do you use in the following?
(a) Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
Solution:-
By SSS congruence property:- Two triangles are congruent if the three sides of one triangle are respectively equal to the three sides of the other triangle.
ΔABC ≅ ΔDEF
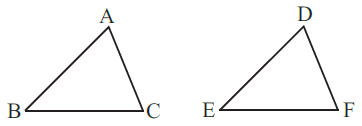
(b) Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ
Solution:-
By SAS congruence property:- Two triangles are congruent if the two sides and the included angle of one are respectively equal to the two sides and the included angle of the other.
ΔACB ≅ ΔDEF
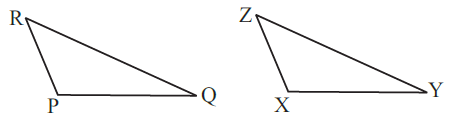
(c) Given: ∠MLN = ∠FGH
∠NML = ∠GFH
∠ML = ∠FG
So, ΔLMN ≅ ΔGFH
Solution:-
By ASA congruence property:- Two triangles are congruent if the two angles and the included side of one are respectively equal to the two angles and the included side of the other.
ΔLMN ≅ ΔGFH
(d) Given: EB = DB
AE = BC
∠A = ∠C = 90o
So, ΔABE ≅ ΔACD
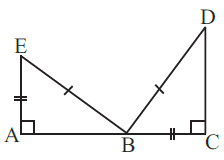
Solution:-
By RHS congruence property:- Two right triangles are congruent if the hypotenuse and one side of the first triangle are respectively equal to the hypotenuse and one side of the second.
ΔABE ≅ ΔACD
2. You want to show that ΔART ≅ ΔPEN,
(a) If you have to use SSS criterion, then you need to show
(i) AR = (ii) RT = (iii) AT =
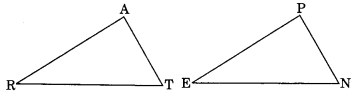
(b) If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
(i) RT = and
(ii) PN =
(c) If it is given that AT = PN and you are to use ASA criterion, you need to have
(i) ZA
(ii) ZT
Solution:
(a) For SSS criterion, we need
(i) AR = PE
(ii) RT = EN
(iii) AT = PN
(b) For SAS criterion, we need
(i) RT = EN and
(ii) PN = AT
(c) For ASA criterion, we need
(i) ∠A = ∠P
(ii) ∠T = ∠N
3. You have to show that ΔAMP ≅ ΔAMQ.
In the following proof, supply the missing reasons.
| Steps | Reasons |
| (i) PM = QM | (i) … |
| (ii) ∠PMA = ∠QMA | (ii) … |
| (iii) AM = AM | (iii) … |
| (iv) ΔAMP ≅ ΔAMQ | (iv) … |
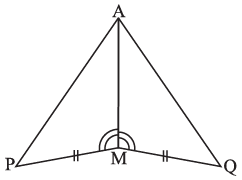
Solution:-
| Steps | Reasons |
| (i) PM = QM | (i) From the given figure |
| (ii) ∠PMA = ∠QMA | (ii) From the given figure |
| (iii) AM = AM | (iii) Common side for the both triangles |
| (iv) ΔAMP ≅ ΔAMQ | (iv) By SAS congruence property:- Two triangles are congruent if the two sides and the included angle of one are respectively equal to the two sides and the included angle of the other. |
4. In ΔABC, ∠A = 30o, ∠B = 40o and ∠C = 110o
In ΔPQR, ∠P = 30o, ∠Q = 40o and ∠R = 110o
A student says that ΔABC ≅ ΔPQR by AAA congruence criterion. Is he justified? Why or Why not?
Solution:-
No, because the two triangles with equal corresponding angles need not be congruent. In such a correspondence, one of them can be enlarged copy of the other.
5. In the figure, the two triangles are congruent. The corresponding parts are marked. We can write ΔRAT ≅ ?
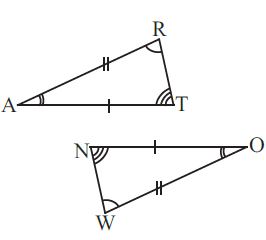
Solution:-
From the given figure,
We may observe that,
∠TRA = ∠OWN
∠TAR = ∠NOW
∠ATR = ∠ONW
Hence, ΔRAT ≅ ΔWON
6. Complete the congruence statement:
ΔBCA ≅ ΔQRS ≅
Solution:-
First consider the ΔBCA and ΔBTA
From the figure, it is given that,
BT = BC
Then,
BA is common side for the ΔBCA and ΔBTA
Hence, ΔBCA ≅ ΔBTA
Similarly,
Consider the ΔQRS and ΔTPQ
From the figure, it is given that
PT = QR
TQ = QS
PQ = RS
Hence, ΔQRS ≅ ΔTPQ
7. In a squared sheet, draw two triangles of equal areas such that
(i) The triangles are congruent.
(ii) The triangles are not congruent.
What can you say about their perimeters?
Solution:-
(i) 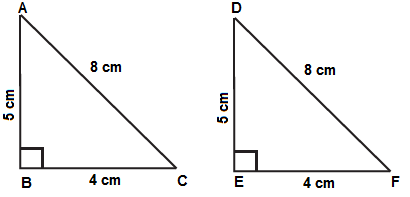
In the above figure, ΔABC and ΔDEF have equal areas.
And also, ΔABC ≅ ΔDEF
So, we can say that perimeters of ΔABC and ΔDEF are equal.
(ii) 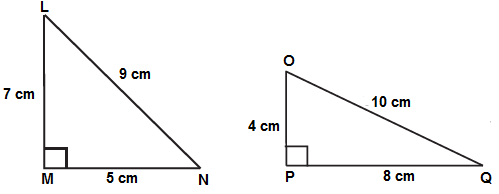
In the above figure, ΔLMN and ΔOPQ
ΔLMN is not congruent to ΔOPQ
So, we can also say that their perimeters are not same.
8. Draw a rough sketch of two triangles such that they have five pairs of congruent parts but still the triangles are not congruent.
Solution:-
Let us draw triangles PQR and STU.
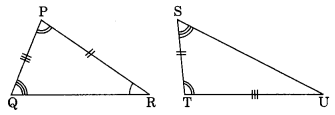
In the above figure, all angles of two triangles are equal. But, out of three sides only two sides are equal.
∠Q = ∠S (Given)
∠P = ∠T (Given)
∠R = ∠U (Given)
Since non of the criteria of congruence is relevant here.
∴ ∆PQR and ∆TSU are not congruent.
9. If ΔABC and ΔPQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
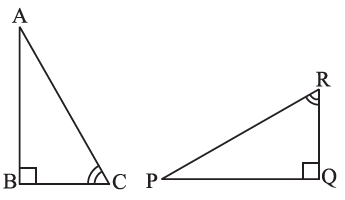
Solution:-
By observing the given figure, we can say that
∠ABC = ∠PQR
∠BCA = ∠PRQ
The other additional pair of corresponding part is BC = QR
∴ ΔABC ≅ ΔPQR
10. Explain, why ΔABC ≅ ΔFED
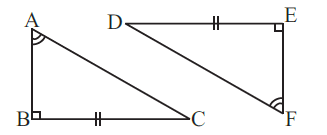
Solution:-
From the figure, it is given that,
∠ABC = ∠DEF = 90o
∠BAC = ∠DFE
BC = DE
By ASA congruence property, two triangles are congruent if the two angles and the included side of one are respectively equal to the two angles and the included side of the other.
ΔABC ≅ ΔFED
