NCERT Solutions Ch-8 Comparing Quantities
Chapter 8 of the NCERT Maths textbook for Class 7, titled “Comparing Quantities,” introduces students to the concept of ratios, percentages, and their applications in everyday life. The chapter begins with a clear explanation of ratios, helping students understand how to express a relationship between two quantities. It then progresses to percentages, showing how to convert fractions and ratios into percentage form and vice versa.
NCERT Solutions of Chapter 8 Comparing Quantities 8.1, 8.2 and 8.3
We try to teach you all Questions in easy way. We solve all chapter wise sums of maths textbook. In every chapter include NCERT solutions. For solutions of Exercise 8.1, 8.2 and 8.3 click on Tabs :
NCERT Solutions of class 7th maths Chapter 8 Comparing Quantities 8.1
1.Find the ratio of:
(a) Rs. 5 to 50 paise
(b) 15 kg to 210 g
(c) 9 m to 27 cm
(d) 30 days to 36 hours
Solution:
(a) Rs. 5 to 50 paise
Converting the given quantities into same units, we have
Rs. 5 = 5 × 100 = 500 paise
∴ Rs. 5 : 50 paise
= 500 paise : 50 paise [∵ Rs. 1 = 100 paise]
= 10 : 1
So, required ratio is 10 : 1.
(b) 15 kg to 210 g
Converting the given quantities into same units, we have
15 kg = 15 × 1000
= 15000 g [∵ 1 kg = 1000 g]
∴ 15 kg : 210 g = 15000 g : 210 g
= 1500 : 21
= 500 : 7
So, the required ratio is 500 : 7.
(c) 9 m to 27 cm
Converting the given quantities into same units, we have
9 m = 9 × 100 = 900 cm
∴ 9m: 27 cm = 900 cm : 27 cm [∵ 1 m = 100 cm]
= 100 : 3
So, the required ratio is 100 : 3.
(d) 30 days to 36 hours
Converting the given quantities into same
units, we have
30 days = 30 × 24 hours [ ∵ 1 day = 24 hours]
= 720 hours
∴ 30 days : 36 hours
= 720 hours : 36 hours = 20:1
So, the required ratio is 20 : 1.
2. In a computer lab, there are 3 computers for every 6 students. How many computers will be needed for 24 students?
Solution:-
From the question it is given that,
Number of computer required for 6 students = 3
So, number of computer required for 1 student = (3/6)
= ½
So, number of computer required for 24 students = 24 × ½
= 24/2
= 12
∴Number of computer required for 24 students is 12 computers.
3. Population of Rajasthan = 570 lakhs and population of UP = 1660 lakhs.
Area of Rajasthan = 3 lakh km2 and area of UP = 2 lakh km2.
(i) How many people are there per km2 in both these States?
(ii) Which State is less populated?
Solution:-
(i) From the question, it is given that,
Population of Rajasthan = 570 lakh
Area of Rajasthan = 3 lakh Km2
Then, population of Rajasthan in 1 km2 area = (570 lakh)/ (3 lakh km2)
= 190 people per km2
Population of UP = 1660 Lakh
Area of UP = 2 Lakh km2
Then, population of UP in 1 lakh km2 area = (1660 lakh)/ (2 lakh km2)
= 830 people per km2
(ii) By comparing the two states Rajasthan is the less populated state.
NCERT Solutions of class 7th maths Chapter 8 Comparing Quantitise 8.2
Q1. Convert the given fractional numbers to percent.
(a) 1/8
Solution:-
In order to convert a fraction into a percentage multiply the fraction by 100 and put the percent sign %.
= (1/8) × 100 %
= 100/8 %
= 12.5%
(b) 5/4
Solution:-
In order to convert a fraction into a percentage multiply the fraction by 100 and put the percent sign %.
= (5/4) × 100 %
= 500/4 %
= 125%
(c) 3/40
Solution:-
In order to convert a fraction into a percentage multiply the fraction by 100 and put the percent sign %.
= (3/40) × 100 %
= 300/40 %
= 30/4 %
= 7.5%
(d) 2/7
Solution:-
In order to convert a fraction into a percentage multiply the fraction by 100 and put the percent sign %.
= (2/7) × 100 %
= 200/7 %
2. Convert the given decimal fraction to percent.
(a) 0.65
Solution:-
First we have to remove the decimal point,
= 65/100
Now,
Multiply by 100 and put the percent sign %.
We have,
= (65/100) × 100
= 65%
(b) 2.1
Solution:-
First we have to remove the decimal point,
= 21/10
Now,
Multiply by 100 and put the percent sign %.
We have,
= (21/10) × 100
=210%
(c) 0.02
Solution:-
First we have to remove the decimal point,
= 2/100
Now,
Multiply 100 and put the percent sign %.
We have,
= (2/100) × 100
= 2%
(d) 12.35
Solution:-
First we have to remove the decimal point,
= 1235/100
Now,
Multiply by 100 and put the percent sign %.
We have,
= (1235/100) × 100)
= 1235%
3. Estimate what part of the figures is coloured and hence find the per cent which is coloured.
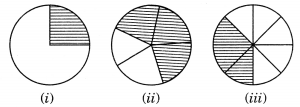
Solution:-
(i)
By observing the given figure,
We can able to identify that 1 part is shaded out of 4 equal parts.
It is represented by a fraction = ¼
Then,
= ¼ × 100
= 100/4
= 25%
Hence, 25% of figure is coloured.
(ii)
By observing the given figure,
We can able to identify that 3 part is shaded out of 5 equal parts.
It is represented by a fraction = 3/5
Then,
= (3/5) × 100
= 300/5
= 60%
Hence, 60% of figure is coloured.
(iii)
By observing the given figure,
We can able to identify that 3 part is shaded out of 8 equal parts.
It is represented by a fraction = 3/8
Then,
= (3/8) × 100
= 300/8
= 37.5%
Hence, 37.5% of figure is coloured.
4. Find:
(a) 15% of 250
Solution:-
We have,
= (15/100) × 250
= (15/10) × 25
= (15/2) × 5
= (75/2)
= 37.5
(b) 1% of 1 hour
Solution:-
We know that, 1 hour = 60 minutes
Then,
1% of 60 minutes
1 minute = 60 seconds
60 minutes = 60 × 60 = 3600 seconds
Now,
1% of 3600 seconds
= (1/100) × 3600
= 1 × 36
= 36 seconds
(c) 20% of Rs. 2500
Solution:-
We have,
= (20/100) × 2500
= 20 × 25
= Rs. 500
(d) 75% of 1 kg
Solution:-
We know that, 1 kg = 1000 g
Then,
75% of 1000 g
= (75/100) × 1000
= 75 × 10
= 750 g
5. Find the whole quantity if
(a) 5% of it is 600
Solution:-
Let us assume the whole quantity be x,
Then,
(5/100) × (x) = 600
X = 600 × (100/5)
X = 60000/5
X = 12000
(b) 12% of it is Rs. 1080.
Solution:-
Let us assume the whole quantity be x,
Then,
(12/100) × (x) = 1080
X = 1080 × (100/12)
X = 540 × (100/6)
X = 90 × 100
X = Rs. 9000
(c) 40% of it is 500k km
Solution:-
Let us assume the whole quantity be x,
Then,
(40/100) × (x) = 500
X = 500 × (100/40)
X = 500 × (10/4)
X = 500 × 2.5
X = 1250 km
(d) 70% of it is 14 minutes
Solution:-
Let us assume the whole quantity be x,
Then,
(70/100) × (x) = 14
X = 14 × (100/70)
X = 14 × (10/7)
X = 20 minutes
(e) 8% of it is 40 liters
Solution:-
Let us assume the whole quantity be x,
Then,
(8/100) × (x) = 40
X = 40 × (100/8)
X = 40 × (100/8)
X = 40 × 12.5
X = 500 liters
6. Convert given percent to decimal fractions and also fractions in simplest forms:
(a) 25%
Solution:-
First convert the given percentage into fraction and then put the fraction into decimal form.
= (25/100)
= ¼
= 0.25
(b) 150%
Solution:-
First convert the given percentage into fraction and then put the fraction into decimal form.
= (150/100)
= 3/2
= 1.5
(c) 20%
Solution:-
First convert the given percentage into fraction and then put the fraction into decimal form.
= (20/100)
= 1/5
= 0.2
(d) 5%
Solution:-
First convert the given percentage into fraction and then put the fraction into decimal form.
= (5/100)
= 1/20
= 0.05
7. In a city, 30% are females, 40% are males and remaining are children. What per cent are children?
Solution:-
From the question, it is given that
Percentage of female in a city =30%
Percentage of male in a city = 40%
Total percentage of male and female both = 40% + 30%
= 70%
Now we have to find the percentage of children = 100 – 70
= 30%
So, 30% are children.
8. Out of 15,000 voters in a constituency, 60% voted. Find the percentage of voters who did not vote. Can you now find how many actually did not vote?
Solution:-
From the question, it is given that
Total number of voters in the constituency = 15000
Percentage of people who voted in the election = 60%
Percentage of people who did not voted in the election = 100 – 60
= 40%
Total number of voters who did not voted in the election = 40% of 15000
= (40/100) × 15000
= 0.4 × 15000
= 6000 voters
∴ 6000 voters did not vote.
9. Meeta saves Rs. 4000 from her salary. If this is 10% of her salary. What is her salary?
Solution:-
Let us assume Meeta’s salary be Rs. x,
Then,
10% of Rs. x = Rs. 4000
(10/100) × (x) = 4000
X = 4000 × (100/10)
X = 4000 × 10
X = Rs. 40000
∴ Meeta’s salary is Rs. 40000.
10. A local cricket team played 20 matches in one season. It won 25% of them. How many matches did they win?
Solution:-
From the question, it is given that
Total matches played by a local team = 20
Percentage of matches won by the local team = 25%
Then,
Number of matches won by the team = 25% of 20
= (25/100) × 20
= 25/5
= 5 matches.
∴The local team won 5 matches out of 20 matches.
NCERT Solutions of class 7th maths Chapter 8 Comparing Quantitise 8.3
Q1. Tell what is the profit or loss in the following transactions. Also find profit per cent or loss per cent in each case.
(a) Gardening shears bought for Rs.250 and sold for Rs. 325.
Solution:-
From the question, it is given that
Cost price of gardening shears = Rs. 250
Selling price of gardening shears = Rs. 325
Since (SP) > (CP), so there is a profit
Profit = (SP) – (CP)
= Rs. (325 – 250)
= Rs. 75
Profit % = {(Profit/CP) × 100}
= {(75/250) × 100}
= {7500/250}
= 750/25
= 30%
(b) A refrigerator bought for Rs. 12,000 and sold at Rs. 13,500.
Solution:-
From the question, it is given that
Cost price of refrigerator = Rs. 12000
Selling price of refrigerator = Rs. 13500
Since (SP) > (CP), so there is a profit
Profit = (SP) – (CP)
= Rs. (13500 – 12000)
= Rs. 1500
Profit % = {(Profit/CP) × 100}
= {(1500/12000) × 100}
= {150000/12000}
= 150/12
= 12.5%
(c) A cupboard bought for Rs. 2,500 and sold at Rs. 3,000.
Solution:-
From the question, it is given that
Cost price of cupboard = Rs. 2500
Selling price of cupboard = Rs. 3000
Since (SP) > (CP), so there is a profit
Profit = (SP) – (CP)
= Rs. (3000 – 2500)
= Rs. 500
Profit % = {(Profit/CP) × 100}
= {(500/2500) × 100}
= {50000/2500}
= 500/25
= 20%
(d) A skirt bought for Rs. 250 and sold at Rs. 150.
Solution:-
Since (SP) < (CP), so there is a loss
Loss = (CP) – (SP)
= Rs. (250 – 150)
= Rs. 100
Loss % = {(Loss/CP) × 100}
= {(100/250) × 100}
= {10000/250}
= 40%
2. Convert each part of the ratio to percentage:
(a) 3 : 1
Solution:-
We have to find total parts by adding the given ratio = 3 + 1 = 4
1st part = ¾ = (¾) × 100 %
= 3 × 25%
= 75%
2nd part = ¼ = (¼) × 100%
= 1 × 25
= 25%
(b) 2: 3: 5
Solution:-
We have to find total parts by adding the given ratio = 2 + 3 + 5 = 10
1st part = 2/10 = (2/10) × 100 %
= 2 × 10%
= 20%
2nd part = 3/10 = (3/10) × 100%
= 3 × 10
= 30%
3rd part = 5/10 = (5/10) × 100%
= 5 × 10
= 50%
(c) 1:4
Solution:-
We have to find total parts by adding the given ratio = 1 + 4 = 5
1st part = (1/5) = (1/5) × 100 %
= 1 × 20%
= 20%
2nd part = (4/5) = (4/5) × 100%
= 4 × 20
= 80%
(d) 1: 2: 5
Solution:-
We have to find total parts by adding the given ratio = 1 + 2 + 5 = 8
1st part = 1/8 = (1/8) × 100 %
= (100/8) %
= 12.5%
2nd part = 2/8 = (2/8) × 100%
= (200/8)
= 25%
3rd part = 5/8 = (5/8) × 100%
= (500/8)
= 62.5%
3. The population of a city decreased from 25,000 to 24,500. Find the percentage decrease.
Solution:-
From the question, it is given that
Initial population of the city = 25000
Final population of the city = 24500
Population decrease = Initial population – Final population
= 25000 – 24500
= 500
Then,
Percentage decrease in population = (population decrease/Initial population) × 100
= (500/25000) × 100
= (50000/25000)
= 50/25
= 2%
4. Arun bought a car for Rs. 3,50,000. The next year, the price went upto Rs. 3,70,000. What was the Percentage of price increase?
Solution:-
From the question, it is given that
Arun bought a car for = Rs. 350000
The price of the car in the next year, went up to = Rs. 370000
Then increase in price of car = Rs. 370000 – Rs. 350000
= Rs. 20000
The percentage of price increase = (Rs. 20000/ Rs. 350000) × 100
= (2/35) × 100
= 200/35
= 40/7
![]()
5. I buy a T.V. for ₹ 10,000 and sell it at a profit of 20%. How much money do I get for it?
Solution:-
From the question, it is given that
Cost price of the T.V. = Rs. 10000
Percentage of profit = 20%
Profit = (20/100) × 10000
= Rs. 2000
Then,
Selling price of the T.V. = cost price + profit
= 10000 + 2000
= Rs. 12000
∴ I will get it for Rs. 12000.
6. Juhi sells a washing machine for Rs. 13,500. She loses 20% in the bargain. What was the price at which she bought it?
Solution:-
From the question, it is given that
Selling price of washing machine = Rs. 13500
Percentage of loss = 20%
Now, we have to find the cost price washing machine
By using the formula, we have:
CP = Rs. {(100/ (100 – loss %)) × SP}
= {(100/ (100 – 20)) × 13500}
= {(100/ 80) × 13500}
= {1350000/80}
= {135000/8}
= Rs. 16875
7. (i) Chalk contains calcium, carbon and oxygen in the ratio 10:3:12. Find the percentage of carbon in chalk.
Solution:-
From the question it is given that,
The ratio of calcium, carbon and oxygen in chalk = 10: 3: 12
So, total part = 10 + 3 + 12 = 25
In that total part amount of carbon = 3/25
Then,
Percentage of carbon = (3/25) × 100
= 3 × 4
= 12 %
(ii) If in a stick of chalk, carbon is 3g, what is the weight of the chalk stick?
Solution:-
From the question it is given that,
Weight of carbon in the chalk = 3g
Let us assume the weight of the stick be x
Then,
12% of x = 3
(12/100) × (x) = 3
X = 3 × (100/12)
X = 1 × (100/4)
X = 25g
∴The weight of the stick is 25g.
8. Amina buys a book for Rs. 275 and sells it at a loss of 15%. How much does she sell it for?
Solution:-
From the question, it is given that
Cost price of book = Rs. 275
Percentage of loss = 15%
Now, we have to find the selling price book,
By using the formula, we have:
SP = {((100 – loss %) /100) × CP)}
= {((100 – 15) /100) × 275)}
= {(85 /100) × 275}
= 23375/100
= Rs. 233.75
9. Find the amount to be paid at the end of 3 years in each case:
(a) Principal = ₹ 1,200 at 12% p.a.
Solution:-
Given: – Principal (P) = Rs. 1200, Rate (R) = 12% p.a. and Time (T) = 3years.
If interest is calculated uniformly on the original principal throughout the loan period, it is called Simple interest (SI).
SI = (P × R × T)/100
= (1200 × 12 × 3)/ 100
= (12 × 12 × 3)/ 1
= Rs.432
Amount = (principal + SI)
= (1200 + 432)
= Rs. 1632
(b) Principal = ₹ 7,500 at 5% p.a.
Solution:-
Given: – Principal (P) = Rs. 7500, Rate (R) = 5% p.a. and Time (T) = 3years.
If interest is calculated uniformly on the original principal throughout the loan period, it is called Simple interest (SI).
SI = (P × R × T)/100
= (7500 × 5 × 3)/ 100
= (75 × 5 × 3)/ 1
= Rs. 1125
Amount = (principal + SI)
= (7500 + 1125)
= Rs. 8625
10. What rate gives ₹ 280 as interest on a sum of ₹ 56,000 in 2 years?
Solution:-
Given: – P = Rs. 56000, SI = Rs. 280, t = 2 years.
We know that,
R = (100 × SI) / (P × T)
= (100 × 280)/ (56000 × 2)
= (1 × 28) / (56 × 2)
= (1 × 14) / (56 × 1)
= (1 × 1) / (4 × 1)
= (1/ 4)
= 0.25%
11. If Meena gives an interest of Rs. 45 for one year at 9% rate p.a. What is the sum she has borrowed?
Solution:-
From the question it is given that, SI = Rs. 45, R = 9%, T = 1 year, P =?
SI = (P × R × T)/100
45 = (P × 9 × 1)/ 100
P = (45 ×100)/ 9
= 5 × 100
= Rs. 500
Hence, she borrowed Rs. 500.
