NCERT Solutions Chapter 13 Exponent and Powers
Chapter 13 of the NCERT Class 7 Maths textbook focuses on Exponents and Powers. This chapter introduces the concept of exponents as a way to express repeated multiplication of a number. For example, an means multiplying a by itself n times. The chapter explains the rules of exponents, such as the product of powers, quotient of powers, and power of a power. It also covers special cases, like zero and negative exponents, and how to simplify expressions involving exponents
NCERT Solutions for Class 7 Maths Chapter 13 Exponents and Powers Ex - 13.1, 13.2 ,13.3
We try to teach you all Questions in easy way. We solve all chapter wise sums of maths textbook. In every chapter include NCERT solutions. For solutions of Exercise 13.1, 13.2. 13.3 click on Tabs :
NCERT Solutions of class 7th maths Chapter 13 Exponents and Powers Exercise 13.1
Question 1. Find the value of
(i) 26
(ii) 93
(iii) 112
(iv) 54
Solution:
(i) 26 = 2 × 2 × 2 × 2 × 2 × 2 = 64
(ii) 93 = 9 × 9 × 9 = 729
(iii) 112 = 11 × 11 = 121
(iv) 54 = 5 × 5 × 5 × 5 = 625
Question 2.
Exress the following in exponential form:
(i) 6 × 6 × 6 × 6
(ii) t × t
(iii) b × b × b × b
(iv) 5 × 5 × 7 × 7 × 7
(v) 2 × 2 × a × a
(vi) a × a × a × c × c × c× c × d
Solution:
(i) 6 × 6 × 6 × 6 = 63
(ii) t × t = t2
(iii) b × b × b × b = b4
(iv) 5 × 5× 7 × 7 × 7 = 52 × 73 = 52 · 73
(v) 2 × 2 × a × a = 22 × a2 = 22 · a2
(vi) a × a ×a × c × c × c × c × d = a3 × c4 × d = a3 · c4 · d
Question 3.
Express each of the following numbers using exponential notation:
(i) 512
Solution:-
The factors of 512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
So it can be expressed in the exponential form as 29.
(ii) 343
Solution:-
The factors of 343 = 7 × 7 × 7
So it can be expressed in the exponential form as 73.
(iii) 729
Solution:-
The factors of 729 = 3 × 3 × 3 × 3 × 3 × 3
So it can be expressed in the exponential form as 36.
(iv) 3125
Solution:-
The factors of 3125 = 5 × 5 × 5 × 5 × 5
So it can be expressed in the exponential form as 55.
Question 4.
Identify the greater number, wherever possible, in each of the following?
(i) 43 or 34
(ii) 53 or 35
(iii) 28 or 82
(iv) 1002 or 2100
(v) 210 or 102
Solution:
(i) 43 or 34
43 = 4 × 4 × 4 = 64,
34 = 3 × 3 × 3 × 3 = 81
Since 81 > 64
∴ 34 is greater than 43.
(ii) 53 or 35
53 = 5 × 5 × 5 = 125
35 = 3 × 3 × 3 × 3 × 3 = 243
Since 243 > 125
∴ 35 is greater than 53.
(iii) 28 or 82
28 =2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256
82 = 8 × 8 = 64
Since 256 > 64
∴ 28 is greater than 28.
(iv) 1002 or 2100
1002 = 100 × 100 = 10000
2100 = 2 × 2 × 2 × … 100 times
Here 2 × 2 × 2 ×2 × 2 × 2 × 2 ×2 × 2 × 2 × 2 × 2 × 2 × 2 = 214 = 16384
Since 16384 > 10,000
∴ 2100 is greater than 1002.
(v) 210 or 102
210 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1024
102 = 10 × 10 = 100
Since 1024 > 100
∴ 210 is greater than 102.
Question 5.
Express each of the following as the product of powers of their prime
(i) 648
Solution:-
Factors of 648 = 2 × 2 × 2 × 3 × 3 × 3 × 3
= 23 × 34
(ii) 405
Solution:-
Factors of 405 = 3 × 3 × 3 × 3 × 5
= 34 × 5
(iii) 540
Solution:-
Factors of 540 = 2 × 2 × 3 × 3 × 3 × 5
= 22 × 33 × 5
(iv) 3,600
Solution:-
Factors of 3600 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5
= 24 × 32 × 52
Question 6.
Simplify:
(i) 2 × 103
(ii) 72 × 22
(iii) 23 × 5
(iv) 3 × 44
(v) 0 × 102
(vi) 52 × 33
(vii) 24 × 32
(viii) 32 × 104
Solution:
(i) 2 × 103 = 2 × 10 × 10 × 10 = = 2000
(ii) 72 × 22 = = 7 × 7 × 2 × 2 = 196
(iii) 23 × 5 = 2 × 2 × 2 × 5 = 40
(iv) 3 × 44 = 3 × 4 × 4 × 4 × 4 = 768
(v) 0 × 102 = 0 × 10 × 10 = = 0
(vi) 52 × 33 = 5 × 5 × 3 × 3 × 3 = 675
(vii) 24 × 32 = 2 × 2 × 2 × 2 × 3 × 3 = 144
(viii) 32 × 104 = 3 × 3 × 10 × 10 × 10 × 10 = 90000
Question 7.
Simplify:
(i) (-4)3
(ii) (-3) × (-2)3
(iii) (-3)2 × (-5)2
(iv) (-2)3 × (-10)3
Solution:
(i) (-4)2 = (-4) × (-4) × (-4) = -64 [∵ (-a)odd number = -aodd number]
(ii) (-3) × (-2)3 = (-3) × (-2) × (-2) × (-2)
= (-3) × (-8) = 24
(iii) (-3)2 × (-5)2 = [(-3) × (-5)]2
= 152 = 225 [∵ am × bm = (ab)m)
(iv) (-2)3 × (-10)3 = [(-2) × (-10)]3
= 202 = 8000 [∵ am × bm = (ab)m]
Question 8.
Compare the following:
(i) 2.7 × 1012; 1.5 × 108
(ii) 4 × 1014; 3 × 1014
Solution:
(i) 2.7 × 1012; 1.5 × 108
Here, 1012 > 108
∴ 2.7 × 1012> 1.5 × 108
(ii) 4 × 1014; 3 × 1017
Here, 1017 > 1014
∴ 4 × 1014 < 3 × 1017
NCERT Solutions of class 7th maths Chapter 13 Exponents and Powers Exercise 13.2
Question 1.
Using laws of e×ponents, simplify and write the answer in e×ponential form:
(i) 32 × 34 × 38
(ii) 615 ÷ 610
(iii) a3 × a2
(iv) 7x × 72
(v) (52)3 ÷ 53
(vi) 25 × 55
(vii) a4 × b4
(viii) (34)3
(ix) (220 ÷ 215) × 23
(x) 8t ÷ 82
Solution:
(i) 32 × 34 × 38 = 32+4+8 = 314 [am ÷ an = am+n]
(ii) 615 ÷ 610 = 615-10 = 65 [am ÷ an = am-n]
(iii) a3 × a2 = a3+2 = a5 [am × an = am+n]
(iv) 7x × 72 = 7x+2 [am × an = am+n]
(v) (52)3 ÷ 53 = 52×3 ÷ 53 = 56 ÷ 53 = 56-3 = 53 [(a3)n = amn, am ÷ an = am-n]
(vi) 25 × 55 = (2 × 5)5 = 105 [am × bm = (ab)m]
(vii) a4 × b4 = (ab)4 [am × bm = (ab)4]
(ix) (220 ÷ 215) × 23 = 220-15 × 23
=25 × 23 = 25+3 = 28
(x) 8t ÷ 82 = 8t-2 [am ÷ an = am-n]
Question 2.
Simplify and express each of the following in exponential form:
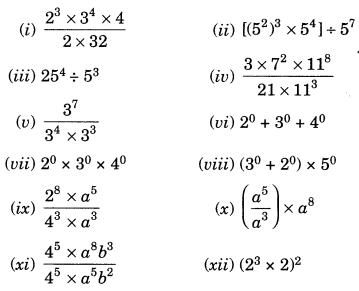
Solutions


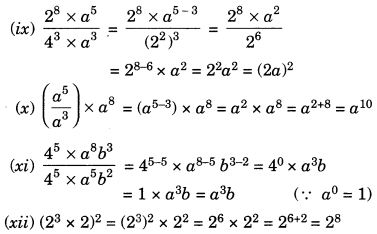
Question 3.
Say true or false and justify your answer:
(i) 10 × 1011 = 10011
(ii) 23 > 52
(iii) 23 × 32 = 65
(iv) 320 = (1000)0
Solution:
(i) 10 × 1011 = 101+11 = 1012
RHS = 10011 = (102)11 = 1022
1012 ≠ 1022
∴ Statement is false.
(ii) 23 > 52
LHS = 23 = 8
RHS = 522 = 25
8 < 25
∴ 23 < 52
Thus, the statement is false.
(iii) 23 × 32 = 65
LHS = 233 × 32 = 8 × 9 = 72
RHS = 65 = 6 × 6 × 6 × 6 × 6 = 7776
∴ 72 ≠ 7776
∴ The statement is false.
(iv) 30 = (1000)0
⇒ 1 = 1 True [∵ a0 = 1]
Question 4.
Express each of the following as a product of prime factors only in exponential form:
(i) 108 × 192
(ii) 270
(iii) 729 × 64
(iv) 768
Solution:
(i) 108 × 192
Solution:-
The factors of 108 = 2 × 2 × 3 × 3 × 3
= 22 × 33
The factors of 192 = 2 × 2 × 2 × 2 × 2 × 2 × 3
= 26 × 3
Then,
= (22 × 33) × (26 × 3)
= 22 + 6 × 33 + 1 … [∵am × an = am + n]
= 28 × 34
(ii) 270
Solution:-
The factors of 270 = 2 × 3 × 3 × 3 × 5
= 2 × 33 × 5
(iii) 729 × 64
The factors of 729 = 3 × 3 × 3 × 3 × 3 × 3
= 36
The factors of 64 = 2 × 2 × 2 × 2 × 2 × 2
= 26
Then,
= (36 × 26)
= 36 × 26
(iv) 768
The factors of 768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3
= 28 × 3
Question 5.
Simplify:
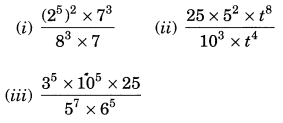
Solution:-


NCERT Solutions of class 7th maths Chapter 13 Exponents and Powers Exercise 13.3
Question 1. Write the following numbers in the e×panded forms:
279404, 3006194, 2806196, 120719, 20068
Solution:
(i) 279404 = 2 × 100000 + 7 × 10000 + 9 × 1000 + 4 × 100 + 0 × 10 + 4
= 2 × 105 + 7 × 104 + 9 × 1032 + 4 × 102 + 0 × 101 + 4 × 100
(ii) 3006194 = 3 × 1000000 + 0 × 100000 + 0 × 10000 + 6 × 1000 + 1 × 100 + 9 × 10 + 4
= 3 × 106 + 0 × 105 + 0 × 104 + 6 × 103 + 1 × 102 + 9 × 101 + 4 × 100
(iii) 2806196 = 2 × 1000000 + 8 × 100000 + 0 × 10000 + 6 × 1000 + 1 × 100 + 9 × 10 + 6
= 2 × 106 + 8 × 105 + 0 × 104 + 6 × 103 + 1 × 102 + 9 × 101 + 6 × 100
(iv) 120719 = 1 × 100000 + 2 × 10000 + 0 × 1000 + 7 × 100 + 1 × 10 + 9
= 1 × 105 + 2 × 104 + 0 × 103 + 7 × 102 + 1 × 101 + 9 × 100
(v) 20068 = 2 × 10000 + 0 × 1000 + 0 × 100 + 6 × 10 + 8
= 2 × 104 + 0 × 103 + 0 × 102 + 6 × 101 + 8 × 100
Question 2.
Find the number from each of the following expanded forms:
(a) 8 × 104 + 6 × 103 + 0 × 102 + 4 × 101 + 5 × 100
(b) 4 × 105 + 5 × 103 + 3 × 102 + 2 × 100
(c) 3 × 104 + 7 × 102 + 5 × 100
(d) 9 × 105 + 2 × 102 + 3 × 101
Solution:
(a) 8 × 104 + 6 × 103 + 0 × 102 + 4 × 101 + 5 × 100
= 8 × 10000 + 6 × 1000 + 0 × 100 + 4 × 10 + 5 × 1
= 80000 + 6000 + 0 + 40 + 5 = 86045
(b) 4 × 105 + 5 × 103 + 3 × 102 + 2 × 100
= 4 × 100000 + 5 × 1000 + 3 × 100 + 2 × 1
= 400000 + 5000 + 300 + 2 = 405302
(c) 3 × 104 + 7 × 102 + 5 × 100
= 3 × 10000 + 7 × 100 + 5 × 1
= 30000 + 700 + 5 = 30705
(d) 9 × 105 + 2 × 102 + 3 × 101
= 9 × 100000 + 2 × 100 + 3 × 10
= 900000 + 200 + 30 = 900230
Question 3.
Express the following numbers in standard form:
(i) 5,00,00,000
(ii) 70,00,000
(iii) 3,18,65,00,000
(iv) 3,90,878
(v) 39087.8
(vi) 3908.78
Solution:
(i) 5,00,00,000 = 5 × 1077
(ii) 70,00,000 = 7 × 106
(iii) 3,18,65,00,000 = 3.1865 × 109
(iv) 3,90,878 = 3.90878 × 105
(v) 39087.8 = 3.90878 × 104
(vi) 3908.7 8 = 3.90878 × 103
Question 4.
Express the number appearing in the following statements in standard form:
(a) The distance between Earth and Moon is 384.0. 000 m.
(b) Speed of light in vacuum is 300,000,000 m/s.
(c) Diameter of the Earth is 1,27,56,000 m.
(d) Diameter of the Sun is 1,400,000,000 m.
(e) In a galaxy there are an average 100,000,000,000 stars.
(f) The universe is estimated to be about 12,000,000,000 years old.
(g) The distance of the Sun from the centre of the Milky Way Galaxy is estimated to be 300,000,000,000,000,000,000 m.
(h) 60,230,000,000,000,000,000,000 molecules are contained in a drop of water weighing 1.8 gm.
(i) The Earth has 1,353,000,000 cubic km of sea water.
(j) The population of India was about 1,027,000,000 in March 2001.
Solution:
(a) 384,000,000 m = 3.84 × 108 m
(b) 300,000,000 m/s = 3 × 108 m/s
(c) 1,27,56,000 m = 1.2756 × 1072 m
(d) 1,400,000,000 m = 1.4 × 109 m
(e) 100,000,000,000 stars = 1 × 1011 stars
(f) 12,000,000,000 years old = 1.2 × 1010 years old
(g) 300,000,000,000,000,000,000 m = 3 × 1020 m
(h) 60, 230, 000, 000, 000, 000, 000, 000 molecules = 6.023 × 1022 molecules
(i) 1,353,000,000 cubic km = 1.353 × 109 cubic km
(j) 1,0,27,000,000 = 1.027 × 109
