NCERT Solutions Ch-4 Practical Geometry
Chapter 4 of NCERT’s Maths textbook for Class 8 focuses on Practical Geometry, which involves constructing various geometrical figures using a compass and straightedge. The chapter emphasizes the steps required to accurately draw angles, triangles, and other shapes, providing clear instructions and illustrations.
Key concepts include:
- Construction of Angles: Students learn to construct angles like 60°, 90°, and 120° using a compass and straightedge.
- Triangles: The chapter covers the construction of triangles based on given measurements of sides and angles, including the SSS (Side-Side-Side) and SAS (Side-Angle-Side) criteria.
- Properties of Geometric Figures: It reinforces understanding of properties like congruence and similarity in geometric constructions.
NCERT Solutions of Class 8th Chapter 4 Practical Geometry Exercise 4.1, 4.2, 4.3, 4.4 and 4.5
We try to teach you all Questions in easy way. We solve all chapter wise sums of maths textbook. In every chapter include NCERT solutions. For solutions of Exercise 4.1, 4.2, 4.3 , 4.4 and 4.5 click on Tabs :
Q.1 Construct the following quadrilaterals.
(i) Quadrilateral ABCD
AB = 4.5 cm, BC = 5.5 cm, CD = 4 cm, AD = 6 cm, AC = 7 cm
(ii) Quadrilateral JUMP
JU = 3.5 cm, UM = 4 cm, MP = 5 cm, PJ = 4.5 cm, PU = 6.5 cm
(iii) Parallelogram MORE
OR = 6 cm, RE = 4.5 cm, EO = 7.5 cm
(iv) Rhombus BEST
BE = 4.5 cm, ET = 6 cm
Solution:
(i) We have to draw first rough sketch.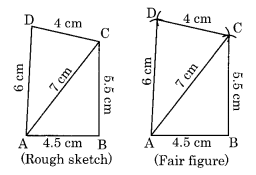
Construction:
Step I: Draw AB = 4.5 cm
Step II: Draw an arc with centre B and radius 5.5 cm.
Step III: Draw another arc with centre A and radius 7 cm to meet the previous arc at C.
Step IV: Draw an arc with centre C and radius 4 cm.
Step V: Draw another arc with centre A and radius 6 cm to cut the former arc at D.
Step VI: Join BC, AC, CD and AD.
(ii) We have to draw the first rough sketch.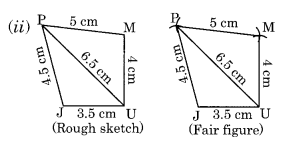
Thus ABCD is the required quadrilateral.
Construction:
Step I: Draw JU = 3.5 cm.
Step II: Draw an arc with centre J and radius 4.5 cm.
Step III: Draw another arc with centre U and radius 6.5 cm to meet the previous arc at P.
Step IV: Join JP and UP.
Step V: Draw an arc with centre U and radius 4 cm.
Step VI: Draw another arc with centre P and radius 5 cm to meet the previous arc at M.
Step VII: Join UM and PM.
Thus, JUMP is the required quadrilateral.
(iii) We have to draw the first rough sketch.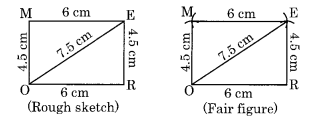
Construction: (Opposite sides of a parallelogram are equal)
Step I: Draw OR = 6 cm.
Step II: Draw an arc with centre R and radius 4.5 cm.
Step III: Draw another arc with centre O and radius 7.5 cm to meet the previous arc at E.
Step IV: Join RE and OE.
Step V: Draw an arc with centre E and radius 6 cm.
Step VI: Draw another arc with centre O and radius 4.5 cm to meet the former arc at M.
Step VII: Join EM and OM.
Thus, MORE is the required parallelogram.
(iv) We have to draw first rough sketch.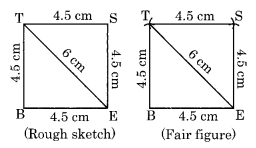
Construction: (All sides of a rhombus are equal)
Step I: Draw BE = 4.5 cm
Step II: Draw an arc with centre B and radius 4.5 cm.
Step III: Draw another arc with centre E and radius 6 cm to meet the previous arc at T.
Step IV: Join BT and ET.
Step V: Draw two arcs with centres E and T with equal radii 4-5 cm to meet each other at S. .
Step VI: Join ES and TS.
Thus, BEST is the required rhombus.
Q.1 Construct the following quadrilaterals.
(i) Quadrilateral LIFT
LI = 4 cm
IF = 3 cm
TL = 2.5 cm
LF = 4.5 cm
IT = 4 cm
(ii) Quadrilateral GOLD
OL = 7.5 cm
GL = 6 cm
GD = 6 cm
LD = 5 cm
OD = 10 cm
(iii) Rhombus BEND
BN = 5.6 cm
DE = 6.5 cm
Solution:
(i) Construction: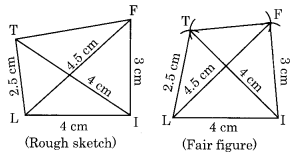
Step I: Draw LI = 4 cm.
Step II: Draw an arc with centre I and radius 3 cm.
Step III: Draw another arc with centre L and radius 4.5 cm to meet the former arc at F.
Step IV: Join LF and IF.
Step V: Draw an arc with centre L and radius 2.5 cm.
Step VI: Draw another arc with centre I and radius 4 cm to meet the previous arc at T.
Step VII: Join LT and IT.
Thus LIFT is the required quadrilateral.
(ii) Construction: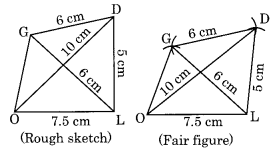
Step I: Draw OL = 7.5 cm
Step II: Draw an arc with centre O and radius 10 cm.
Step III: Draw another arc with centre L and radius 5 cm to meet the previous arc at D.
Step IV: Join OD and LD.
Step V: Draw an arc with centre L and D with equal radii of 6 cm to meet each other at G.
Step VI: Join LG and DG.
Thus GOLD is the required quadrilateral.
(iii) Construction: (The diagonals of a rhombus bisect each other at the right angle)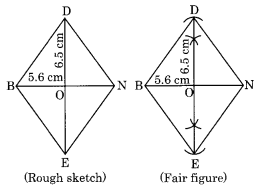
Step I: Draw BN = 5.6 cm.
Step II: Draw the right bisector of BN at O.
Step III: Draw two arcs with centre O and radius 12 × DE, i.e., 12 × 6.5 = 3.25 cm to meet the right bisector at D and E.
Step IV: Join BE, EN, ND and BD.
Thus, BEND is the required rhombus.
Q.1 Construct the following quadrilaterals:
(i) Quadrilateral MORE
MO = 6 cm, ∠R = 105°, OR = 4.5 cm, ∠M = 60°, ∠O = 105°
(ii) Quadrilateral PLAN
PL = 4 cm, LA = 6.5 cm, ∠P = 90°, ∠A = 110°, ∠N = 85°
(iii) Parallelogram HEAR
HE = 5 cm, EA = 6 cm, ∠R = 85°
(iv) Rectangle OKAY
OK = 7 cm, KA = 5 cm
Solution:
(i) Construction:
Step I: Draw OR = 4.5 cm
Step II: Draw two angles of 105° each at O and R with the help of protactor.
Step III: Cut OM = 6 cm.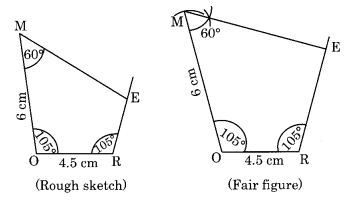
Step IV: Draw an angle of 60° at M to meet the angle line through R at E.
Thus, MORE is the required quadrilateral.
(ii) Construction: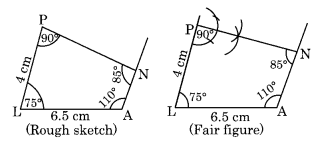
Step I: Draw LA = 6.5 cm
Step II: Draw an angle of 75° at L and 110° at A with the help of a protractor.
[∵ 360° – (110° + 90° + 85°) = 75°]
Step III: Cut LP = 4 cm.
Step IV: Draw an angle of 90° at P which meets the angle line through A at N.
Thus PLAN is the required quadrilateral.
(iii) Construction: (Opposite sides of a parallelogram are equal)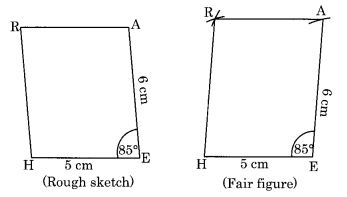
Step I: Draw HE = 5 cm.
Step II: Draw an angle of 85° at E and cut EA = 6 cm.
Step III: Draw an arc with centre A and radius 5 cm.
Step IV: Draw another arc with centre H and radius 6 cm to meet the previous arc at R.
Step V: Join HR and AR
Thus, HEAR is the required parallelogram.
(iv) Construction:
(Each angle of a rectangle is 90° and opposite sides are equal.)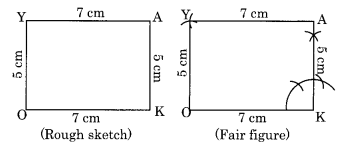
Step I: Draw OK = 7 cm.
Step II: Draw the angle of 90° at K and cut KA = 5 cm.
Step III: Draw an arc with centre O and radius 5 cm.
Step IV: Draw another arc with centre A and radius 7 cm to meet the previous arc at Y.
Step V: Join OY and AY.
Thus OKAY is the required rectangle.
Construct the following quadrilaterals:
(i) Quadrilateral DEAR
DE = 4 cm, EA = 5 cm, AR = 4.5 cm, ∠E = 60°, ∠A = 90°
(ii) Quadrilateral TRUE
TR = 3.5 cm, RU = 3 cm, UE = 4.5 cm, ∠R = 75°, ∠U = 120°
Solution:
(i) Construction: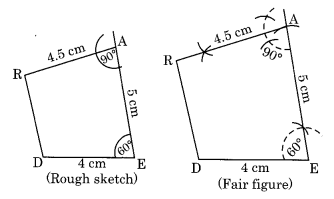
Step I: Draw DE = 4 cm.
Step II: Draw an angle of 60° at E.
Step III: Draw an arc with centre E and radius 5 cm to meet the angle line at A.
Step IV: Draw an angle of 90° at A and cut AR = 4.5 cm.
Step V: Join DR.
Thus, DEAR is the required quadrilateral.
(ii) Construction: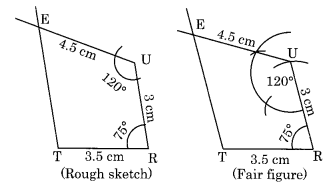
Step I: Draw TR = 3.5 cm
Step II: Draw an angle of 75° at R and cut RU = 3 cm.
Step III: Draw an angle of 120° at U and cut UE = 4.5 cm.
Step IV: Join TE.
Thus, TRUE is the required quadrilateral.
Draw the following:
Q.1 The square READ with RE = 5.1 cm.
Solution:
Construction: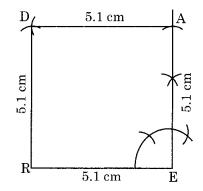
Step I: Draw RE = 5.1 cm.
Step II: Draw an angle of 90° at E and cut EA = 5.1 cm.
Step III: Draw two arcs from A and R with radius 5.1 cm to cut each other at D.
Step IV: Join RD and AD.
Thus, READ is the required square.
Q.2 A rhombus whose diagonals are 5.2 cm and 6.4 cm long.
Solution:
Construction: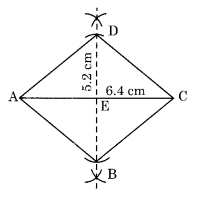
Step I: Draw AC = 6.4 cm.
Step II: Draw the right bisector of AC at E.
Step III: Draw two arcs with centre E and radius = 5.22 = 2.6 cm to cut the previous diagonal at B and D.
Step IV: Join AD, AB, BC and DC.
Thus ABCD is the required rhombus.
Q.3 A rectangle with adjacent sides of lengths 5 cm and 4 cm.
Solution:
Construction: Let the two adjacent sides of a rectangle PQRS be PQ = 5 cm and QR = 4 cm.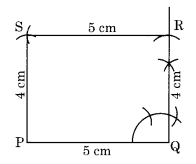
Step I: Draw PQ = 5 cm.
Step II: Draw an angle of 90° at Q and cut QR = 4 cm.
Step III: Draw an arc with centre R and radius 5 cm.
Step IV: Draw another arc with centre P and radius 4 cm to meet the previous arc at S.
Step V: Join RS and PS.
Thus, PQRS is the required rectangle.
Q.4 A parallelogram OKAY where OK = 5.5 cm and KA = 4.2 cm. Is it unique?
Solution:
Construction:
Step I: Draw OK = 5.5 cm.
Step II: Draw an angle of any measure (say 60°) at K and cut KA = 4.2 cm.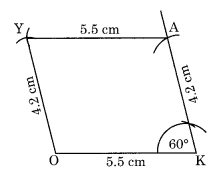
Step III: Draw an arc with centre A and radius of 5.5 cm.
Step IV: Draw another arc with centre O and radius 4.2 cm to cut the previous arc at Y.
Step V: Join AY and OY.
Thus, OKAY is the required parallelogram.
No, it is not a unique parallelogram. The angle at K can be of measure other than 60°.
