NCERT Solutions Ch-13 Surface Areas and Volumes
Chapter 13 of the NCERT Maths textbook for Class 9, titled “Surface Areas and Volumes,” focuses on the measurement of three-dimensional shapes. It covers various geometric figures, including cubes, cuboids, cylinders, cones, and spheres, teaching students how to calculate their surface areas and volumes. The chapter begins with the definitions of surface area and volume, explaining how surface area is the total area of the surfaces of a solid, while volume measures the space occupied by the solid.
The chapter provides formulas for calculating the surface area and volume of each shape. For example, the surface area of a cube is 6a square (where a is the length of a side), while its volume is a cube Similarly, for a cuboid, the surface area is 2(lb+bh+hl) and the volume is (length, breadth, and height).
NCERT Solutions of Class 9th Chapter 13 Surface Areas and Volumes Exercise 13.1, 13.2, 13.3, 13.4, 13.5, 13.6, 13.7, 13.8, 13.9
We try to teach you all Questions in easy way. We solve all chapter wise sums of maths textbook. In every chapter include NCERT solutions. For solutions of Exercise 13.1, 13.2, 13.3, 13.4, 13.5, 13.6, 13.7, 13.8, 13.9 click on Tabs :
Question 1.
A plastic box 1.5 m long, 1.25 m wide and 65 cm deep is to be made. It is opened at the top. Ignoring the thickness of the plastic sheet, determine
(i) The area of the sheet required for making the box.
(ii) The cost of sheet for it, if a sheet measuring 1m2 costs ₹20.
Solution:
(i) Here, length (l) = 1.5 m, bread th(b) = 1 .25 m
and height (h) = 65 cm = 65/100 m = 0.65 m
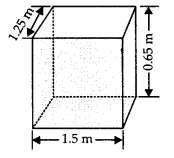
∵ It is open from the top.
∴ Its surface area
= [Lateral surface area] + [Base area]
= [2(1 + b)h] + [lb]
= [2(1.50 + 1.25)0.65] m2 + [1.50 x 1.25] m2
= [2 x 2.75 x 0.65] m2 + [1.875] m2
= 3.575 m2+ 1.875 m2 = 5.45 m2
∴ Area of the sheet required for making the box = 5.45 m2
(ii) Cost of 1 m2 sheet = Rs. 20
Cost of 5.45 m2 sheet = Rs. (20 x 5.45)
= Rs. 109
Hence, cost of the required sheet = Rs. 109
Question 2.
The length, breadth and height of a room are 5 m, 4 m and 3 m, respectively. Find the cost of white washing the walls of the room and the ceiling at the rate of ₹17.50 per m2.
Solution:
Length of the room (l) = 5 m
Breadth of the room (b) = 4 m
Height of the room (h) = 3 m
The room is like a cuboid whose four walls (lateral surface) and ceiling are to be white washed.
∴ Area for white washing
= [Lateral surface area] + [Area of the ceiling]
= [2(l + b)h] + [l x b]
= [2(5 + 4) x 3] m2 + [5 x 4] m2 = 54 m2 + 20 m2 = 74 m2
Cost of white washing for 1 m2 area = Rs. 7.50
∴ Cost of white washing for 74 m2 area = Rs. (7.50 x 74) = Rs. 555
Thus, the required cost of white washing = Rs. 555
Question 3.
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of ₹10 per m2 is ₹15000, find the height of the hall.
[Hint: Area of the four walls = Lateral surface area]
Solution:
A rectangular hall means a cuboid.
Let the length and breadth of the hall be l and b respectively.
∴ Perimeter of the floor = 2(l + b)
⇒ 2(l + b) = 250 m
∵ Area of four walls = Lateral surface area = 2(1 + b) x h, where h is the height of the hall = 250 h m2
Cost of painting the four walls
= Rs. (10 x 250 h) = Rs. 2500h
⇒ 2500 h = 15000 ⇒ h = 15000/2500 = 6
Thus, the required height of the hall = 6 m
Question 4.
The paint in a certain container is sufficient to paint an area equal to 9.375 m2. How many bricks of dimensions 22.5 cm x 10 cm x 7.5 cm can be painted out of this container.
Solution:
Total area that can be painted = 9.375 m2
Here, Length of a brick (l) = 22.5 cm
Breadth of a brick (b) = 10 cm
Height of a brick (h) = 7.5 cm
Since a brick is like a cuboid, then
Total surface area of a brick = 2[lb + bh + hl]
= 2[(225 x 1(0) + (10 x 7.5) + (7.5 x 22.5)] cm2
= 2[(225) + (75) + (168.75)] cm2
= 2[468.75] cm2 = 937.5 cm2 = 937.5/10000 m2
Let the required number of bricks be n
∴ Total surface area of n bricks = n x 937.5/10000 m2
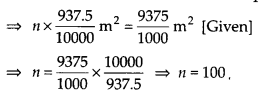
Thus, the required number of bricks = 100
Question 5.
A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.
(i) Which box has the greater lateral surface area and by how much?
(ii) Which box has the smaller total surface area and by how much?
Solution:
For the cubical box with edge (a) = 10 cm
Lateral surface area = 4a2 = 4 x 102 cm2
= 400 cm2
Total surface area = 6a2 = 6 x 102 cm2
= 600 cm2
For the cuboidal box with dimensions,
Length (l) = 12.5 cm,
Breadth (b) = 10 cm,
Height (h) = 8 cm
∴ Lateral surface area = 2[l + b] x h = 2[12.5 + 10] x 8 cm2 = 360 cm2
Total surface area = 2[lb + bh + hl]
= 2[(12.5 x 10) + (10 x 8) + (8 x 12.5)] cm2
= 2[125 + 80 + 100] cm2
= 2[305] cm2
= 610 cm2
(i) A cubical box has the greater lateral surface area by (400 – 360) cm2 = 40 cm2.
(ii) Total surface area of a cubical box is smaller than the cuboidal box by (610 – 600) cm2 = 10 cm2.
Question 6.
A small indoor greenhouse (herbarium) is made entirely of glass panes (including base) held together with tape. It is 30 cm long, 25 cm wide and 25 cm high.
(i) What is the area of the glass?
(ii) How much of tape is needed for all the 12 edges?
Solution:
The herbarium is like a cuboid.
Here, length (l) = 30 cm,
breadth (b) = 25 cm,
height (h) = 25 cm
(i) Surface area of the herbarium (glass)
= 2[lb + bh + hl]
= 2[(30 x 25) + (25 x 25) + (25 x 30)] cm2 – 2[750 + 625 + 750] cm2
= 2[2125] cm2
= 4250 cm2
Thus, the required area of the glass = 4250 cm2
(ii) Total length of 12 edges = 4l + 4b + 4h
= 4(l + b + h)
= 4(30 + 25 + 25) cm
= 4 x 80 cm = 320 cm
Thus, the required length of tape = 320 cm
Question 7.
Shanti Sweets Stalll was placing an order for making cardboard boxes for packing their sweets. Two sizes of boxes were required. The bigger of dimensions 25 cm x 20 cm x 5 cm and the smaller of dimensions 15 cm x 12 cm x 5 cm. For all the overlaps, 5% of the total surface area is required extra. If the cost of the cardboard is ₹4 for 1000 cm², find the cost of cardboard required for supplying 250 boxes of each kind.
Solution:
For bigger box:
Length (l) = 25 cm,
Breadth (b) = 20 cm,
Height (h) = 5 cm
Total surface area of a box = 2(lb + bh + hl)
= 2[(25 x 20) + (20 x 5) + (5 x t25)] cm2
= 2 [500 + 100 + 125] cm2
= 2[725] cm2
= 1450 cm2
Total surface area of 250 boxes = (250 x 1450) cm2 = 362500 cm2
For smaller box:
l = 15 cm, b = 12 cm, h = 5 cm
Total surface area of a box = 2 [lb + bh + hl]
= 2[(15 x 12) + (12 x 5) + (5 x 15)] cm2
= 2[180 + 60 + 75] cm2 = 2[315] cm2 = 630 cm2
∴ Total surface area of 250 boxes = (250 x 630) cm2 = 157500 cm2
Now, total surface area of both type of boxes = 362500 cm2 +157500 cm2 = 520000 cm2 Area for overlaps = 5% of [total surface area]
= 5/100 x 520000 cm2 = 26000 cm2
∴ Total surface area of the cardboard required = [Total surface area of 250 boxes of each type] + [Area for overlaps]
= 520000 cm2 + 26000 cm2 = 546000 cm2
∵ Cost of 1000 cm2 cardboard = Rs. 4
∴ Cost of 546000 cm2 cardboard
= Rs.4×546000/1000 = Rs. 2184
Question 8.
Parveen wanted to make a temporary shelter, for her car, by making a box-like structure with tarpaulin that covers all the four sides and the top of the car (with the front face as a flap which can be rolled up). Assuming that the stitching margins are very small and therefore negligible, how much tarpaulin would be required to make the shelter of height 2.5 m, with base dimensions 4 m x 3 m?
Solution:
Here, length (l) = 4 m,
breadth (b) = 3m
and height (h) = 2.5 m
The structure is like a cuboid.
∴ The surface area of the cuboid, excluding the base
=[Lateral surface area] + [Area of ceiling]
= [2(l + b)h] + [lb]
= [2(4 + 3) x 2.5] m2 + [4 x 3] m2
= 35 m2 + 12 m2 = 47 m2
Thus, 47 m2 tarpaulin would be required.
Question 1.
The curved surface area of a right circular cylinder of height 14 cm is 88 cm2. Find the diameter of the base of the cylinder.
Solution:
Let r be the radius of the cylinder.
Here, height (h) = 14 cm and curved surface area = 88 cm2
Curved surface area of a cylinder = 2πrh
⇒ 2πrh = 88
⇒ 2 x 22/7 x r x 14 = 88
⇒ r = 88×7/2×22×14 = 1 cm
∴ Diameter = 2 x r = (2 x 1) cm = 2 cm
Question 2.
It is required to make a closed cylindrical tank of height 1 m and base diameter 140 cm from a metal sheet. How many square metres of the sheet are required for the same?
Solution:
Here, height (h) = 1 m
Diameter of the base = 140 cm = 1.40 m
Radius (r) = 1.40/2m = 0.70 m
Total surface area of the cylinder = 2πr (h + r)
= 2 x 22/7 x 0.70(1 + 0.70)m2
= 2 x 22 x 0.10 x 1.70 m2
= 2 x 22 x 10/100 x 170/100m2
= 748/100m2 = 7.48 m2
Hence, the required sheet = 7.48 m2
Question 3.
A metal pipe is 77 cm long. The inner ft diameter of a cross section is 4 cm, the outer diameter being 4.4 cm (see figure). Find its
(i) inner curved surface area.
(ii) outer curved surface area.
(iii) total surface area.
Solution:
Length of the metal pipe = 77 cm
It is in the form of a cylinder.
∴ Height of the cylinder (h) = 77 cm
Inner diameter = 4 cm
Inner radius (r) = 4/2 cm = 2 cm
Outer diameter = 4.4 cm
⇒ Outer radius (R) = 4.4/2 cm = 2.2 cm
(i) Inner curved surface area = 2πrh
= 2 x 22/7 x 2 x 77 cm2
= 2 x 22 x 2 x 11 cm2 = 968 cm2
(ii) Outer curved surface area = 2πRh
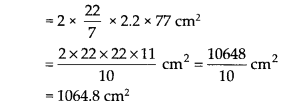
(iii)Total surface area = [Inner curved surface area] + [Outer curved surface area] + [Area of two circular ends]
= [2πrh] + [2πRh] + 2[π(R2 – r2)]
= [968 cm2] + [1064.8 cm2]
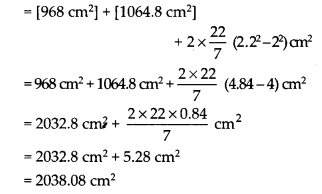
Question 4.
The diameter of a roller is 84 cm and its length is 120 cm. It takes 500 complete revolutions to move once over to level a playground. Find the area of the playground in m2.
Solution:
The roller is in the form of a cylinder of diameter = 84 cm
⇒ Radius of the roller(r) = 84/2 cm = 42 cm
Length of the roller (h) = 120 cm
Curved surface area of the roller = 2πrh
= 2 x 22/7 x 42 x 120 cm2
= 2 x 22 x 6 x 120 cm2 = 31680 cm2
Now, area of the playground levelled in one revolution of the roller = 31680 cm2
= 31680/10000m2
∴ Area of the playground levelled in 500
revolutions = 500 x 31680/10000m2 = 1584m2
Question 5.
A cylindrical pillar is 50 cm in diameter and 3.5 m in height. Find the cost of painting the curved surface of the pillar at the rate of ₹12.50 per m2 .
Solution:
Diameter of the pillar = 50 cm
∴ Radius (r) = 50/2m = 25 m = 1/4m
and height (h) = 3.5m
Curved surface area of a pillar = 2πrh
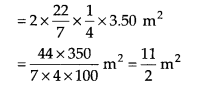
∴ Curved surface area to be painted = 11/2m2
∴ Cost of painting of 1 m2 pillar = Rs. 12.50
∴ Cost of painting of 11/2 m2 pillar
= Rs. ( 11/2 x 12.50 )
= Rs. 68.75.
Question 6.
Curved surface area of a right circular cylinder is 4.4 m2. If the radius of the base of the cylinder is 0.7 m, find its height.Curved surface area of a right circular cylinder is 4.4 m2. If the radius of the base of the cylinder is 0.7 m, find its height.
Solution:
Radius (r) = 0.7 m
Let height of the cylinder be h m
Curved surface area of a cylinder = 2πrh
= 2 x 22/7 x 7/10 x hm2
But the curved surface area is 4.4 m2. [Given]
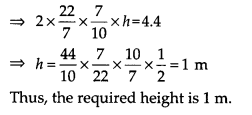
Question 7.
he inner diameter of a circular well is 3.5 m. It is 10 m deep. Find
(i) its inner curved surface area.
(ii) the cost of plastering this curved surface at the rate of ₹40 per m2.
Solution:
Hans Inner diameter of the well = 3.5 m
Radius of the well (r) = 3.5/2
Height of the well (h) = 10 m
(i) Inner curved surface area = 2πrh
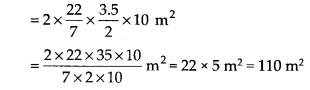
(ii) Cost of plastering per m2 = Rs. 40
∴ Total cost of plastering the area 110 m2
= Rs. (110 x 40) = Rs. 4400
Question 8.
In a hot water heating system, there is a cylindrical pipe of length 28 m and diameter 5 cm. Find the total radiating surface in the system.
Solution:
USD Length of the cylindrical pipe (h) = 28 m
Diameter of the pipe = 5 cm
∴ Radius (r) = 5/2 cm = 5/200 m
Curved surface area of a cylinder = 2πrh
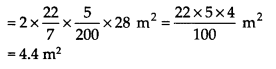
Thus, the total radiating surface is 4.4 m2 .
Question 9.
Find
(i) the lateral or curved surface area of a closed cylindrical petrol storage tank that is 4.2 m in diameter and 4.5 m high.
(ii) how much steel was actually used, if 1/12 of the steel actually used was wasted in making the tank.
Solution:
The storage tank is in the form of a cylinder.
∴ Diameter of the tank = 4.2 m
Radius (r) = 4.2/2 = 2.1 m
Height (h) = 4.5 m
Now,
(i) Lateral (or curved) surface area of the tank = 2πrh
= 2 x 22/7 x 2.1 x 4.5 m2
= 2 x 22 x 0.3 x 4.5 m2 59.4 m2
(ii) Total surface area of the tank = 2πr(r + h)
= 2 x 22/7 x 2.1(2.1 + 4.5)m2
= 44 x 0.3 x 6.6 m2 = 87.13 m2
Let actual area of the steel used be x m2
∴ Area of steel that was wasted = 1/12 x m2
= x/12m2
Area of steel used = x – x/12 m2
![]()
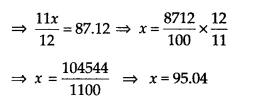
Thus, the required area of the steel that was actually used is 95.04 m2.
Question 10.
In figure, you see the frame of a lampshade. It is to be covered with a decorative cloth. The frame has a base diameter of 20 cm and height of 30 cm. A margin of 2.5 cm is to be given for folding it over the top and bottom of the frame. Find how much cloth is required for covering the lampshade.
Solution:
The lampshade is in the form of a cylinder,
where radius (r) = 20/2 cm = 10 cm
and height = 30 cm.
A margin of 2.5 cm is to be added to the top and bottom of the frame.
∴ Total height of the cylinder, (h)
= 30 cm + 2.5 cm + 2.5 cm = 35 cm
Now, curved surface area = 2πrh
= 2 x 22/7 x 10 x 35 cm2
= 2200 cm2
Thus, the required area of the cloth = 2200 cm2
Question 11.
The students of a Vidyalaya were asked to participate in a competition for making and decorating penholders in the shape of a cylinder with a base, using cardboard. Each penholder was to be of radius 3 cm and height 10.5 cm. The Vidyalaya was to supply the competitors with cardboard. If there were 35 competitors, how much cardboard was required to be bought for the competition?
Solution:
Here, the penholders are in the form of cylinder.
Radius of a penholder (r) = 3 cm
Height of a penholder (h) = 10.5 cm
Since, a penholder must be open from the top.
Now, surface area of a penholder = [Lateral surface area] + [Base area]
= [2πrh] + [πr2]
![]()
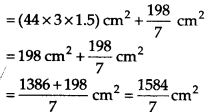
∴ Surface area of 35 penholders
= 35 x 1584/7 cm2 = 7920 cm2
Thus, 7920 cm2 of cardboard was required to be bought.
Question 1.
Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
Solution:
Here, diameter of the base = 10.5 cm
⇒ Radius (r) = 10.5/2 cm
and slant height (l) =10 cm
Curved surface area of the cone = πrl
= 22/7 x 10.5/2 x 10cm2
= 11 x 15 x 1 cm2 = 165cm2
Question 2.
Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
Solution:
Here, diameter = 24 m 24
∴ Radius (r) = 24/2 m = 12 m
and slant height (l) = 21 m
∴ Total surface area of a cone = πr(r +1)
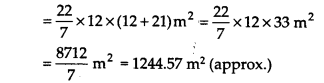
Question 3.
Curved surface area of a cone is 308 cm² and its slant height is 14 cm. Find
(i) radius of the base and
(ii) total surface area of the cone.
Solution:
Here, curved surface area = πrl = 308 cm2
Slant height (l) = 14 cm
(i) Let the radius of the base be ‘r’ cm
∴ πrl = 308 ⇒ 22/7 x r x 14 = 308
r = 308×7/22×14 = 7cm
Thus, radius of the cone is 7 cm
(ii) Base area = πr2 = 22/7 x 72 cm2
= 22 x 7 cm2 = 154 cm2
and curved surface area = 308 cm2 [Given]
∴ Total surface area of the cone
= [Curved surface area] + [Base area] = 308 cm2 + 154 cm2
= 462 cm2
Question 4.
A conical tent is 10 m high and the radius of its base is 24 m. Find
(i) slant height of the tent.
(ii) cost of the canvas required to make the tent, if the cost of 1 m2 canvas is ₹70.
Solution:
Here, height of the tent (h) = 10 m
Radius of the base (r) = 24 m
(i) The slant height, l =
(i) In right triangle ABO, we have
AB2 = AO2+BO2(using Pythagoras theorem)
l2 = h2+r2
= (10)2+(24)2
= 676
l = 26
Therefore, the slant height of the tent is 26 m.
(ii) CSA of tent = πrl
= (22/7)×24×26 m2
Cost of 1 m2 canvas = Rs 70
Cost of (13728/7)m2 canvas is equal to Rs (13728/7)×70 = Rs 137280
Therefore, the cost of the canvas required to make such a tent is Rs 137280.
5. What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm. [Use π=3.14]
Solution:
Height of conical tent, h = 8m
Radius of base of tent, r = 6m
Slant height of tent, l2 = (r2+h2)
l2 = (62+82) = (36+64) = (100)
or l = 10
Again, CSA of conical tent = πrl
= (3.14×6×10) m2
= 188.4m2
Let the length of tarpaulin sheet required be L
As 20 cm will be wasted, therefore,
Effective length will be (L-0.2m).
Breadth of tarpaulin = 3m (given)
Area of sheet = CSA of tent
[(L–0.2)×3] = 188.4
L-0.2 = 62.8
L = 63
Therefore, the length of the required tarpaulin sheet will be 63 m.
6. The slant height and base diameter of conical tomb are 25m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of Rs. 210 per 100 m2. (Assume π = 22/7)
Solution:
Slant height of conical tomb, l = 25m
Base radius, r = diameter/2 = 14/2 m = 7m
CSA of conical tomb = πrl
= (22/7)×7×25 = 550
CSA of conical tomb= 550m2
Cost of white-washing 550 m2 area, which is Rs (210×550)/100
= Rs. 1155
Therefore, cost will be Rs. 1155 while white-washing tomb.
7. A joker’s cap is in the form of right circular cone of base radius 7 cm and height 24cm. Find the area of the sheet required to make 10 such caps. (Assume π =22/7)
Solution:
Radius of conical cap, r = 7 cm
Height of conical cap, h = 24cm
Slant height, l2 = (r2+h2)
= (72+242)
= (49+576)
= (625)
Or l = 25 cm
CSA of 1 conical cap = πrl
= (22/7)×7×24
= 550
CSA of 10 caps = (10×550) cm2 = 5500 cm2
Therefore, the area of the sheet required to make 10 such caps is 5500 cm2.
8. A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is Rs. 12 per m2, what will be the cost of painting all these cones? (Use π = 3.14 and take √(1.04) =1.02)
Solution:
Given:
Radius of cone, r = diameter/2 = 40/2 cm = 20cm = 0.2 m
Height of cone, h = 1m
Slant height of cone is l, and l2 = (r2+h2)
Using given values, l2 = (0.22+12)
= (1.04)
Or l = 1.02
Slant height of the cone is 1.02 m
Now,
CSA of each cone = πrl
= (3.14×0.2×1.02)
= 0.64056
CSA of 50 such cones = (50×0.64056) = 32.028
CSA of 50 such cones = 32.028 m2
Again,
Cost of painting 1 m2 area = Rs 12 (given)
Cost of painting 32.028 m2 area = Rs (32.028×12)
= Rs.384.336
= Rs.384.34 (approximately)
Therefore, the cost of painting all these cones is Rs. 384.34.
1. Find the surface area of a sphere of radius:
(i) 10.5cm (ii) 5.6cm (iii) 14cm
(Assume π=22/7)
Solution:
Formula: Surface area of sphere (SA) = 4πr2
(i) Radius of sphere, r = 10.5 cm
SA = 4×(22/7)×10.52 = 1386
Surface area of sphere is 1386 cm2
(ii) Radius of sphere, r = 5.6cm
Using formula, SA = 4×(22/ 7)×5.62 = 394.24
Surface area of sphere is 394.24 cm2
(iii) Radius of sphere, r = 14cm
SA = 4πr2
= 4×(22/7)×(14)2
= 2464
Surface area of sphere is 2464 cm2
2. Find the surface area of a sphere of diameter:
(i) 14cm (ii) 21cm (iii) 3.5cm
(Assume π = 22/7)
Solution:
(i) Radius of sphere, r = diameter/2 = 14/2 cm = 7 cm
Formula for Surface area of sphere = 4πr2
= 4×(22/7)×72 = 616
Surface area of a sphere is 616 cm2
(ii) Radius (r) of sphere = 21/2 = 10.5 cm
Surface area of sphere = 4πr2
= 4×(22/7)×10.52 = 1386
Surface area of a sphere is 1386 cm2
Therefore, the surface area of a sphere having diameter 21cm is 1386 cm2
(iii) Radius(r) of sphere = 3.5/2 = 1.75 cm
Surface area of sphere = 4πr2
= 4×(22/7)×1.752 = 38.5
Surface area of a sphere is 38.5 cm2
3. Find the total surface area of a hemisphere of radius 10 cm. [Use π=3.14]
Solution:
Radius of hemisphere, r = 10cm
Formula: Total surface area of hemisphere = 3πr2
= 3×3.14×102 = 942
The total surface area of given hemisphere is 942 cm2.
4. The radius of a spherical balloon increases from 7cm to 14cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
Solution:
Let r1 and r2 be the radii of spherical balloon and spherical balloon when air is pumped into it respectively. So
r1 = 7cm
r2 = 14 cm
Now, Required ratio = (initial surface area)/(Surface area after pumping air into balloon)
= 4r12/4r22
= (r1/r2)2
= (7/14)2 = (1/2)2 = ¼
Therefore, the ratio between the surface areas is 1:4.
5. A hemispherical bowl made of brass has inner diameter 10.5cm. Find the cost of tin-plating it on the inside at the rate of Rs 16 per 100 cm2. (Assume π = 22/7)
Solution:
Inner radius of hemispherical bowl, say r = diameter/2 = (10.5)/2 cm = 5.25 cm
Formula for Surface area of hemispherical bowl = 2πr2
= 2×(22/7)×(5.25)2 = 173.25
Surface area of hemispherical bowl is 173.25 cm2
Cost of tin-plating 100 cm2 area = Rs 16
Cost of tin-plating 1 cm2 area = Rs 16 /100
Cost of tin-plating 173.25 cm2 area = Rs. (16×173.25)/100 = Rs 27.72
Therefore, the cost of tin-plating the inner side of the hemispherical bowl at the rate of Rs 16 per 100 cm2 is Rs 27.72.
6. Find the radius of a sphere whose surface area is 154 cm2. (Assume π = 22/7)
Solution:
Let the radius of the sphere be r.
Surface area of sphere = 154 (given)
Now,
4πr2 = 154
r2 = (154×7)/(4×22) = (49/4)
r = (7/2) = 3.5
The radius of the sphere is 3.5 cm.
7. The diameter of the moon is approximately one fourth of the diameter of the earth.
Find the ratio of their surface areas.
Solution:
If diameter of earth is said d, then the diameter of moon will be d/4 (as per given statement)
Radius of earth = d/2
Radius of moon = ½×d/4 = d/8
Surface area of moon = 4π(d/8)2
Surface area of earth = 4π(d/2)2

The ratio between their surface areas is 1:16.
8. A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5cm. Find the outer curved surface of the bowl. (Assume π =22/7)
Solution:
Given:
Inner radius of hemispherical bowl = 5cm
Thickness of the bowl = 0.25 cm
Outer radius of hemispherical bowl = (5+0.25) cm = 5.25 cm
Formula for outer CSA of hemispherical bowl = 2πr2, where r is radius of hemisphere
= 2×(22/7)×(5.25)2 = 173.25
Therefore, the outer curved surface area of the bowl is 173.25 cm2.
9. A right circular cylinder just encloses a sphere of radius r (see fig. 13.22). Find
(i) surface area of the sphere,
(ii) curved surface area of the cylinder,
(iii) ratio of the areas obtained in(i) and (ii).
Solution:
(i) Surface area of sphere = 4πr2, where r is the radius of sphere
(ii) Height of cylinder, h = r+r =2r
Radius of cylinder = r
CSA of cylinder formula = 2πrh = 2πr(2r) (using value of h)
= 4πr2
(iii) Ratio between areas = (Surface area of sphere)/CSA of Cylinder)
= 4r2/4r2 = 1/1
Ratio of the areas obtained in (i) and (ii) is 1:1.
1. A matchbox measures 4 cm×2.5cm×1.5cm. What will be the volume of a packet containing 12 such boxes?
Solution:
Dimensions of a matchbox (a cuboid) are l×b×h = 4 cm×2.5 cm×1.5 cm respectively
Formula to find the volume of matchbox = l×b×h = (4×2.5×1.5) = 15
Volume of matchbox = 15 cm3
Now, volume of 12 such matchboxes = (15×12) cm3 = 180 cm3
Therefore, the volume of 12 matchboxes is 180cm3.
2. A cuboidal water tank is 6m long, 5m wide and 4.5m deep. How many litres of water can it hold? (1 m3= 1000 l)
Solution:
Dimensions of a cuboidal water tank are: l = 6 m and b = 5 m and h = 4.5 m
Formula to find volume of tank, V = l×b×h
Put the values, we get
V = (6×5×4.5) = 135
Volume of water tank is 135 m3
Again,
We are given that, amount of water that 1m3 volume can hold = 1000 l
Amount of water, 135 m3volume hold = (135×1000) litres = 135000 litres
Therefore, given cuboidal water tank can hold up to135000 litres of water.
3. A cuboidal vessel is 10m long and 8m wide. How high must it be made to hold 380 cubic metres of a liquid?
Solution:
Given:
Length of cuboidal vessel, l = 10 m
Width of cuboidal vessel, b = 8m
Volume of cuboidal vessel, V = 380 m3
Let the height of the given vessel be h.
Formula for Volume of a cuboid, V = l×b×h
Using formula, we have
l×b×h = 380
10×8×h= 380
Or h = 4.75
Therefore, the height of the vessels is 4.75 m.
4. Find the cost of digging a cuboidal pit 8m long, 6m broad and 3m deep at the rate of Rs 30 per m3.
Solution:
The given pit has its length(l) as 8m, width (b)as 6m and depth (h)as 3 m.
Volume of cuboidal pit = l×b×h = (8×6×3) = 144 (using formula)
Required Volume is 144 m3
Now,
Cost of digging per m3 volume = Rs 30
Cost of digging 144 m3 volume = Rs (144×30) = Rs 4320
5. The capacity of a cuboidal tank is 50000 litres of water. Find the breadth of the tank, if its length and depth are respectively 2.5 m and 10 m.
Solution:
Length (l) and depth (h) of tank is 2.5 m and 10 m respectively.
To find: The value of breadth, say b.
Formula to find the volume of a tank = l×b×h = (2.5× b×10) m3= 25b m3
Capacity of tank= 25b m3, which is equal to 25000b litres
Also, capacity of a cuboidal tank is 50000 litres of water (Given)
Therefore, 25000 b = 50000
This implies, b = 2
Therefore, the breadth of the tank is 2 m.
6. A village, having a population of 4000, requires 150 litres of water per head per day.
It has a tank measuring 20 m×15 m×6 m. For how many days will the water of this tank last?
Solution:
Length of the tank = l = 20 m
Breadth of the tank = b = 15 m
Height of the tank = h = 6 m
Total population of a village = 4000
Consumption of the water per head per day = 150 litres
Water consumed by the people in 1 day = (4000×150) litres = 600000 litres …(1)
Formula to find the capacity of tank, C = l×b×h
Using given data, we have
C = (20×15×6) m3= 1800 m3
Or C = 1800000 litres
Let water in this tank last for d days.
Water consumed by all people in d days = Capacity of tank (using equation (1))
600000 d =1800000
d = 3
Therefore, the water of this tank will last for 3 days. Answer
7. A godown measures 40 m×25m×15 m. Find the maximum number of wooden crates each
measuring 1.5m×1.25 m×0.5 m that can be stored in the godown.
Solution:
From statement, we have
Length of the godown = 40 m
Breadth = 25 m
Height = 15 m
Whereas,
Length of the wooden crate = 1.5 m
Breadth = 1.25 m
Height = 0.5 m
Since godown and wooden crate are in cuboidal shape. Find the volume of each using formula, V = lbh.
Now,
Volume of godown = (40×25×15) m3 = 15000 m3
Volume of a wooden crate = (1.5×1.25×0.5) m3 = 0.9375 m3
Let us consider that, n wooden crates can be stored in the godown, then
Volume of n wooden crates = Volume of godown
0.9375×n =15000
Or n= 15000/0.9375 = 16000
Hence, the number of wooden crates that can be stored in the godown is 16,000.
8. A solid cube of side 12 cm is cut into eight cubes of equal volume. What will be the side of the new cube? Also, find the ratio between their surface areas.
Solution:
Side of a cube = 12cm (Given)
Find the volume of cube:
Volume of cube = (Side)3 = (12)3cm3= 1728cm3
Surface area of a cube with side 12 cm = 6a2 = 6(12) 2 cm2 …(1)
Cube is cut into eight small cubes of equal volume, say side of each cube is p.
Volume of a small cube = p3
Surface area = 6p2 …(2)
Volume of each small cube = (1728/8) cm3 = 216 cm3
Or (p)3 = 216 cm3
Or p = 6 cm
Now, Surface areas of the cubes ratios = (Surface area of bigger cube)/(Surface area of smaller cubes)
From equation (1) and (2), we get
Surface areas of the cubes ratios = (6a2)/(6p2) = a2/p2 = 122/62 = 4
Therefore, the required ratio is 4 : 1.
9. A river 3m deep and 40m wide is flowing at the rate of 2km per hour. How much water will fall into the sea in a minute?
Solution:
Given:
Depth of river, h = 3 m
Width of river, b = 40 m
Rate of water flow = 2km per hour = 2000m/60min = 100/3 m/min
Now, Volume of water flowed in 1 min = (100/3) × 40 × 3 = 4000m3
Therefore, 4000 m3water will fall into the sea in a minute.
1. The circumference of the base of cylindrical vessel is 132cm and its height is 25cm.
How many litres of water can it hold? (1000 cm3= 1L) (Assume π = 22/7)
Solution:
Circumference of the base of cylindrical vessel = 132 cm
Height of vessel, h = 25 cm
Let r be the radius of the cylindrical vessel.
Step 1: Find the radius of vessel
We know that, circumference of base = 2πr, so
2πr = 132 (given)
r = (132/(2 π))
r = 66×7/22 = 21
Radius is 21 cm
Step 2: Find the volume of vessel
Formula: Volume of cylindrical vessel = πr2h
= (22/7)×212×25
= 34650
Therefore, volume is 34650 cm3
Since, 1000 cm3 = 1L
So, Volume = 34650/1000 L= 34.65L
Therefore, vessel can hold 34.65 litres of water.
2. The inner diameter of a cylindrical wooden pipe is 24cm and its outer diameter is 28 cm. The length of the pipe is 35cm.Find the mass of the pipe, if 1cm3 of wood has a mass of 0.6g. (Assume π = 22/7)
Solution:
Inner radius of cylindrical pipe, say r1 = diameter1/ 2 = 24/2 cm = 12cm
Outer radius of cylindrical pipe, say r2 = diameter2/ 2 = 28/2 cm = 14 cm
Height of pipe, h = Length of pipe = 35cm
Now, the Volume of pipe = π(r22-r12)h cm3
Substitute the values.
Volume of pipe = 110×52 cm3 = 5720 cm3
Since, Mass of 1 cm3 wood = 0.6 g
Mass of 5720 cm3 wood = (5720×0.6) g = 3432 g or 3.432 kg. Answer!
3. A soft drink is available in two packs – (i) a tin can with a rectangular base of length 5cm and width 4cm, having a height of 15 cm and (ii) a plastic cylinder with circular base of diameter 7cm and height 10cm. Which container has greater capacity and by how much? (Assume π=22/7)
Solution:
- tin can will be cuboidal in shape
Dimensions of tin can are
Length, l = 5 cm
Breadth, b = 4 cm
Height, h = 15 cm
Capacity of tin can = l×b×h= (5×4×15) cm3 = 300 cm3
- Plastic cylinder will be cylindrical in shape.
Dimensions of plastic can are:
Radius of circular end of plastic cylinder, r = 3.5cm
Height , H = 10 cm
Capacity of plastic cylinder = πr2H
Capacity of plastic cylinder = (22/7)×(3.5)2×10 = 385
Capacity of plastic cylinder is 385 cm3
From results of (i) and (ii), plastic cylinder has more capacity.
Difference in capacity = (385-300) cm3 = 85cm3
4. If the lateral surface of a cylinder is 94.2cm2 and its height is 5cm, then find
(i) radius of its base (ii) its volume.[Use π= 3.14]
Solution:
CSA of cylinder = 94.2 cm2
Height of cylinder, h = 5cm
(i) Let radius of cylinder be r.
Using CSA of cylinder, we get
2πrh = 94.2
2×3.14×r×5 = 94.2
r = 3
radius is 3 cm
(ii) Volume of cylinder
Formula for volume of cylinder = πr2h
Now, πr2h = (3.14×(3)2×5) (using value of r from (i))
= 141.3
Volume is 141.3 cm3
5. It costs Rs 2200 to paint the inner curved surface of a cylindrical vessel 10m deep. If the cost of painting is at the rate of Rs 20 per m2, find
(i) inner curved surface area of the vessel
(ii) radius of the base
(iii) capacity of the vessel
(Assume π = 22/7)
Solution:
(i) Rs 20 is the cost of painting 1 m2 area.
Rs 1 is the cost to paint 1/20 m2 area
So, Rs 2200 is the cost of painting = (1/20×2200) m2
= 110 m2 area
The inner surface area of the vessel is 110m2.
(ii) Radius of the base of the vessel, let us say r.
Height (h) = 10 m and
Surface area formula = 2πrh
Using result of (i)
2πrh = 110 m2
2×22/7×r×10 = 110
r = 1.75
Radius is 1.75 m.
(iii) Volume of vessel formula = πr2h
Here r = 1.75 and h = 10
Volume = (22/7)×(1.75)2×10 = 96.25
Volume of vessel is 96.25 m3
Therefore, the capacity of the vessel is 96.25 m3 or 96250 litres.
6. The capacity of a closed cylindrical vessel of height 1m is15.4 liters. How many square meters of metal sheet would be needed to make it? (Assume π = 22/7)
Solution:
Height of cylindrical vessel, h = 1 m
Capacity of cylindrical vessel = 15.4 litres = 0.0154 m3
Let r be the radius of the circular end.
Now,
Capacity of cylindrical vessel = (22/7)×r2×1 = 0.0154
After simplifying, we get, r = 0.07 m
Again, total surface area of vessel = 2πr(r+h)
= 2×22/7×0.07(0.07+1)
= 0.44×1.07
= 0.4708
Total surface area of vessel is 0.4708 m2
Therefore, 0.4708 m2 of the metal sheet would be required to make the cylindrical vessel.
7. A lead pencil consists of a cylinder of wood with solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of the pencil is 14 cm, find the volume of the wood and that of the graphite. (Assume π = 22/7)
Solution:
Radius of pencil, r1 = 7/2 mm = 0.7/2 cm = 0.35 cm
Radius of graphite, r2 = 1/2 mm = 0.1/2 cm = 0.05 cm
Height of pencil, h = 14 cm
Formula to find, volume of wood in pencil = (r12-r22)h cubic units
Substitute the values, we have
= [(22/7)×(0.352-0.052)×14]
= 44×0.12
= 5.28
This implies, volume of wood in pencil = 5.28 cm3
Again,
Volume of graphite = r22h cubic units
Substitute the values, we have
= (22/7)×0.052×14
= 44×0.0025
= 0.11
So, the volume of graphite is 0.11 cm3.
8. A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7cm. If the bowl is filled with soup to a height of 4cm, how much soup the hospital has to prepare daily to serve 250 patients? (Assume π = 22/7)
Solution:
Diameter of cylindrical bowl = 7 cm
Radius of cylindrical bowl, r = 7/2 cm = 3.5 cm
Bowl is filled with soup to a height of4cm, so h = 4 cm
Volume of soup in one bowl= πr2h
(22/7)×3.52×4 = 154
Volume of soup in one bowl is 154 cm3
Therefore,
Volume of soup given to 250 patients = (250×154) cm3= 38500 cm3
= 38.5litres. Ans.
1. Find the volume of the right circular cone with
(i) radius 6cm, height 7 cm (ii) radius 3.5 cm, height 12 cm (Assume π = 22/7)
Solution:
Volume of cone = (1/3) πr2h cube units
Where r be radius and h be the height of the cone
(i) Radius of cone, r = 6 cm
Height of cone, h = 7cm
Say, V be the volume of the cone, we have
V = (1/3)×(22/7)×36×7
= (12×22)
= 264
The volume of the cone is 264 cm3.
(ii) Radius of cone, r = 3.5cm
Height of cone, h = 12cm
Volume of cone = (1/3)×(22/7)×3.52×7 = 154
Hence,
The volume of the cone is 154 cm3.
2. Find the capacity in litres of a conical vessel with
(i) radius 7cm, slant height 25 cm (ii) height 12 cm, slant height 12 cm
(Assume π = 22/7)
Solution:
(i) Radius of cone, r =7 cm
Slant height of cone, l = 25 cm
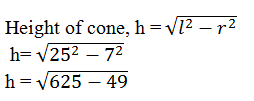
or h = 24
Height of the cone is 24 cm
Now,
Volume of cone, V = (1/3) πr2h (formula)
V = (1/3)×(22/7) ×72×24
= (154×8)
= 1232
So, the volume of the vessel is 1232 cm3
Therefore, capacity of the conical vessel = (1232/1000) liters (because 1L = 1000 cm3)
= 1.232 Liters.
(ii) Height of cone, h = 12 cm
Slant height of cone, l = 13 cm
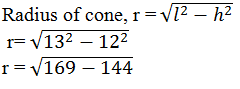
r = 5
Hence, the radius of cone is 5 cm.
Now, Volume of cone, V = (1/3)πr2h
V = (1/3)×(22/7)×52×12 cm3
= 2200/7
Volume of cone is 2200/7 cm3
Now, Capacity of the conical vessel= 2200/7000 litres (1L = 1000 cm3)
= 11/35 litres
3. The height of a cone is 15cm. If its volume is 1570cm3, find the diameter of its base. (Use π = 3.14)
Solution:
Height of the cone, h = 15 cm
Volume of cone =1570 cm3
Let r be the radius of the cone
As we know: Volume of cone, V = (1/3) πr2h
So, (1/3) πr2h = 1570
(1/3)×3.14×r2 ×15 = 1570
r2 = 100
r = 10
Radius of the base of cone 10 cm.
4. If the volume of a right circular cone of height 9cm is 48πcm3, find the diameter of its base.
Solution:
Height of cone, h = 9cm
Volume of cone =48π cm3
Let r be the radius of the cone.
As we know: Volume of cone, V = (1/3) πr2h
So, 1/3 π r2(9) = 48 π
r2 = 16
r = 4
Radius of cone is 4 cm.
So, diameter = 2×Radius = 8
Thus, diameter of base is 8cm.
5. A conical pit of top diameter 3.5m is 12m deep. What is its capacity in kiloliters?
(Assume π = 22/7)
Solution:
Diameter of conical pit = 3.5 m
Radius of conical pit, r = diameter/ 2 = (3.5/2)m = 1.75m
Height of pit, h = Depth of pit = 12m
Volume of cone, V = (1/3) πr2h
V = (1/3)×(22/7) ×(1.75)2×12 = 38.5
Volume of cone is 38.5 m3
Hence, capacity of the pit = (38.5×1) kiloliters = 38.5 kiloliters.
6. The volume of a right circular cone is 9856cm3. If the diameter of the base is 28cm, find
(i) height of the cone
(ii) slant height of the cone
(iii) curved surface area of the cone
(Assume π = 22/7)
Solution:
Volume of a right circular cone = 9856 cm3
Diameter of the base = 28 cm
(i) Radius of cone, r = (28/2) cm = 14 cm
Let the height of the cone be h
Volume of cone, V = (1/3) πr2h
(1/3) πr2h = 9856
(1/3)×(22/7) ×14×14×h = 9856
h = 48
The height of the cone is 48 cm.
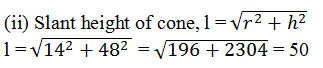
Slant height of the cone is 50 cm.
(iii) curved surface area of cone = πrl
= (22/7)×14×50
= 2200
curved surface area of the cone is 2200 cm2.
7. A right triangle ABC with sides 5cm, 12cm and 13cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
Solution:
Height (h)= 12 cm
Radius (r) = 5 cm, and
Slant height (l) = 13 cm
Volume of cone, V = (1/3) πr2h
V = (1/3)×π×52×12
= 100π
Volume of the cone so formed is 100π cm3.
8. If the triangle ABC in the Question 7 is revolved about the side 5cm, then find the volume of the solids so obtained. Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.
Solution:
A right-angled ΔABC is revolved about its side 5cm, a cone will be formed of radius as 12 cm, height as 5 cm, and slant height as 13 cm.
Volume of cone = (1/3) πr2h; where r is the radius and h be the height of cone
= (1/3)×π×12×12×5
= 240 π
The volume of the cones of formed is 240π cm3.
So, required ratio = (result of question 7) / (result of question 8) = (100π)/(240π) = 5/12 = 5:12.
9. A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas.
(Assume π = 22/7)
Solution:
Radius (r) of heap = (10.5/2) m = 5.25
Height (h) of heap = 3m
Volume of heap = (1/3)πr2h
= (1/3)×(22/7)×5.25×5.25×3
= 86.625
The volume of the heap of wheat is 86.625 m3.
Again,

Therefore, the area of the canvas is 99.825 m2.
1. Find the volume of a sphere whose radius is
(i) 7 cm (ii) 0.63 m
(Assume π =22/7)
Solution:
(i) Radius of sphere, r = 7 cm
Using, Volume of sphere = (4/3) πr3
= (4/3)×(22/7)×73
= 4312/3
Hence, volume of the sphere is 4312/3 cm3
(ii) Radius of sphere, r = 0.63 m
Using, volume of sphere = (4/3) πr3
= (4/3)×(22/7)×0.633
= 1.0478
Hence, volume of the sphere is 1.05 m3 (approx).
2. Find the amount of water displaced by a solid spherical ball of diameter
(i) 28 cm (ii) 0.21 m
(Assume π =22/7)
Solution:
(i) Diameter = 28 cm
Radius, r = 28/2 cm = 14cm
Volume of the solid spherical ball = (4/3) πr3
Volume of the ball = (4/3)×(22/7)×143 = 34496/3
Hence, volume of the ball is 34496/3 cm3
(ii) Diameter = 0.21 m
Radius of the ball =0.21/2 m= 0.105 m
Volume of the ball = (4/3 )πr3
Volume of the ball = (4/3)× (22/7)×0.1053 m3
Hence, volume of the ball = 0.004851 m3
3.The diameter of a metallic ball is 4.2cm. What is the mass of the ball, if the density of the metal is 8.9 g per cm3? (Assume π=22/7)
Solution:
Given,
Diameter of a metallic ball = 4.2 cm
Radius(r) of the metallic ball, r = 4.2/2 cm = 2.1 cm
Volume formula = 4/3 πr3
Volume of the metallic ball = (4/3)×(22/7)×2.1 cm3
Volume of the metallic ball = 38.808 cm3
Now, using relationship between, density, mass and volume,
Density = Mass/Volume
Mass = Density × volume
= (8.9×38.808) g
= 345.3912 g
Mass of the ball is 345.39 g (approx).
4. The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?
Solution:
Let the diameter of earth be “d”. Therefore, the radius of earth will be will be d/2
Diameter of moon will be d/4 and the radius of moon will be d/8
Find the volume of the moon :
Volume of the moon = (4/3) πr3 = (4/3) π (d/8)3 = 4/3π(d3/512)
Find the volume of the earth :
Volume of the earth = (4/3) πr3= (4/3) π (d/2)3 = 4/3π(d3/8)
Fraction of the volume of the earth is the volume of the moon


5. How many litres of milk can a hemispherical bowl of diameter 10.5cm hold? (Assume π = 22/7)
Solution:
Diameter of hemispherical bowl = 10.5 cm
Radius of hemispherical bowl, r = 10.5/2 cm = 5.25 cm
Formula for volume of the hemispherical bowl = (2/3) πr3
Volume of the hemispherical bowl = (2/3)×(22/7)×5.253 = 303.1875
Volume of the hemispherical bowl is 303.1875 cm3
Capacity of the bowl = (303.1875)/1000 L = 0.303 litres(approx.)
Therefore, hemispherical bowl can hold 0.303 litres of milk.
6. A hemi spherical tank is made up of an iron sheet 1cm thick. If the inner radius is 1 m, then find the volume of the iron used to make the tank. (Assume π = 22/7)
Solution:
Inner Radius of the tank, (r ) = 1m
Outer Radius (R ) = 1.01m
Volume of the iron used in the tank = (2/3) π(R3– r3)
Put values,
Volume of the iron used in the hemispherical tank = (2/3)×(22/7)×(1.013– 13) = 0.06348
So, volume of the iron used in the hemispherical tank is 0.06348 m3.
7. Find the volume of a sphere whose surface area is 154 cm2. (Assume π = 22/7)
Solution:
Let r be the radius of a sphere.
Surface area of sphere = 4πr2
4πr2 = 154 cm2 (given)
r2 = (154×7)/(4 ×22)
r = 7/2
Radius is 7/2 cm
Now,
Volume of the sphere = (4/3) πr3
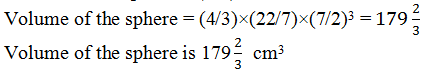
8. A dome of a building is in the form of a hemi sphere. From inside, it was white-washed at the cost of Rs. 4989.60. If the cost of white-washing isRs20 per square meter, find the
(i) inside surface area of the dome (ii) volume of the air inside the dome
(Assume π = 22/7)
Solution:
(i) Cost of white-washing the dome from inside = Rs 4989.60
Cost of white-washing 1m2 area = Rs 20
CSA of the inner side of dome = 498.96/2 m2 = 249.48 m2
(ii) Let the inner radius of the hemispherical dome be r.
CSA of inner side of dome = 249.48 m2 (from (i))
Formula to find CSA of a hemi sphere = 2πr2
2πr2 = 249.48
2×(22/7)×r2 = 249.48
r2 = (249.48×7)/(2×22)
r2 = 39.69
r = 6.3
So, radius is 6.3 m
Volume of air inside the dome = Volume of hemispherical dome
Using formula, volume of the hemisphere = 2/3 πr3
= (2/3)×(22/7)×6.3×6.3×6.3
= 523.908
= 523.9(approx.)
Answer: Volume of air inside the dome is 523.9 m3.
9. Twenty-seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S’. Find the
(i) radius r’ of the new sphere,
(ii) ratio of Sand S’.
Solution:
Volume of the solid sphere = (4/3)πr3
Volume of twenty seven solid sphere = 27×(4/3)πr3 = 36 π r3
(i) New solid iron sphere radius = r’
Volume of this new sphere = (4/3)π(r’)3
(4/3)π(r’)3 = 36 π r3
(r’)3 = 27r3
r’= 3r
Radius of new sphere will be 3r (thrice the radius of original sphere)
(ii) Surface area of iron sphere of radius r, S =4πr2
Surface area of iron sphere of radius r’= 4π (r’)2
Now
S/S’ = (4πr2)/( 4π (r’)2)
S/S’ = r2/(3r’)2 = 1/9
The ratio of S and S’ is 1: 9.
10. A capsule of medicine is in the shape of a sphere of diameter 3.5mm. How much medicine (in mm3) is needed to fill this capsule? (Assume π = 22/7)
Solution:
Diameter of capsule = 3.5 mm
Radius of capsule, say r = diameter/ 2 = (3.5/2) mm = 1.75mm
Volume of spherical capsule = 4/3 πr3
Volume of spherical capsule = (4/3)×(22/7)×(1.75)3 = 22.458
Answer: The volume of the spherical capsule is 22.46 mm3.
1. A wooden bookshelf has external dimensions as follows: Height = 110cm, Depth = 25cm,
Breadth = 85cm (see fig. 13.31). The thickness of the plank is 5cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2, find the total expenses required for polishing and painting the surface of the bookshelf.
Solution:
External dimensions of book self,
Length, l = 85cm
Breadth, b = 25 cm
Height, h = 110 cm
External surface area of shelf while leaving out the front face of the shelf
= lh+2(lb+bh)
= [85×110+2(85×25+25×110)] = (9350+9750) = 19100
External surface area of shelf is 19100 cm2
Area of front face = [85×110-75×100+2(75×5)] = 1850+750
So, area is 2600 cm2
Area to be polished = (19100+2600) cm2 = 21700 cm2.
Cost of polishing 1 cm2 area = Rs 0.20
Cost of polishing 21700 cm2 area Rs. (21700×0.20) = Rs 4340
Dimensions of row of the book shelf
Length(l) = 75 cm
Breadth (b) = 20 cm and
Height(h) = 30 cm
Area to be painted in one row= 2(l+h)b+lh = [2(75+30)× 20+75×30] = (4200+2250) = 6450
So, area is 6450 cm2.
Area to be painted in 3 rows = (3×6450)cm2 = 19350 cm2.
Cost of painting 1 cm2 area = Rs. 0.10
Cost of painting 19350 cm2 area = Rs (19350 x 0.1) = Rs 1935
Total expense required for polishing and painting = Rs. (4340+1935) = Rs. 6275
Answer: The cost for polishing and painting the surface of the book shelf is Rs. 6275.
2. The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in fig. 13.32. Eight such spheres are used forth is purpose, and are to be painted silver. Each support is a cylinder of radius 1.5cm and height 7cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per cm2 and black paint costs 5 paise per cm2.
Solution:
Diameter of wooden sphere = 21 cm
Radius of wooden sphere, r = diameter/ 2 = (21/2) cm = 10.5 cm
Formula: Surface area of wooden sphere = 4πr2
= 4×(22/7)×(10.5)2 = 1386
So, surface area is 1386 cm3
Radius of the circular end of cylindrical support = 1.5 cm
Height of cylindrical support = 7 cm
Curved surface area = 2πrh
= 2×(22/7)×1.5×7 = 66
So, CSA is 66 cm2
Now,
Area of the circular end of cylindrical support = πr2
= (22/7)×1.52
= 7.07
Area of the circular end is 7.07 cm2
Again,
Area to be painted silver = [8 ×(1386-7.07)] = 8×1378.93 = 11031.44
Area to be painted is 11031.44 cm2
Cost for painting with silver colour = Rs(11031.44×0.25) =Rs 2757.86
Area to be painted black = (8×66) cm2 = 528 cm2
Cost for painting with black colour =Rs (528×0.05) = Rs26.40
Therefore, the total painting cost is:
= Rs(2757.86 +26.40)
= Rs 2784.26
3. The diameter of a sphere is decreased by 25%. By what percent does its curved surface area decrease?
Solution:
Let the diameter of the sphere be “d”.
Radius of sphere, r1 = d/2
New radius of sphere, say r2 = (d/2)×(1-25/100) = 3d/8
Curved surface area of sphere, (CSA)1 = 4πr12 = 4π×(d/2)2 = πd2 …(1)
Curved surface area of sphere when radius is decreased (CSA)2 = 4πr22 = 4π×(3d/8)2 = (9/16)πd2 …(2)
From equation (1) and (2), we have
Decrease in surface area of sphere = (CSA)1 – (CSA)2
= πd2 – (9/16)πd2
= (7/16)πd2
= (7d2/16d2)×100 = 700/16 = 43.75% .
Therefore, the percentage decrease in the surface area of the sphere is 43.75% .
