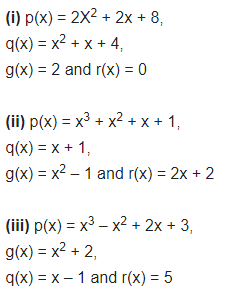NCERT Solutions Ch-2 Polynomials
Chapter 2 of Class 10th Maths, Polynomials, focuses on understanding the concept of polynomials, their degrees, and the various types of polynomials such as linear, quadratic, and cubic. This chapter also deals with the division algorithm for polynomials and explores the relationship between the zeroes and the coefficients of a polynomial. By solving the NCERT problems in this chapter, students will gain a solid foundation in handling polynomial expressions, finding their zeroes, and applying factorization techniques. The solutions provided aim to simplify complex problems and help students grasp the fundamental principles of polynomials, ensuring a clear understanding of the topic.
NCERT Solutions Maths Ch-2 Polynomials Exercise 2.1, 2.2, and 2.3
We try to teach you all Questions in easy way. We solve all chapter wise sums of maths textbook. In every chapter include NCERT solutions. For solutions of Exercise 2.1, 2.2, and 2.3 click on Tabs :
Question 1:
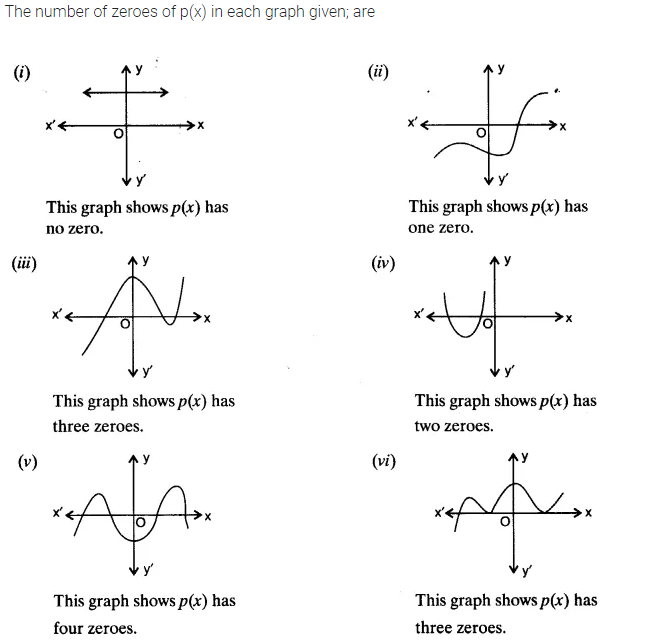
The graphs of y = p(x) are given below for some polynomials p(x). Find the number of zeroes of p(x) in each case.

Solution:
Question 1.
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and their coefficients:
(i) x2 – 2x – 8
x2 – 4x +2x – 8
x (x-4) 2 (x-4)
(x-4)(x+2)
x-4 = 0
x = 4
x+2 = 0
x = -2
So zeroes are 4 and -2
Verifications:
x2 – 4x +2x – 8
sum of zeroes = -b/a
4+(-2) = -(-2)/1
4-2 = 2/1
2 =2 verify
product of zeroes = c/a
4 x -2 = -8/1
-8 = -8 verify
(ii) 4s2 – 4s + 1
4s2 – 2s – 2s + 1
2s(2s-1) -1 (2s-1)
(2s-1)(2s-1)
2s-1 = 0
2s = 1
s = 1/2
so, zeroes are 1/2 , 1/2
Verifications:
4s2 – 4s + 1
sum of zeroes = -b/a
1/2 + 1/2 = -(-4)/4
2/2 = 4/4
1 =1 verify
product of zeroes = c/a
1/2 x 1/2 = 1/4
1/4 = 1/4 verify
(iii) 6x2 – 3 – 7x
first we write in order
6x2 – 7x – 3
6x2 – 9x + 2x -3
3x(2x – 3) +1(2x -3)
(2x – 3)(3x + 1)
2x – 3 = 0
2x = 3
x = 3/2
3x + 1 = 0
3x = -1
x = -1/3
so, zeroes are 3/2 and -1/3
Verifications:
6x2 – 7x – 3
sum of zeroes = -b/a
3/2 +(- 1/3) = -(-7)/6
3/2 – 1/3 = 7/6
7/6 = 7/6 verify
product of zeroes = c/a
3/2 x -1/3 = -3/6
-3/6 = -3/6 verify
(iv) 4u2 + 8u
4u is common so,
4u ( u + 2)
4u = 0
u = 0
u + 2 = 0
u = -2
Verifications:
4u2 + 8u
sum of zeroes = -b/a
0 + ( -2) = – 8/4
-2 = -2 verify
product of zeroes = c/a
0 x -2 = 0/4
0 = 0 verify
(v) t2 – 15
t2 – ( )2 . :
)2 . :  X
X  = 15
= 15
From Identitity A2 – B 2 = ( A + B ) (A – B)
(t +  ) (t –
) (t –  )
)
S0, zeroes are  and –
and – 
Verifications:
sum of zeroes = -b/a
 –
–  = 0 = – 0/1
= 0 = – 0/1
product of zeroes = c/a
 x –
x –  = – 15 = -15/1 verify
= – 15 = -15/1 verify
(vi) 3x2 – x – 4
3x2 + 3x – 4 x – 4
3x ( x+1) -4 (x+1)
(3x – 4) ( x + 1)
(3x – 4) = 0
x = 4/3
( x + 1) = 0
x = -1
S0, zeroes are 4/3 and -1
Verifications:
sum of zeroes = -b/a
4/3 + (-1) = -(-1)/3
4/3 – 1 = 1/3 = 1/3
product of zeroes = c/a
4/3 x -1 = -4/3 verify
Question 2.
Find a quadratic polynomial each with the given numbers as the sum and product of zeroes respectively:


Question 1.
Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
(i) p(x) = x3 – 3x2 + 5x – 3, g(x) = x2 – 2
(ii) p(x) = x4 – 3x2 + 4x + 5, g(x) = x2 + 1 – x
(iii) p(x) = x4– 5x + 6, g(x) = 2 – x2
Solution:

Question 2.
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial.
(i) t2 – 3, 2t4 + 3t3 – 2t2– 9t – 12
(ii) x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
(iii) x2 + 3x + 1, x5 – 4x3 + x2 + 3x + 1
Solution:

Question 3.
Obtain all other zeroes of 3x4 + 6x3 – 2x2 – 10x – 5, if two of its zeroes are


Question 5.
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and:
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solution: