Exercise 9.1
1. List five rational numbers between:
(i) -1 and 0
Solution:-
The five rational numbers between -1 and 0 are,
-1< (-2/3) < (-3/4) < (-4/5) < (-5/6) < (-6/7) < 0
(ii) -2 and -1
Solution:-
The five rational numbers between -2 and -1 are,
-2 < (-8/7) < (-9/8) < (-10/9) < (-11/10) < (-12/11) < -1
(iii) -4/5 and -2/3
Solution:-
The five rational numbers between -4/5 and -2/3 are,
-4/5 < (-13/12) < (-14/13) < (-15/14) < (-16/15) < (-17/16) < -2/3
(iv) -1/2 and 2/3
Solution:-
The five rational numbers between -1/2 and 2/3 are,
-1/2 < (-1/6) < (0) < (1/3) < (1/2) < (20/36) < 2/3
2. Write four more rational numbers in each of the following patterns:
(i) -3/5, -6/10, -9/15, -12/20, …..
Solution:-
In the above question, we can observe that the numerator and denominator are the multiples of 3 and 5.
= (-3 × 1)/ (5 × 1), (-3 × 2)/ (5 × 2), (-3 × 3)/ (5 × 3), (-3 × 4)/ (5 × 4)
Then, next four rational numbers in this pattern are,
= (-3 × 5)/ (5 × 5), (-3 × 6)/ (5 × 6), (-3 × 7)/ (5 × 7), (-3 × 8)/ (5 × 8)
= -15/25, -18/30, -21/35, -24/40 ….
(ii) -1/4, -2/8, -3/12, …..
Solution:-
In the above question, we can observe that the numerator and denominator are the multiples of 1 and 4.
= (-1 × 1)/ (4 × 1), (-1 × 2)/ (4 × 2), (-1 × 3)/ (1 × 3)
Then, next four rational numbers in this pattern are,
= (-1 × 4)/ (4 × 4), (-1 × 5)/ (4 × 5), (-1 × 6)/ (4 × 6), (-1 × 7)/ (4 × 7)
= -4/16, -5/20, -6/24, -7/28 ….
(iii) -1/6, 2/-12, 3/-18, 4/-24 …..
Solution:-
In the above question, we can observe that the numerator and denominator are the multiples of 1 and 6.
= (-1 × 1)/ (6 × 1), (1 × 2)/ (-6 × 2), (1 × 3)/ (-6 × 3), (1 × 4)/ (-6 × 4)
Then, next four rational numbers in this pattern are,
= (1 × 5)/ (-6 × 5), (1 × 6)/ (-6 × 6), (1 × 7)/ (-6 × 7), (1 × 8)/ (-6 × 8)
= 5/-30, 6/-36, 7/-42, 8/-48 ….
(iv) -2/3, 2/-3, 4/-6, 6/-9 …..
Solution:-
In the above question, we can observe that the numerator and denominator are the multiples of 2 and 3.
= (-2 × 1)/ (3 × 1), (2 × 1)/ (-3 × 1), (2 × 2)/ (-3 × 2), (2 × 3)/ (-3 × 3)
Then, next four rational numbers in this pattern are,
= (2 × 4)/ (-3 × 4), (2 × 5)/ (-3 × 5), (2 × 6)/ (-3 × 6), (2 × 7)/ (-3 × 7)
= 8/-12, 10/-15, 12/-18, 14/-21 ….
3. Give four rational numbers equivalent to:
(i) -2/7
Solution:-
The four rational numbers equivalent to -2/7 are,
= (-2 × 2)/ (7 × 2), (-2 × 3)/ (7 × 3), (-2 × 4)/ (7 × 4), (-2 × 5)/ (7× 5)
= -4/14, -6/21, -8/28, -10/35
(ii) 5/-3
Solution:-
The four rational numbers equivalent to 5/-3 are,
= (5 × 2)/ (-3 × 2), (5 × 3)/ (-3 × 3), (5 × 4)/ (-3 × 4), (5 × 5)/ (-3× 5)
= 10/-6, 15/-9, 20/-12, 25/-15
(iii) 4/9
Solution:-
The four rational numbers equivalent to 5/-3 are,
= (4 × 2)/ (9 × 2), (4 × 3)/ (9 × 3), (4 × 4)/ (9 × 4), (4 × 5)/ (9× 5)
= 8/18, 12/27, 16/36, 20/45
4. Draw the number line and represent the following rational numbers on it:

Solution:-
We know that 3/4 is greater than 0 and less than 1.
∴it lies between 0 and 1. It can be represented on number line as,

5. The points P, Q, R, S, T, U, A and B on the number line are such that, TR = RS = SU and AP = PQ = QB. Name the rational numbers represented by P, Q, R and S.
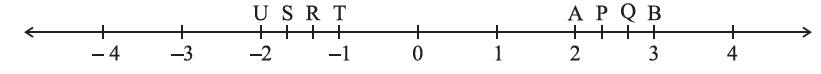
Solution:-
By observing the figure, we can say that,
The distance between A and B = 1 unit
And it is divided into 3 equal parts = AP = PQ = QB = 1/3
P = 2 + (1/3)
= (6 + 1)/ 3
= 7/3
Q = 2 + (2/3)
= (6 + 2)/ 3
= 8/3
Similarly,
The distance between U and T = 1 unit
And it is divided into 3 equal parts = TR = RS = SU = 1/3
R = – 1 – (1/3)
= (- 3 – 1)/ 3
= – 4/3
S = – 1 – (2/3)
= – 3 – 2)/ 3
= – 5/3
6. Which of the following pairs represent the same rational number?
(i) (-7/21) and (3/9)
Solution:-
We have to check the given pair represents the same rational number.
Then,
-7/21 = 3/9
-1/3 = 1/3
∵ -1/3 ≠ 1/3
∴ -7/21 ≠ 3/9
So, the given pair is not represents the same rational number.
(ii) (-16/20) and (20/-25)
Solution:-
We have to check the given pair represents the same rational number.
Then,
-16/20 = 20/-25
-4/5 = 4/-5
∵ -4/5 = -4/5
∴ -16/20 = 20/-25
So, the given pair is represents the same rational number.
(iii) (-2/-3) and (2/3)
Solution:-
We have to check the given pair represents the same rational number.
Then,
-2/-3 = 2/3
2/3= 2/3
∵ 2/3 = 2/3
∴ -2/-3 = 2/3
So, the given pair is represents the same rational number.
(iv) (-3/5) and (-12/20)
Solution:-
We have to check the given pair represents the same rational number.
Then,
-3/5 = – 12/20
-3/5 = -3/5
∵ -3/5 = -3/5
∴ -3/5= -12/20
So, the given pair is represents the same rational number.
(v) (8/-5) and (-24/15)
Solution:-
We have to check the given pair represents the same rational number.
Then,
8/-5 = -24/15
8/-5 = -8/5
∵ -8/5 = -8/5
∴ 8/-5 = -24/15
So, the given pair is represents the same rational number.
(vi) (1/3) and (-1/9)
Solution:-
We have to check the given pair represents the same rational number.
Then,
1/3 = -1/9
∵ 1/3 ≠ -1/9
∴ 1/3 ≠ -1/9
So, the given pair is not represents the same rational number.
(vii) (-5/-9) and (5/-9)
Solution:-
We have to check the given pair represents the same rational number.
Then,
-5/-9 = 5/-9
∵ 5/9 ≠ -5/9
∴ -5/-9 ≠ 5/-9
So, the given pair is not represents the same rational number.
7. Rewrite the following rational numbers in the simplest form:
(i) -8/6
Solution:-
The given rational numbers can be simplified further,
Then,
= -4/3 … [∵ Divide both numerator and denominator by 2]
(ii) 25/45
Solution:-
The given rational numbers can be simplified further,
Then,
= 5/9 … [∵ Divide both numerator and denominator by 5]
(iii) -44/72
Solution:-
The given rational numbers can be simplified further,
Then,
= -11/18 … [∵ Divide both numerator and denominator by 4]
(iv) -8/10
Solution:-
The given rational numbers can be simplified further,
Then,
= -4/5 … [∵ Divide both numerator and denominator by 2]
8. Fill in the boxes with the correct symbol out of >, <, and =.
(i) -5/7 [ ] 2/3
Solution:-
The LCM of the denominators 7 and 3 is 21
∴ (-5/7) = [(-5 × 3)/ (7 × 3)] = (-15/21)
And (2/3) = [(2 × 7)/ (3 × 7)] = (14/21)
Now,
-15 < 14
So, (-15/21) < (14/21)
Hence, -5/7 [<] 2/3
(ii) -4/5 [ ] -5/7
Solution:-
The LCM of the denominators 5 and 7 is 35
∴ (-4/5) = [(-4 × 7)/ (5 × 7)] = (-28/35)
And (-5/7) = [(-5 × 5)/ (7 × 5)] = (-25/35)
Now,
-28 < -25
So, (-28/35) < (- 25/35)
Hence, -4/5 [<] -5/7
(iii) -7/8 [ ] 14/-16
Solution:-
14/-16 can be simplified further,
Then,
7/-8 … [∵ Divide both numerator and denominator by 2]
So, (-7/8) = (-7/8)
Hence, -7/8 [=] 14/-16
(iv) -8/5 [ ] -7/4
Solution:-
The LCM of the denominators 5 and 4 is 20
∴ (-8/5) = [(-8 × 4)/ (5 × 4)] = (-32/20)
And (-7/4) = [(-7 × 5)/ (4 × 5)] = (-35/20)
Now,
-32 > – 35
So, (-32/20) > (- 35/20)
Hence, -8/5 [>] -7/4
(v) 1/-3 [ ] -1/4
Solution:-
The LCM of the denominators 3 and 4 is 12
∴ (-1/3) = [(-1 × 4)/ (3 × 4)] = (-4/12)
And (-1/4) = [(-1 × 3)/ (4 × 3)] = (-3/12)
Now,
-4 < – 3
So, (-4/12) < (- 3/12)
Hence, 1/-3 [<] -1/4
(vi) 5/-11 [ ] -5/11
Solution:-
Since, (-5/11) = (-5/11)
Hence, 5/-11 [=] -5/11
(vii) 0 [ ] -7/6
Solution:-
Since every negative rational number is less than 0.
We have:
= 0 [>] -7/6
9. Which is greater in each of the following:
(i) 2/3, 5/2
Solution:-
The LCM of the denominators 3 and 2 is 6
(2/3) = [(2 × 2)/ (3 × 2)] = (4/6)
And (5/2) = [(5 × 3)/ (2 × 3)] = (15/6)
Now,
4 < 15
So, (4/6) < (15/6)
∴ 2/3 < 5/2
Hence, 5/2 is greater.
(ii) -5/6, -4/3
Solution:-
The LCM of the denominators 6 and 3 is 6
∴ (-5/6) = [(-5 × 1)/ (6 × 1)] = (-5/6)
And (-4/3) = [(-4 × 2)/ (3 × 2)] = (-12/6)
Now,
-5 > -12
So, (-5/6) > (- 12/6)
∴ -5/6 > -12/6
Hence, – 5/6 is greater.
(iii) -3/4, 2/-3
Solution:-
The LCM of the denominators 4 and 3 is 12
∴ (-3/4) = [(-3 × 3)/ (4 × 3)] = (-9/12)
And (-2/3) = [(-2 × 4)/ (3 × 4)] = (-8/12)
Now,
-9 < -8
So, (-9/12) < (- 8/12)
∴ -3/4 < 2/-3
Hence, 2/-3 is greater.
(iv) -¼, ¼
Solution:-
The given fraction is like friction,
So, -¼ < ¼
Hence ¼ is greater,
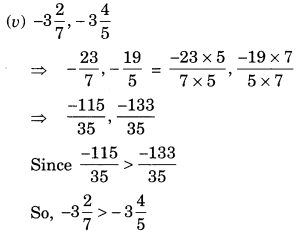
10. Write the following rational numbers in ascending order:
(i) -3/5, -2/5, -1/5
Solution:-
The given rational numbers are in form of like fraction,
Hence,
(-3/5)< (-2/5) < (-1/5)
(ii) -1/3, -2/9, -4/3
Solution:-
To convert the given rational numbers into like fraction we have to find LCM,
LCM of 3, 9, and 3 is 9
Now,
(-1/3)= [(-1 × 3)/ (3 × 9)] = (-3/9)
(-2/9)= [(-2 × 1)/ (9 × 1)] = (-2/9)
(-4/3)= [(-4 × 3)/ (3 × 3)] = (-12/9)
Clearly,
(-12/9) < (-3/9) < (-2/9)
Hence,
(-4/3) < (-1/3) < (-2/9)
(iii) -3/7, -3/2, -3/4
Solution:-
To convert the given rational numbers into like fraction we have to find LCM,
LCM of 7, 2, and 4 is 28
Now,
(-3/7)= [(-3 × 4)/ (7 × 4)] = (-12/28)
(-3/2)= [(-3 × 14)/ (2 × 14)] = (-42/28)
(-3/4)= [(-3 × 7)/ (4 × 7)] = (-21/28)
Clearly,
(-42/28) < (-21/28) < (-12/28)
Hence,
(-3/2) < (-3/4) < (-3/7)
Exercise 9.2
1. Find the sum:
(i) (5/4) + (-11/4)
Solution:-
We have:
= (5/4) – (11/4)
= [(5 – 11)/4] … [∵ denominator is same in both the rational numbers]
= (-6/4)
= -3/2 … [∵ Divide both numerator and denominator by 3]
(ii) (5/3) + (3/5)
Solution:-
Take the LCM of the denominators of the given rational numbers.
LCM of 3 and 5 is 15
Express each of the given rational numbers with the above LCM as the common denominator.
Now,
(5/3)= [(5×5)/ (3×5)] = (25/15)
(3/5)= [(3×3)/ (5×3)] = (9/15)
Then,
= (25/15) + (9/15) … [∵ denominator is same in both the rational numbers]
= (25 + 9)/15
= 34/15
(iii) (-9/10) + (22/15)
Solution:-
Take the LCM of the denominators of the given rational numbers.
LCM of 10 and 15 is 30
Express each of the given rational numbers with the above LCM as the common denominator.
Now,
(-9/10)= [(-9×3)/ (10×3)] = (-27/30)
(22/15)= [(22×2)/ (15×2)] = (44/30)
Then,
= (-27/30) + (44/30) … [∵ denominator is same in both the rational numbers]
= (-27 + 44)/30
= (17/30)
(iv) (-3/-11) + (5/9)
Solution:-
We have,
= 3/11 + 5/9
Take the LCM of the denominators of the given rational numbers.
LCM of 11 and 9 is 99
Express each of the given rational numbers with the above LCM as the common denominator.
Now,
(3/11)= [(3×9)/ (11×9)] = (27/99)
(5/9)= [(5×11)/ (9×11)] = (55/99)
Then,
= (27/99) + (55/99) … [∵ denominator is same in both the rational numbers]
= (27 + 55)/99
= (82/99)
(v) (-8/19) + (-2/57)
Solution:-
We have
= -8/19 – 2/57
Take the LCM of the denominators of the given rational numbers.
LCM of 19 and 57 is 57
Express each of the given rational numbers with the above LCM as the common denominator.
Now,
(-8/19)= [(-8×3)/ (19×3)] = (-24/57)
(-2/57)= [(-2×1)/ (57×1)] = (-2/57)
Then,
= (-24/57) – (2/57) … [∵ denominator is same in both the rational numbers]
= (-24 – 2)/57
= (-26/57)

2. Find
(i) 7/24 – 17/36
Solution:-
Take the LCM of the denominators of the given rational numbers.
LCM of 24 and 36 is 72
Express each of the given rational numbers with the above LCM as the common denominator.
Now,
(7/24)= [(7×3)/ (24×3)] = (21/72)
(17/36)= [(17×2)/ (36×2)] = (34/72)
Then,
= (21/72) – (34/72) … [∵ denominator is same in both the rational numbers]
= (21 – 34)/72
= (-13/72)
(ii) 5/63 – (-6/21)
Solution:-
We can also write -6/21 = -2/7
= 5/63 – (-2/7)
We have,
= 5/63 + 2/7
Take the LCM of the denominators of the given rational numbers.
LCM of 63 and 7 is 63
Express each of the given rational numbers with the above LCM as the common denominator.
Now,
(5/63)= [(5×1)/ (63×1)] = (5/63)
(2/7)= [(2×9)/ (7×9)] = (18/63)
Then,
= (5/63) + (18/63) … [∵ denominator is same in both the rational numbers]
= (5 + 18)/63
= 23/63
(iii) -6/13 – (-7/15)
Solution:-
We have,
= -6/13 + 7/15
LCM of 13 and 15 is 195
Express each of the given rational numbers with the above LCM as the common denominator.
Now,
(-6/13)= [(-6×15)/ (13×15)] = (-90/195)
(7/15)= [(7×13)/ (15×13)] = (91/195)
Then,
= (-90/195) + (91/195) … [∵ denominator is same in both the rational numbers]
= (-90 + 91)/195
= (1/195)
(iv) -3/8 – 7/11
Solution:-
Take the LCM of the denominators of the given rational numbers.
LCM of 8 and 11 is 88
Express each of the given rational numbers with the above LCM as the common denominator.
Now,
(-3/8)= [(-3×11)/ (8×11)] = (-33/88)
(7/11)= [(7×8)/ (11×8)] = (56/88)
Then,
= (-33/88) – (56/88) … [∵ denominator is same in both the rational numbers]
= (-33 – 56)/88
= (-89/88)
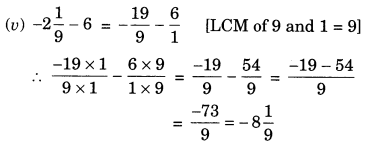
3. Find the product:
(i) (9/2) × (-7/4)
Solution:-
The product of two rational numbers = (product of their numerator)/ (product of their denominator)
The above question can be written as (9/2) × (-7/4)
We have,
= (9×-7)/ (2×4)
= -63/8
(ii) (3/10) × (-9)
Solution:-
The product of two rational numbers = (product of their numerator)/ (product of their denominator)
The above question can be written as (3/10) × (-9/1)
We have,
= (3×-9)/ (10×1)
= -27/10
(iii) (-6/5) × (9/11)
Solution:-
The product of two rational numbers = (product of their numerator)/ (product of their denominator)
We have,
= (-6×9)/ (5×11)
= -54/55
(iv) (3/7) × (-2/5)
Solution:-
The product of two rational numbers = (product of their numerator)/ (product of their denominator)
We have,
= (3×-2)/ (7×5)
= -6/35
(v) (3/11) × (2/5)
Solution:-
The product of two rational numbers = (product of their numerator)/ (product of their denominator)
We have,
= (3×2)/ (11×5)
= 6/55
(vi) (3/-5) × (-5/3)
Solution:-
The product of two rational numbers = (product of their numerator)/ (product of their denominator)
We have,
= (3×-5)/ (-5×3)
On simplifying,
= (1×-1)/ (-1×1)
= -1/-1
= 1
4. Find the value of:
(i) (-4) ÷ (2/3)
Solution:-
We have,
= (-4/1) × (3/2) … [∵ reciprocal of (2/3) is (3/2)]
The product of two rational numbers = (product of their numerator)/ (product of their denominator)
= (-4×3) / (1×2)
= (-2×3) / (1×1)
= -6
(ii) (-3/5) ÷ 2
Solution:-
We have,
= (-3/5) × (1/2) … [∵ reciprocal of (2/1) is (1/2)]
The product of two rational numbers = (product of their numerator)/ (product of their denominator)
= (-3×1) / (5×2)
= -3/10
(iii) (-4/5) ÷ (-3)
Solution:-
We have,
= (-4/5) × (1/-3) … [∵ reciprocal of (-3) is (1/-3)]
The product of two rational numbers = (product of their numerator)/ (product of their denominator)
= (-4× (1)) / (5× (-3))
= -4/-15
= 4/15
(iv) (-1/8) ÷ 3/4
Solution:-
We have,
= (-1/8) × (4/3) … [∵ reciprocal of (3/4) is (4/3)]
The product of two rational numbers = (product of their numerator)/ (product of their denominator)
= (-1×4) / (8×3)
= (-1×1) / (2×3)
= -1/6
(v) (-2/13) ÷ 1/7
Solution:-
We have,
= (-2/13) × (7/1) … [∵ reciprocal of (1/7) is (7/1)]
The product of two rational numbers = (product of their numerator)/ (product of their denominator)
= (-2×7) / (13×1)
= -14/13
(vi) (-7/12) ÷ (-2/13)
Solution:-
We have,
= (-7/12) × (13/-2) … [∵ reciprocal of (-2/13) is (13/-2)]
The product of two rational numbers = (product of their numerator)/ (product of their denominator)
= (-7× 13) / (12× (-2))
= -91/-24
= 91/24
(vii) (3/13) ÷ (-4/65)
Solution:-
We have,
= (3/13) × (65/-4) … [∵ reciprocal of (-4/65) is (65/-4)]
The product of two rational numbers = (product of their numerator)/ (product of their denominator)
= (3×65) / (13× (-4))
= 195/-52
= -15/4


