Exercise 11.1
In each of the following, give the justification of the construction also:
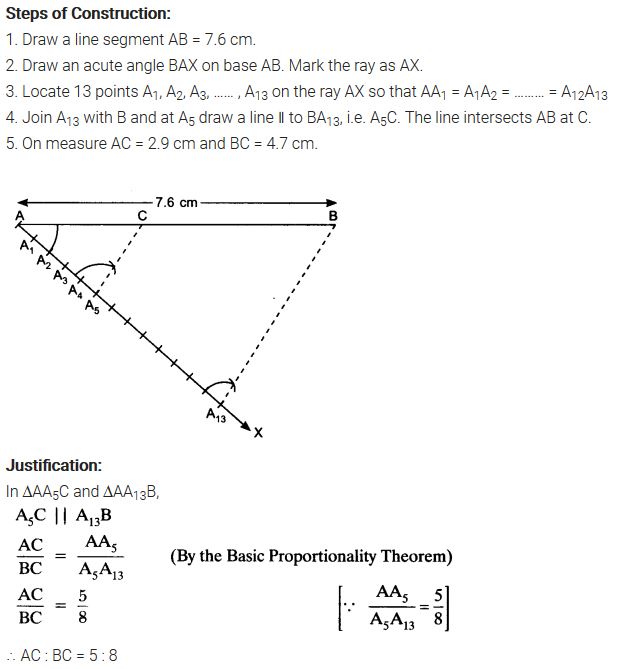
1. Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts.
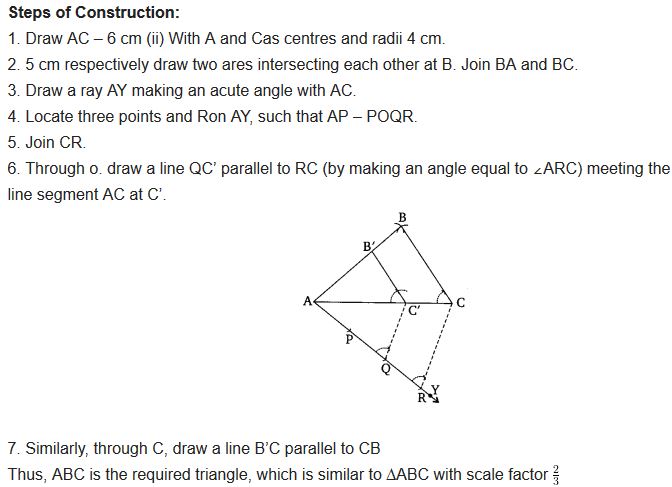
2. Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are 2/3 of
the corresponding sides of the first triangle.

3. Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are 7/5 of the corresponding sides of the first triangle
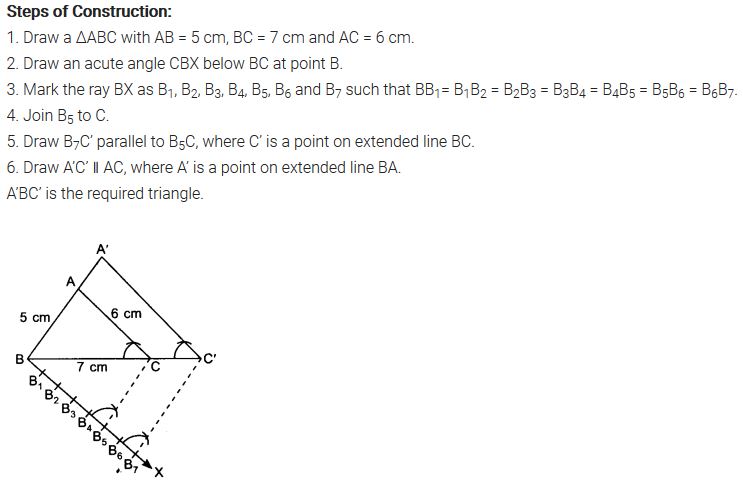



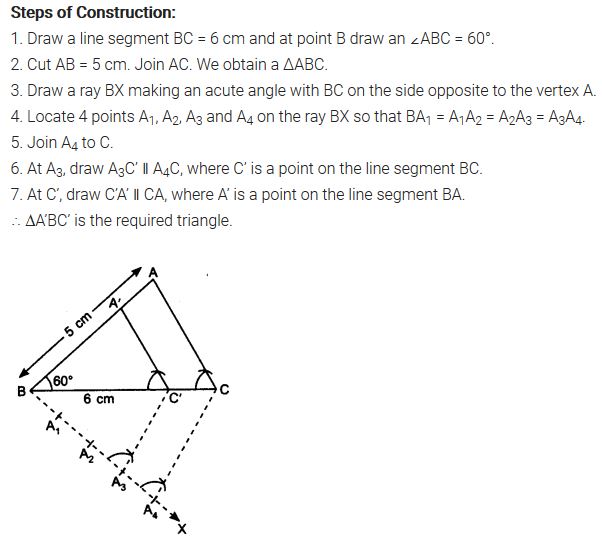
5. Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are 3/4 of the corresponding sides of the triangle ABC.

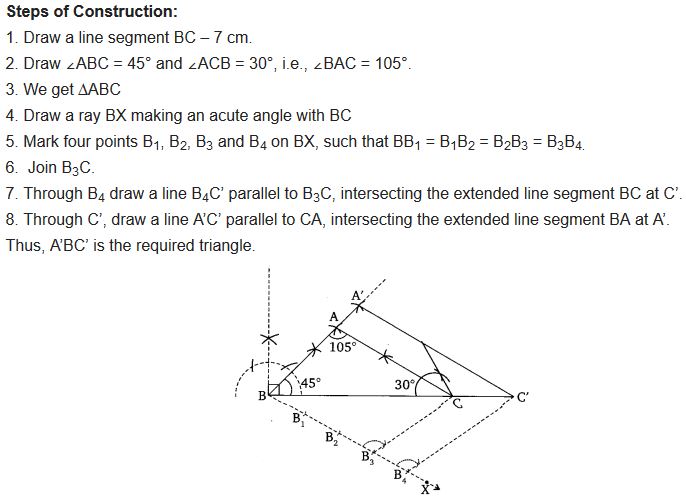
6. Draw a triangle ABC with side BC = 7 cm, ∠ B = 45°, ∠ A = 105°. Then, construct a triangle whose sides are 4/3 times the corresponding sides of ∆ ABC.

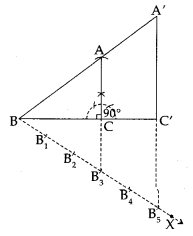
7. Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are 5/3 times the corresponding sides of the given triangle.
Solution:
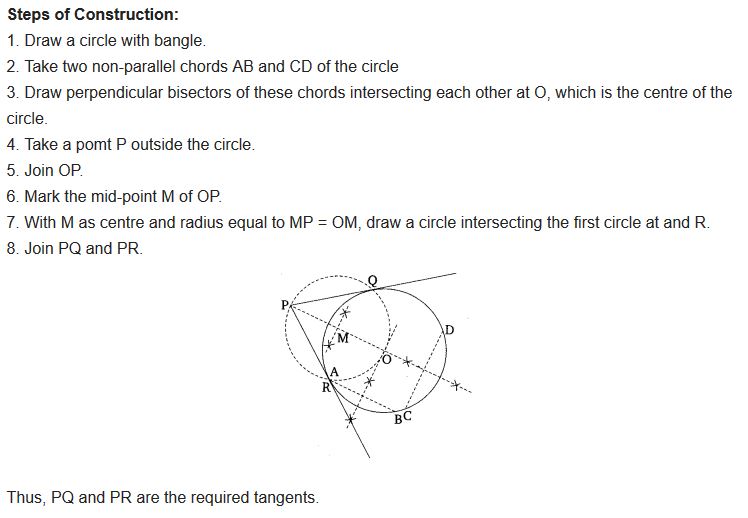
Steps of Construction:
1. Construct a ∆ABC, such that BC = 4 cm, CA = 3 cm and ∠BCA = 90°
2. Draw a ray BX making an acute angle with BC.
3. Mark five points B1, B2, B3, B4 and B5 on BX, such that BB1 = B1B2 = B2B3 = B3B4 = B4B5.
4. Join B3C.
5. Through B5, draw B5C’ parallel to B3C intersecting BC produced at C’.
6. Through C’, draw C’A’ parallel to CA intersecting AB produced at A’.
Thus, ∆A’BC’ is the required right triangle.

Exercise 11.2
Question 1.
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Solution:

Question 2.
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Solution:

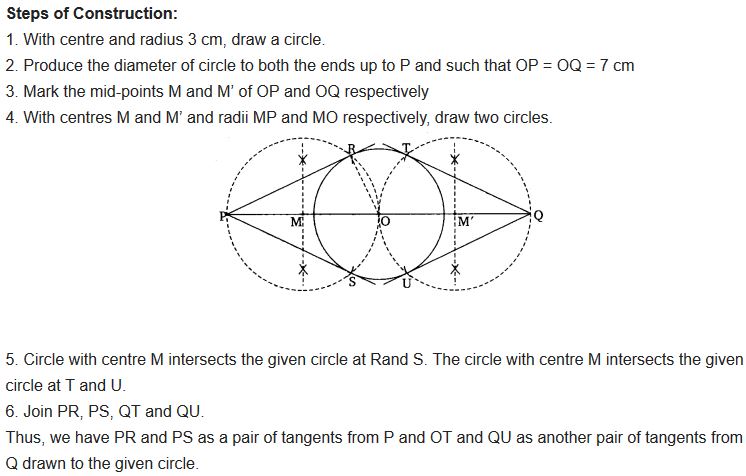
Question 3.
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Solution:

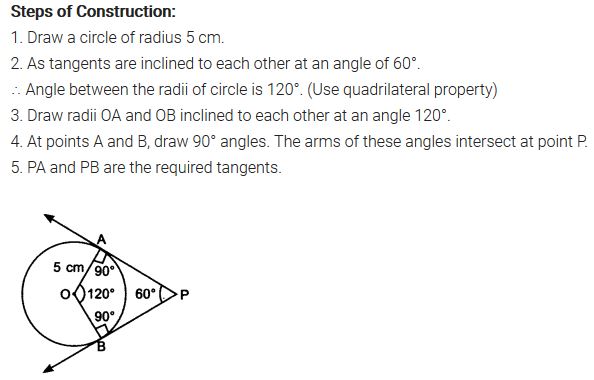
Question 4.
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
Solution:

Question 5.
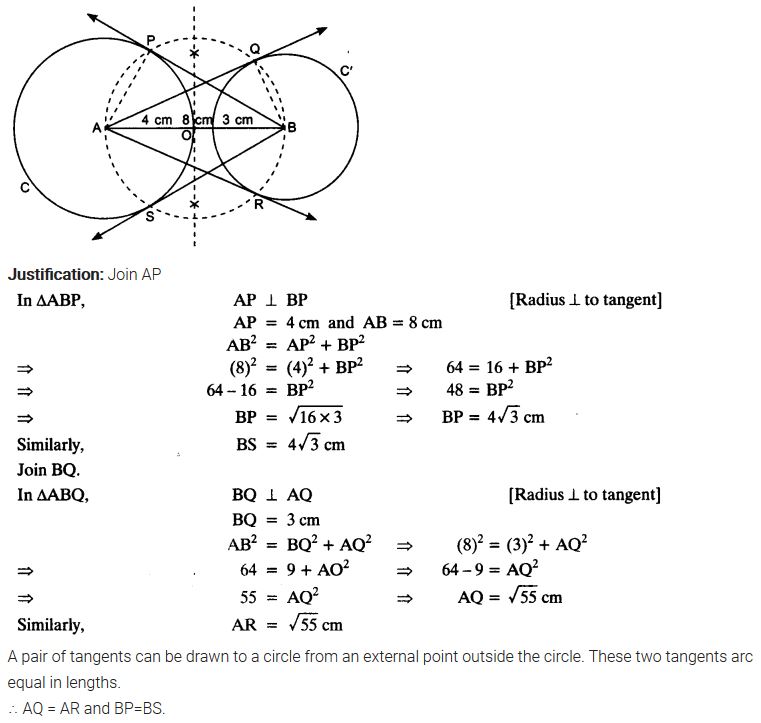
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Solution: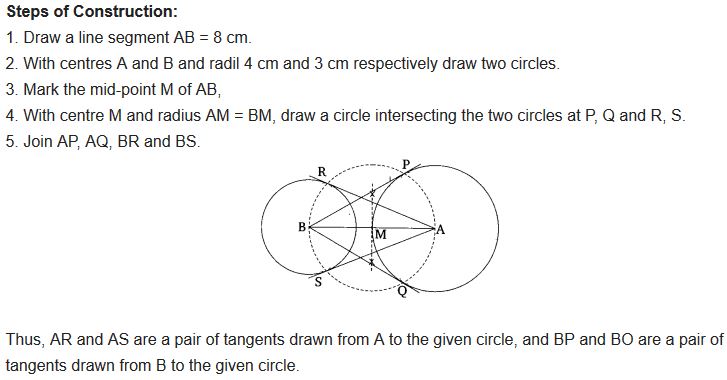
Question 6.
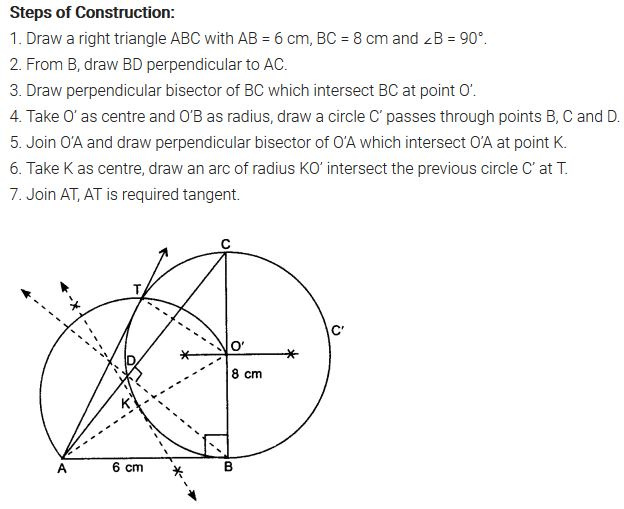
Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠B = 90°. BD is the perpendicular Burn B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Solution:

Question 7.
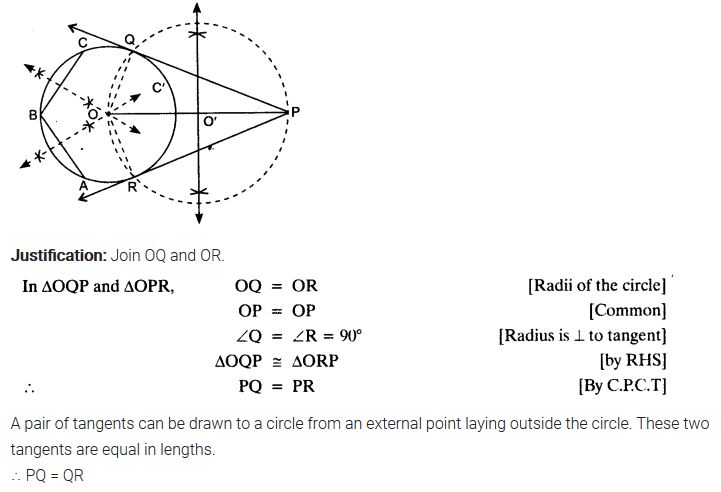
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.
Solution: