Exercise 10.1
Question 1.
Draw a line, say AB, take a point C outside it. Through C draw a line parallel to AB using ruler and compasses only.
Solution:
Steps of construction:
(i) Draw a line AB.
(ii) Take any point D on it.
(iii) Join the given point C to D and mark ∠1 to ∠CDB.
(iv) Mark ∠1 = ∠2 at C and produce to both side.
(v) MN is the required line.
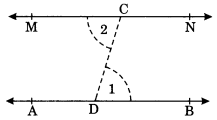
Using the Property of Alternate Angles
Question 2.
Draw a line Z. Draw a perpendicular to l at any point on l. On this perpendicular choose a point X, 4 cm away from l. Through X, draw a line m parallel to l.
Solution: ‘Steps of construction:
(i) Draw a given line Z and take any point P on it.
(ii) Draw a perpendicular line at P to the line Z such that PX = 4 cm.
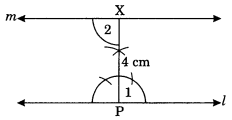
(iii) Draw ∠2 = ∠1 i.e. 90° at PX and produce the line both sides.
(iv) m is the required line parallel to Z through X.
Using Properties of Alternate Angles
Question 3.
Let l be a line and P be a point not on l. Through P, draw a line m parallel to P. Now join P to any point Q on l. Choose any other point R on m. Through R, draw a line parallel to PQ. Let this meet l at S. What shape do the two sets of parallel lines enclose?
Solution:
Steps of Construction:
(i) Draw a line l and take any point P not on l.
(ii) Draw a line m parallel to l through P.
(iii) Join P and Q.
(iv) PQ makes ∠1 with l and ∠2 with m which are equal angles.
(v) Take any point R on m and draw ∠3 equal to ∠ 2 to meet l at S such that PQ || RS.
(vi) Since l || m and PQ || RS. Therefore, PQSR is a parallelogram.
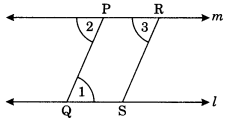
Using the properties of parallel lines and transversal line and alternate angles
Exercise 10.2
Question 1.
Construct ∆XYZ in which XY = 4.5 cm, YZ = 5 cm and ZX = 6 cm.
Solution:
Steps of construction:
(i) Draw XY = 4.5 cm.
(ii) Draw an arc with centre Y and radius 5 cm.
(iii) Draw another arc with centre X and radius 6 cm to meet the first arc at Z.
(iv) Join ZY and ZX.
(v) XYZ is the required triangle.
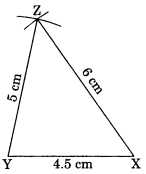
Using SSS criterion
Question 2.
Construct an equilateral triangle of side 5.5 cm. Solution: Steps of construction:
(i) Draw BC = 5.5 cm.
(ii) Draw two arcs with centres B and C and same radius of 5.5 cm to meet each other at A.
(iii) Join AB and AC.
(iv) ABC is the required triangle.
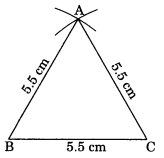
Using SSS criterion
Question 3.
Draw ∆PQR with PQ = 4 cm, QR = 3.5 cm and PR = 4 cm. What type of triangle is this?
Solution:
Steps of construction:
(i) Draw QR = 3.5 cm.
(ii) Draw two arcs with centre Q and R and same radius of 4 cm to meet each other at P.
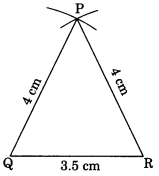
(iii) Join PQ and PR.
(iv) PQR is the required triangle.
(v) Since PQ = PR = 4 cm, therefore APQR is an isosceles triangle.
Using SSS Criterion
Question 4.
Construct ∆ABC such that AB = 2.5 cm, BC = 6 cm and AC = 6.5 cm. Measure ∠B.
Solution:
Steps of construction:
(i) Draw BC = 6 cm.
(ii) Draw two arcs with centres B and C and radius 2.5 cm and 6.5 cm respectively to meet each other at A.
(iii) Join AB and AC.
(iv) ABC is the required triangle.
[Using SSS criterion]

Exercise 10.3
Question 1.
Construct ∆DEF such that DE = 5 cm, DF = 3 cm and m ∠DEF = 90°.

Solution:
Steps of construction:
(i) Draw DF = 3 cm.
(ii) Draw an angle of 90° at D and cut DE = 5 cm.
(iii) Join EF.
(iv) EPF is the required triangle.
Using SAS property
Question 2.
Construct an isosceles triangle in which the lengths of each of its equal sides is 6.5 cm and the angle between them is 110°.
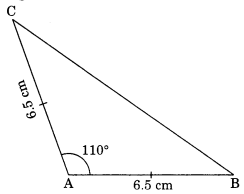
Solution:
Steps of construction:
(i) Draw AB = 6.5 cm.
(ii) Draw angle of 110° at A and cut AC = 6.5 cm.
(iii) Join C to B.
(iv) CAB is the required triangle.
[Using SAS criterion]
Question 3.
Construct ∆ABC with BC = 7.5 cm, AC = 5 cm and m ∠C = 60°.

Solution:
Steps of construction:
(i) Draw BC = 7.5 cm.
(ii) Draw ∠C = 60° such that AC = 5 cm.
(iii) Join A to B.
(iv) ABC is the required triangle.
[Using SAS Criterion]
Exercise 10.4
Question 1.
Construct ∆ABC, given m ∠A = 60°, m ∠B = 30° and AB = 5.8 cm.
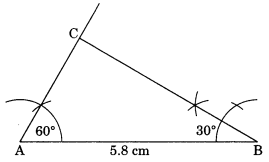
Solution:
Steps of construction:
(i) Draw AB = 5.8 cm.
(ii) Draw ∠A = 60° and ∠B = 30° to meet each other at C.
(iii) ABC is the required triangle.
Using ASA criterion
Question 2.
Construct ∆PQR if PQ = 5 cm, m ∠PQR = 105° and m∠QRP = 40°.
(Hint: Recall angle-sum property of a triangle)
Solution:
Given: m∠PQR = 40°, m∠QRP = 105°
∵ m∠PQR + m∠QRP + ∠QPR = 180° (Angle sum property of a triangle)
105° + 40° + ∠QPR = 180°
145° + ∠QPR = 180°
∴ ∠QPR = 180° – 145° = 35°
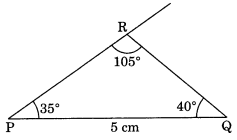
Steps of construction:
(i) Draw PQ = 5 cm.
(ii) Draw ∠QPR = 35° and ∠PQR = 40° to meet each other at R.
(iii) ∆PQR is the required triangle.
[Using AAS or ASA criterion]
Question 3.
Examine whether you can construct ∆DEF such that EF = 7.2 cm, m∠E = 110° and m∠F = 80°. Justify your answer.
Solution:
To construct ∆DEF with the given measurement, is not possible.
∵ m∠E + m∠F = 110° + 80°
= 190° > 180° [Sum of the angles of a triangle = 180°]
∴ ADEF is not possible to construct.
Exercise 10.5
Question 1.
Construct the right angled ∆PQR, where m∠Q = 90°, QR = 8 cm and PR = 10 cm.
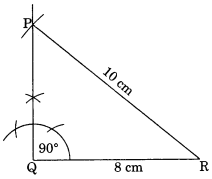
Solution:
Steps of construction:
(i) Draw QR = 8 cm.
(ii) Draw m∠Q = 90°.
(iii) Draw an arc with centre R and radius 10 cm to cut the perpendicular line at P.
(iv) ∆PQR is the required triangle.
[Using RHS criterion]
Question 2.
Construct a right-angled triangle whose hypotenuse is 6 cm long and one of the legs is 4 cm long.

Solution:
Steps of construction:
(i) Draw AB = 4 cm.
(ii) Draw ∠A = 90°.
(iii) Cut BC = 6 cm.
(iv) ∆CAB is the required right-angled triangle.
[Using RHS criterion]
Question 3.
Construct an isosceles right-angled triangle ABC, where m∠ACB = 90° and AC = 6 cm.

Solution:
Steps of construction:
(i) Draw AC = 6 cm.
(ii) Draw ∠A =∠C = 45° to meet each other at B such that m∠B = 90°.
(iii) ∆ABC is right-angled isosceles triangle which is the required triangle.
[Using RHS criterion]


