Exercise 11.1
Question 1.
A square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?
Solution:
Perimeter of figure (a) = 4 × side = 4 × 60 = 240 m
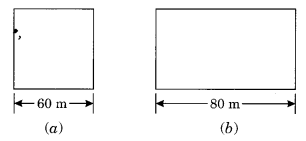
Perimeter of figure (b) = 2 [l + b]
Perimeter of figure (b) = Perimeter of figure (a)
2[l + b] = 240
⇒ 2 [80 + b] = 240
⇒ 80 + b = 120
⇒ b = 120 – 80 = 40 m
Area of figure (a) = (side)2 = 60 × 60 = 3600 m2
Area of figure (b) = l × b = 80 × 40 = 3200 m2
So, area of figure (a) is longer than the area of figure (b).
Question 2.
Mrs Kaushik has a square plot with the measurement as shown in the figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a garden around the house at the rate of ₹ 55 per m2.
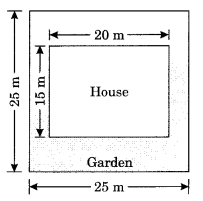
Solution:
Area of the plot = side × side = 25 m × 25 m = 625 m2
Area of the house = l × b = 20 m × 15 m = 300 m2
Area of the garden to be developed = Area of the plot – Area of the house = 625 m2 – 300 m2 = 325 m2
Cost of developing the garden = ₹ 325 × 55 = ₹ 17875
Question 3.
The shape of a garden is rectangular in the middle and semicircular at the ends as shown in the diagram. Find the area and the perimeter of this garden. [Length of rectangle is 20 – (3.5 + 3.5) metres]
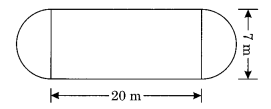
Solution:
Length of the rectangle = 20 – (3.5 + 3.5) = 20 – 7 = 13 m
Area of the rectangle = l × b = 13 × 7 = 91 m2
Area of two circular ends = 2(1/2 πr2)
= πr2
= 22/7 × 7/2 × 7/2
= 77/2 m2
= 38.5 m2
Total area = Area of the rectangle + Area of two ends = 91 m2 + 38.5 m2 = 129.5 m2
Total perimeter = Perimeter of the rectangle + Perimeter of two ends
= 2 (l + b) + 2 × (πr) – 2(2r)
= 2 (13 + 7) + 2(22/7 × 72) – 4 × 7/2
= 2 × 20 + 22 – 14
= 40 + 22 – 14
= 48 m
Question 4.
A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m2? (If required you can split the tiles in whatever way you want to fill up the corners).
Solution:
Area of the floor = 1080 m2 = 1080 × 10000 cm2 = 10800000 cm2 [∵ 1 m2 = 10000 cm2]
Area of 1 tile = 1 × base × height = 1 × 24 × 10 = 240 cm2
Number of tiles required

= 45000 tiles
Question 5.
An ant is moving around a few food pieces of different shapes scattered on the floor. For which food-piece would the ant have to take a longer round? Remember, the circumference of a circle can be obtained by using the expression C = 2πr, where r is the radius of the circle.
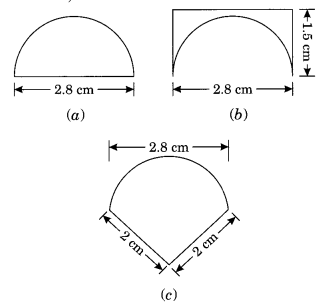
Solution:

Exercise 11.2
Question 1.
The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.
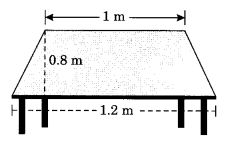
Solution:
Area of the trapezium = 12 × (a + b) × h
= 1/2 × (1.2 + 1) × 0.8
= 1/2 × 2.2 × 0.8
= 0.88 m2
Hence, the required area = 0.88 m2
Question 2.
The area of a trapezium is 34 cm2 and the length of one of the parallel sides is 10 cm and its height is 4 cm. Find the length of the other parallel sides.
Solution:
Given: Area of trapezium = 34 cm2
Length of one of the parallel sides a = 10 cm
height h = 4 cm
Area of the trapezium = 1/2 × (a + b) × h
34 = 1/2 × (10 + b) × 4
⇒ 34 = (10 + b) × 2
⇒ 17 = 10 + b
⇒ b = 17 – 10 = 7 cm
Hence, the required length = 7 cm.
Question 3.
Length of the fence of a trapezium-shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.
Solution:
Given:
AB + BC + CD + DA = 120 m .
BC = 48 m, CD = 17 m, AD = 40 m
AB = 120 m – (48 m + 17 m + 40 m) = 120 – 105 m = 15 m
Area of the trapezium ABCD = 12 × (BC + AD) × AB
= 12 × (48 + 40) × 15
= 12 × 88 × 15
= 44 × 15 = 660 m2.
Hence, the required area = 660 m2
Question 4.
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.
Solution:
Area of the field = area of ∆ABD + area of ∆BCD

= 1/2 × b × h + 1/2 × b × h
= 1/2 × 24 × 13 + 1/2 × 24 × 8
= 12 × 13 + 12 × 8
= 12 × (13 + 8)
= 12 × 21
= 252 m2
Hence, the required area of the field = 252 m2.
Question 5.
The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Solution:
Here, d1 = 7.5 cm, d2 = 12 cm
Area of the rhombus = 1/2 × d1 × d2
= 1/2 × 7.5 × 12
= 7.5 × 6
= 45 cm2
Hence, area of the rhombus = 45 cm2.
Question 6.
Find the area of a rhombus whose side is 5 cm and whose altitude is 4.8 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
Solution:
Given: Side = 5 cm
Altitude = 4.8 cm
Length of one diagonal = 8 cm
Area of the rhombus = Side × Altitude = 5 × 4.8 = 24 cm2
Area of the rhombus = 1/2 × d1 × d2
24 = 1/2 × d1 × d2
24 = 4d2
d2 = 6 cm
Hence, the length of other diagonal = 6 cm.
Question 7.
The floor of a building consists of 3000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per m2 is ₹ 4.
Solution:
Given: Number of tiles = 3000
Length of the two diagonals of a tile = 45 cm and 30 cm
Area of one tile = 1/2 × d1 × d2
= 1/2 × 45 × 30
= 45 × 15
= 675 cm2
Area covered by 3000 tiles = 3000 × 675 cm2 = 2025000 cm2 = 202.5 m2
Cost of polishing the floor = 202.5 × 4 = ₹ 810
Hence, the required cost = ₹ 810.
Question 8.
Mohan wants to buy a trapezium-shaped field. Its side along the river is parallel to and twice the side along the road. If the area of this field is 10500 m2 and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.
Solution:
Let the side of the trapezium (roadside) be x cm.
The opposite parallel side = 2x m
h = 100 m
Area = 10500 m2
Area of trapezium = 1/2 (a + b) × h
10500 = 1/2 (2x + x) × 100
2 × 10500 = 3x × 100
21000 = 300x
x = 70 m
So, AB = 2x = 2 × 70 = 140 m
Hence, the required length = 140 m.
Question 9.
The top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.
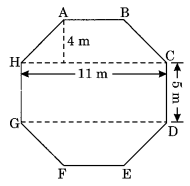
Solution:
Area of the octagonal surface = area of trapezium ABCH + area of rectangle HCDG + area of trapezium GDEF
Area of trapezium ABCH = Area of trapezium GDEF
= 1/2 (a + b) × h
= 1/2 (11 + 5) × 4
= 1/2 × 16 × 4
= 32 m2
Area of rectangle HCDG = l × b = 11 m × 5 m = 55 m2
Area of the octagonal surface = 32 m2 + 55 m2 + 32 m2 = 119 m2
Hence, the required area = 119 m2.
Question 10.
There is a pentagonal shaped park as shown in the figure. For finding its area Jyoti and Kavita divided it in two different ways.
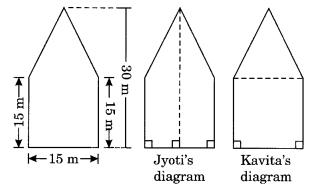
Find the area of this park using both ways. Can you suggest some other way of finding its area?
Solution:
(i) From Jyoti’s diagram:
Area of the pentagonal shape = Area of trapezium ABCD + Area of trapezium ADEF
= 2 × Area of trapezium ABCD
= 2 × 12 (a + b) × h
= (15 + 30) × 7.5
= 45 × 7.5
= 337.5 m2
(ii) From Kavita’s diagram:
Area of the pentagonal shape = Area of ∆ABE + Area of square BCDE
= 1/2 × b × h + 15 × 15
= 1/2 × 15 × 15 + 225
= 112.5 + 225
= 337.5 m
Exercise 11.3
Question 1.
There are two cuboidal boxes as shown in the figure. Which box requires the lesser amount of material to make?

Solution:
(a) Volume of the cuboid = l × b × h = 60 × 40 × 50 = 120000 cm3
(b) Volume of cube = (Side)3 = (50)3 = 50 × 50 × 50 = 125000 cm3
Cuboidal box (a) requires lesser amount of material.
Question 2.
A suitcase with measures 80 cm × 48 cm × 24 cm is to be covered with a tarpaulin cloth. How many metres of tarpaulin of width 96 cm is required to cover 100 such suitcases?
Solution:
Measurement of the suitcase = 80 cm × 48 cm × 24 cm
l = 80 cm, b = 48 cm and h = 24 cm
Total surface area of the suitcase = 2[lb + bh + hl]
= 2 [80 × 48 + 48 × 24 + 24 × 80]
= 2 [3840 + 1152 + 1920]
= 2 × 6912
= 13824 cm2
Area of tarpaulin = length × breadth = l × 96 = 96l cm2
Area of tarpaulin = Area of 100 suitcase
96l = 100 × 13824
l = 100 × 144 = 14400 cm = 144 m
Hence, the required length of the cloth = 144 m.
Question 3.
Find the side of a cube whose surface area is 600 cm2?
Solution:
Total surface area of a cube = 6l2
6l2 = 600
l2 = 100
l = √100 = 10 cm
Hence, the required length of side = 10 cm.
Question 4.
Rukhsar painted the outside of the cabinet of measure 1 m × 2 m × 1.5 m. How much surface area did she cover if she painted all except the bottom of the cabinet?
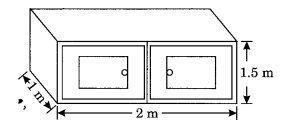
Solution:
l = 2 m, b = 1.5 m, h = 1 m
Area of the surface to be painted = Total surface area of box – Area of base of box
= 2 [lb + bh + hl] – lb
= 2[2 × 1.5 + 1.5 × 1 + 1 × 2] – 2 × 1
= 2[3 + 1.5 + 2] – 2
= 2[6.5] – 2
= 13 – 2
= 11 m2
Hence, the required area = 11 m2.
Question 5.
Daniel is painting the walls and ceiling of a cuboidal hall with length, breadth and height of 15 m, 10 m and 7 m respectively. From each can of paint 100 m2 of the area is painted. How many cans of paint will she need to paint the room?
Solution:
Surface area of a cuboidal hall without bottom = Total surface area – Area of base
= 2 [lb + bh + hl] – lb
= 2 [15 × 10 + 10 × 7 + 7 × 15] – 15 × 10
= 2[150 + 70 + 105] – 150
= 2 [325] – 150
= 650 – 150
= 500 m2
Area of the paint in one can = 100 m2
Number of cans required = 500/100 = 5 cans.
Question 6.
Describe how the two figures at the right are alike and how they are different. Which box has a larger lateral surface area?

Solution:
The two figures given are cylinder and cube.
Both figures are alike in respect of their same height.
Cylinder: d = 1 cm, h = 7 cm
Cube: Length of each side a = 7 cm
Both of the figures are different in respect of their shapes.
Lateral surface of cylinder = 2πrh
= 2 × 22/7 × 72 × 7 = 154 cm2
Lateral surface of the cube = 4l2 = 4 × (7)2 = 4 × 49 = 196
So, cube has the larger lateral surface = 196 cm2.
Question 7.
A closed cylindrical tank of radius 7 m and height 3 m is made from a sheet of metal. How many sheets of metal is required?
Solution:
Area of metal sheet required = Total surface area of the cylindrical tank = 2πr(h + r)
= 2 × 22/7 × 7(3 + 7)
= 2 × 22/7 × 7 × 10
= 440 m2
Hence, the required area of sheet = 440 m2.
Question 8.
The lateral surface area of a hollow cylinder is 4224 cm2. It is cut along its height and formed a rectangular sheet of width 33 cm. Find the perimeter of the rectangular sheet.
Solution:
Width of the rectangular sheet = Circumference of the cylinder

h = 128 cm
l = 128 cm, b = 33 cm
Perimeter of the sheet = 2(l + b) = 2(128 + 33) = 2 × 161 = 322 cm
Hence, the required perimeter = 322 cm.
Question 9.
A road roller takes 750 complete revolutions to move once over to level a road. Find the area of the road if the diameter of a road roller is 84 cm and length is 1 m.
Solution:
The lateral surface area of the road roller = 2πrh
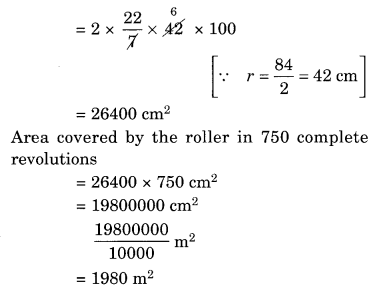
Hence, the area of road = 1980 m2
Question 10.
A company packages its milk powder in a cylindrical container whose base has a diameter of 14 cm and height 20 cm. The company places a label around the surface of the container (as shown in the figure). If the label is placed 2 cm from top and bottom, what is the area of the label?
Solution:
Here, r = 14/2 = 7 cm
Height of the cylindrical label = 20 – (2 + 2) = 16 cm
Surface area of the cylindrical shaped label = 2πrh
= 2 × 22/7 × 7 × 16
= 704 cm2
Hence, the required area of label = 704 cm2.
Exercise 11.4
Question 1.
Given a cylindrical tank, in which situation will you find the surface area and in which situation volume
(a) To find how much it can hold.
(b) Number of cement bags required to plaster it.
(c) To find the number of smaller tanks that can be filled with water from it.
Solution:
(a) In this situation, we can find the volume.
(b) In this situation, we can find the surface area.
(c) In this situation, we can find the volume.
Question 2.
Diameter of cylinder A is 7 cm, and the height is 14 cm. Diameter of cylinder B is 14 cm and height is 7 cm. Without doing any calculations can you suggest whose volume is greater? Verify it by finding the volume of both the cylinders. Check whether the cylinder with greater volume also has greater surface area?
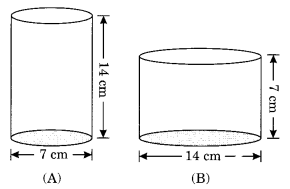
Solution:
Cylinder B has a greater volume.
Verification:
Volume of cylinder A = πr2h

Question 3.
Find the height of a cuboid whose base area is 180 cm2 and volume is 900 cm3.
Solution:
Given: Area of base = lb = 180 cm2
V = 900 cm3
Volume of the cuboid = l × b × h
900 = 180 × h
h = 5 cm
Hence, the required height = 5 cm.
Question 4.
A cuboid is of dimensions 60 cm × 54 cm × 30 cm. How many small cubes with side 6 cm can be placed in the given cuboid?
Solution:
Volume of the cuboid = l × b × h = 60 cm × 54 cm × 30 cm = 97200 cm3
Volume of the cube = (Side)3 = (6)3 = 216 cm3
Number of the cubes from the cuboid

Hence, the required number of cubes = 450.
Question 5.
Find the height of the cylinder whose volume is 1.54 m3 and the diameter of the base is 140 cm.
Solution:
V = 1.54 m3, d = 140 cm = 1.40 m
Volume of the cylinder = πr2h
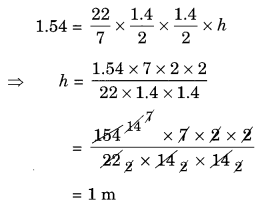
Hence, the height of cylinder = 1 m.
Question 6.
A milk tank is in the form of a cylinder whose radius is 1.5 m and length is 7 m. Find the quantity of milk in litres that can be stored in the tank.
Solution:
Here, r = 1.5 m
h = 7 m
.’. Volume of the milk tank = πr2h
= 22/7 × 1.5 × 1.5 × 7
= 22 × 2.25
= 49.50 m3
Volume of milk in litres = 49.50 × 1000 L (∵ 1 m3 = 1000 litres)
= 49500 L
Hence, the required volume = 49500 L.
Question 7.
If each edge of a cube is doubled,
(i) how many times will it be surface area increase?
(ii) how many times will its volume increase?
Solution:
Let the edge of the cube = x cm
If the edge is doubled, then the new edge = 2x cm
(i) Original surface area = 6x2 cm2
New surface area = 6(2x)2 = 6 × 4x2 = 24x2
Ratio = 6x2 : 24x2 = 1 : 4
Hence, the new surface area will be four times the original surface area.
(ii) Original volume of the cube = x3 cm3
New volume of the cube = (2x)3 = 8x3 cm3
Ratio = x3 : 8x3 = 1 : 8
Hence, the new volume will be eight times the original volume.
Question 8.
Water is pouring into a cuboidal reservoir at the rate of 60 litres per minute. If the volume of the reservoir is 108 m3, find the number of hours it will take to fill the reservoir.
Solution:
Volume of the reservoir = 108 m3 = 108000 L [∵1 m3 = 1000 L]
Volume of water flowing into the reservoir in 1 minute = 60 L
Time taken to fill the reservoir

Hence, the required hour to fill the reservoir = 30 hours.


