Exercise 7.1
Question 1.
Which of the following numbers are not perfect cubes?
(i) 216
(ii) 128
(iii) 1000
(iv) 100
(v) 46656
Solution:
(i) Prime factorisation of 216 is:
216 = 2 × 2 × 2 × 3 × 3 × 3
In the above factorisation, 2 and 3 have formed a group of three.
Thus, 216 is a perfect cube.

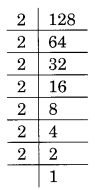
(ii) Prime factorisation of 128 is:
128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
Here, 2 is left without making a group of three.
Thus 128 is not a perfect cube.
(iii) Prime factorisation of 1000, is:
1000 = 2 × 2 × 2 × 5 × 5 × 5
Here, no number is left for making a group of three.
Thus, 1000 is a perfect cube.

(iv) Prime factorisation of 100, is:
100 = 2 × 2 × 5 × 5
Here 2 and 5 have not formed a group of three.
Thus, 100 is not a perfect cube.

(v) Prime factorisation of 46656 is:
46656 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3
Here 2 and 3 have formed the groups of three.
Thus, 46656 is a perfect cube.

Question 2.
Find the smallest number by which each of the following numbers must be multiplied to obtain a perfect cube.
(i) 243
(ii) 256
(iii) 72
(iv) 675
(v) 100
Solution:
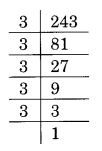
(i) Prime factorisation of 243, is:
243 = 3 × 3 × 3 × 3 × 3 = 33 × 3 × 3
Here, number 3 is required to make 3 × 3 a group of three, i.e., 3 × 3 × 3
Thus, the required smallest number to be multiplied is 3.
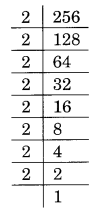
(ii) Prime factorisation of 256, is:
256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 23 × 23 × 2 × 2
Here, a number 2 is needed to make 2 × 2 a group of three, i.e., 2 × 2 × 2
Thus, the required smallest number to be multiplied is 2.
(iii) Prime factorisation of 72, is:
72 = 2 × 2 × 2 × 3 × 3 = 23 × 3 × 3
Here, a number 3 is required to make 3 × 3 a group of three, i.e. 3 × 3 × 3
Thus, the required smallest number to be multiplied is 3.

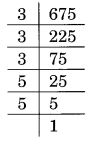
(iv) Prime factorisation of 675, is:
675 = 3 × 3 × 3 × 5 × 5 = 33 × 5 × 5
Here, a number 5 is required to make 5 × 5 a group of three to make it a perfect cube, i.e. 5 × 5 × 5
Thus, the required smallest number is 5.
(v) Prime factorisation of 100, is:
100 = 2 × 2 × 5 × 5
Here, number 2 and 5 are needed to multiplied 2 × 2 × 5 × 5 to make it a perfect cube, i.e., 2 × 2 × 2 × 5 × 5 × 5
Thus, the required smallest number to be multiplied is 2 × 5 = 10.

Question 3.
Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube.
(i) 81
(ii) 128
(iii) 135
(iv) 92
(v) 704
Solution:
(i) Prime factorisation of 81, is:
81 = 3 × 3 × 3 × 3 = 33 × 3
Here, a number 3 is the number by which 81 is divided to make it a perfect cube,
i.e., 81 ÷ 3 = 27 which is a perfect cube.
Thus, the required smallest number to be divided is 3.
(ii) Prime factorisation of 128, is:
128 = 2 × 2 × 2 × 2 × 2 × 2 × 2 = 23 × 23 × 2
Here, a number 2 is the smallest number by which 128 is divided to make it a perfect cube,
i.e., 128 ÷ 2 = 64 which is a perfect cube.
Thus, 2 is the required smallest number.
(iii) Prime factorisation of 135 is:
135 = 3 × 3 × 3 × 5 = 33 × 5
Here, 5 is the smallest number by which 135 is divided to make a perfect cube,
i.e., 135 ÷ 5 = 27 which is a perfect cube.
Thus, 5 is the required smallest number.
(iv) Prime factorisation of 192 is:
192 = 2 × 2 × 2 × 2 × 2 × 2 × 3 = 23 × 23 × 3
Here, 3 is the smallest number by which 192 is divided to make it a perfect cube,
i.e., 192 ÷ 3 = 64 which is a perfect cube.
Thus, 3 is the required smallest number.
(v) Prime factorisation of 704 is:
704 = 2 × 2 × 2 × 2 × 2 × 2 × 11 = 23 × 23 × 11
Here, 11 is the smallest number by which 704 is divided to make it a perfect cube,
i.e., 704 ÷ 11 = 64 which is a perfect cube.
Thus, 11 is the required smallest number.
Question 4.
Parikshit makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will be needed to form a cube?
Solution:
The sides of the cuboid are given as 5 cm, 2 cm and 5 cm.
Volume of the cuboid = 5 cm × 2 cm × 5 cm = 50 cm3
For the prime factorisation of 50, we have
50 = 2 × 5 × 5
To make it a perfect cube, we must have
2 × 2 × 2 × 5 × 5 × 5
= 20 × (2 × 5 × 5)
= 20 × volume of the given cuboid
Thus, the required number of cuboids = 20.
Exercise 7.2
Question 1.
Find the cube root of each of the following numbers by prime factorisation method.
(i) 64
(ii) 512
(iii) 10648
(iv) 27000
(v) 15625
(vi) 13824
(vii) 110592
(viii) 46656
(ix) 175616
(x) 91125
Solution:







Question 2.
State True or False.
(i) Cube of an odd number is even.
(ii) A perfect cube does not end with two zeros.
(iii) If the square of a number ends with 5, then its cube ends with 25.
(iv) There is no perfect cube which ends with 8.
(v) The cube of a two digit number may be a three digit number.
(vi) The cube of a two digit number may have seven or more digits.
(vii) The cube of a single digit number may be a single digit number.
Solution:
(i) False – Cube of any odd number is always odd, e.g., (7)3 = 343
(ii) True – A perfect cube does not end with two zeros.
(iii) True – If a square of a number ends with 5, then its cube ends with 25, e.g., (5)2 = 25 and (5)3 = 625
(iv) False – (12)3 = 1728 (ends with 8)
(v) False – (10)3 = 1000 (4-digit number)
(vi) False – (99)3 = 970299 (6-digit number)
(vii) True – (2)3 = 8 (1-digit number)


