Exercise 8.1
Question 1.
Find the ratio of the following:
(a) speed of a cycle 15 km per hour to the speed of scooter 30 km per hour.
(b) 5 m to 10 km
(c) 50 paise to ₹ 5
Solution:
(a) Speed of cycle : Speed of Scooter = 15 km per hour : 30 km per hour
Hence, the ratio = 1 : 2
(b) 5 m to 10 km
= 5 m : 10 × 1000 m [∵ 1 km = 1000 m]
= 5 m : 10000 m
= 1 : 2000
Hence, the ratio = 1 : 2000
(c) 50 paise to ₹ 5
= 50 paise : 5 × 100 paise
= 50 paise : 500 paise
ratio = 1 : 10
Question 2.
Convert the following ratios to percentages:
(a) 3 : 4
(b) 2 : 3
Solution:
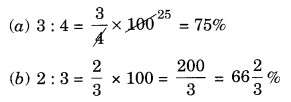
Question 3.
72% of 25 students are good in mathematics. How many are not good in mathematics?
Solution:
Number of students who are good in mathematics = 72% of 25
Number of students who are not good in mathematics = 25 – 18 = 7
Question 4.
A football team won 10 matches out of the total number of matches they played. If their win percentage was 40, then how many matches did they play in all?
Solution:
40 matches the team won out of 100 matches
1 match was won out of 100/40 matches
10 matches the team will won out of 100/40 × 10 = 25 matches
Hence, the total number of matches played by the team = 25
Question 5.
If Chameli had ₹ 600 left after spending 75% of her money, how much did she have in the beginning?
Solution:
Let the money with Chameli be ₹ 100
Money spent by her = 75% of 100 = ₹ 75
The money left with her = ₹ 100 – ₹ 75 = ₹ 25
₹ 25 are left with her out of ₹ 100
₹ 1 is left with her out of ₹ 100/25
₹ 600 will be left out of ₹ 100/25 × 600 = ₹ 2400
Hence, she had ₹ 2400 in beginning.
Question 6.
If 60% of people in a city like a cricket, 30% like football and the remaining like other games, then what per cent of the people like other games? If the total number of people are 50 lakh, find the exact number who like each type of game.
Solution:
Total number of people = 50,00,000
Number of people who like cricket = 60% of 50,00,000 = 30,00,000
Number of people who like football = 30% of 50,00,000 = 15,00,000
Number of people who like other games = 50,00,000 – (30,00,000 + 15,00,000)
= 50,00,000 – 45,00,000
= 5,00,000
Percentage of the people who like other games = 500000/5000000 × 100 = 10%
Hence, 10% of people like other game.
Exercise 8.2
Question 1.
A man got a 10% increase in his salary. If his new salary is ₹ 1,54,000, find his original salary.
Solution:
The increased salary = ₹ 1,54,000
Increase in salary = 10%
Increase salary = Original salary × (1 + Increase/100)
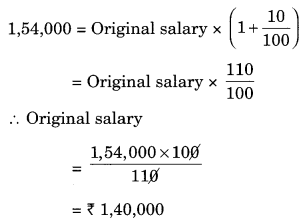
Hence, the original salary = ₹ 1,40,000
Question 2.
On Sunday 845 people went to the Zoo. On Monday only 169 people went. What is the per cent decrease in the people visiting the Zoo on Monday?
Solution:
Number of people visiting the Zoo on Sunday = 845
Number of people visiting the Zoo on Monday = 169
Decrease in number of people visiting the Zoo = 845 – 169 = 676
Decrease per cent
Hence, the decrease per cent = 80%
Question 3.
A shopkeeper buys 80 articles for ₹ 2,400 and sells them for a profit of 16%. Find the selling price of one article.
Solution:
Cost price of 80 articles = ₹ 2,400
Cost of 1 article = ₹ 2400/80 = ₹ 30
Profit = 16%
Hence, the selling price of one article = ₹ 34.80
Question 4.
The cost of an article was ₹ 15,500. ₹ 450 were spent on its repairs. If it is sold for a profit of 15%, find the selling price of the article.
Solution:
CP of the article = ₹ 15,500
Money spent on repairs = ₹ 450
Net CP = ₹ 15,500 + ₹ 450 = ₹ 15,950
Profit = 15%
Question 5.
A VCR and TV were bought for ₹ 8,000 each. The shopkeeper made a loss of 4% on the VCR and a profit of 8% on the TV. Find the gain or loss per cent on the whole transaction.
Solution:
Cost price of a VCR = ₹ 8,000
Loss = 4%
Hence, the shopkeeper gained 2% profit on the whole transaction.
Question 6.
During a sale, a shop offered a discount of 10% on the marked prices of all the items. What would a customer have to pay for a pair of Jeans marked at ₹ 1450 and two shirts marked at ₹ 850 each?
Solution:
Marked Price (MP) of Jeans = ₹ 1,450
MP of two shirts = ₹ 850 × 2 = ₹ 1,700
Total MP = ₹ 1,450 + ₹ 1,700 = ₹ 3,150
Discount = 10%
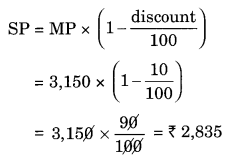
Thus, the customer will have to pay ₹ 2,835.
Question 7.
A milkman sold two of his buffaloes for ₹ 20,000 each. On one he made a gain of 5% and on the other a loss of 10%. Find his overall gain or loss. [Hint: Find CP of each]
Solution:
SP of a buffalo = ₹ 20,000
Gain = 5%
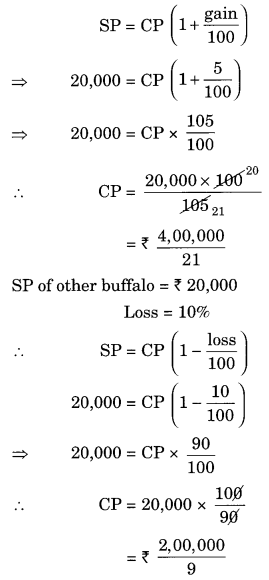
Question 8.
The price of a TV is ₹ 13,000. The sales tax charged on it is at the rate of 12%. Find the amount that Vinod will have to pay if he buys it.
Solution:
Marked price of the TV = ₹ 13,000
ST = 12%
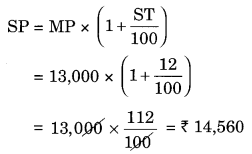
The required amount that Vinod has to pay = ₹ 14,560
Question 9.
Arun bought a pair of skates at a sale where the discount is given was 20%. If the amount he pays is ₹ 1,600, find the marked price.
Solution:
Let the MP of the skates be ₹ 100
Discount = ₹ 20% of 100 = ₹ 20
Sale price = ₹ 100 – ₹ 20 = ₹ 80
If SP is ₹ 80 then MP = ₹ 100
If SP is ₹ 1 then MP = ₹ 100/80
If SP is ₹ 1,600 then MP = ₹ 100/80 × 1600 = ₹ 2,000
Thus the MP = ₹ 2000.
Question 10.
I purchased a hair-dryer for ₹ 5,400 including 8% VAT. Find the price before VAT was added.
Solution:
Let the original price be ₹ 100
VAT = 8% of 100 = ₹ 8
Sale price = ₹ 100 + ₹ 8 = ₹ 108
If SP is ₹ 108 then original price = ₹ 100
If SP is ₹ 1 then the original price = ₹ 100/108
If SP is ₹ 5,400 then the original price = ₹ 100/108 × 5,400 = ₹ 5,000
Thus, the price of hair-dryer before the addition of VAT = ₹ 5000.
Exercise 8.3
Question 1.
Calculate the amount and compound interest on
(a) ₹ 10,800 for 3 years at 
% per annum compounded annually.
(b) ₹ 18,000 for 
years at 10% per annum compounded annually.
(c) ₹ 62,500 for 
years at 8% per annum compounded half yearly.
(d) ₹ 8,000 for 1 year at 9% per annum compounded half yearly. (You could use the year by year calculation using SI formula to verify).
(e) ₹ 10,000 for 1 year at 8% per annum compounded half yearly.
Solution:
(a) Given:
P = ₹ 10,800, n = 3 years,
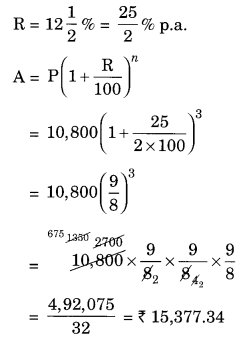
CI = A – P = ₹ 15,377.35 – ₹ 10,800 = ₹ 4,577.35
Hence amount = ₹ 15,377.34 and CI = ₹ 4,577.34
(b) Given: P = ₹ 18,000, n = years = 5/2 years
R = 10% p.a.
The amount for years, i.e., 2 years and 6 months can be calculated by first calculating the amount to 2 years using CI formula and then calculating the simple interest by using SI formula.
The amount for 2 years has to be calculated
Total CI = ₹ 3780 + ₹ 1089 = ₹ 4,869
Amount = P + I = ₹ 21,780 + ₹ 1,089 = ₹ 22,869
Hence, the amount = ₹ 22,869
and CI = ₹ 4,869
(c) Given: P = ₹ 62,500, n = years = 3/2 years per annum compounded half yearly
= 3/2 × 2 years = 3 half years
R = 8% = 8/2% = 4% half yearly
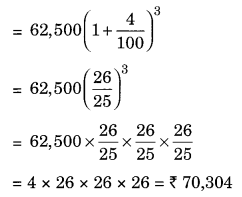
CI = A – P = ₹ 70,304 – ₹ 62,500 = ₹ 7,804
Hence, amount = ₹ 70304 and CI = ₹ 7804
(d) Given: P = ₹ 8,000, n = 1 years R = 9% per annum compounded half yearly
Since, the interest is compounded half yearly n = 1 × 2 = 2 half years
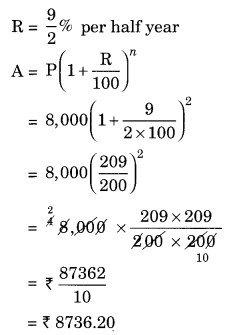
CI = A – P = ₹ 8,736.20 – ₹ 8,000 = ₹ 736.20
Hence, the amount = ₹ 8736.20 and CI = ₹ 736.20
(e) Given: P = ₹ 10,000, n = 1 year and R = 8% pa compounded half yearly
Since the interest is compounded half yearly n = 1 × 2 = 2 half years
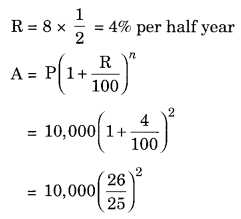
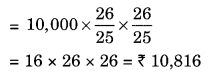
CI = A – P = ₹ 10,816 – ₹ 10,000 = ₹ 816
Hence the amount = ₹ 10,816 and Cl = ₹ 816
Question 2.
Kamala borrowed ₹ 26,400 from a Bank to buy a scooter at a rate of 15% per annum compounded yearly. What amount will she pay at the end of 2 years and 4 months to clear the loan? (Hint: Find amount for 2 years with interest is compounded yearly and then find SI on the 2nd
year amount for 4/12 years).
Solution:
Given:
P = ₹ 26,400
R = 15% p.a. compounded yearly
n = 2 years and 4 months
Amount after 2 years and 4 months = ₹ 34,914 + ₹ 1745.70 = ₹ 36,659.70
Hence, the amount to be paid by Kamla = ₹ 36,659.70
Question 3.
Fabina borrows ₹ 12,500 at 12% per annum for 3 years at simple interest and Radha borrows the same amount for the same time period at 10% per annum, compounded annually. Who pays more interest and by how much?
Solution:
For Fabina: P = ₹ 12,500, R = 12% p.a. and n = 3 years
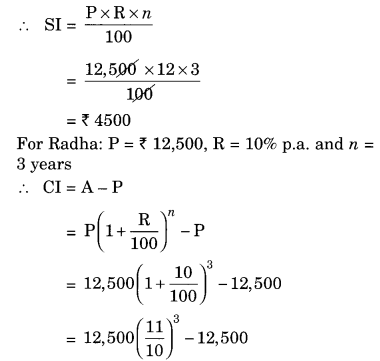
Difference between the two interests = ₹ 4500 – ₹ 4137.50 = ₹ 362.50
Hence, Fabina pays more interest by ₹ 362.50.
Question 4.
I borrowed ₹ 12,000 from Jamshed at 6% per annum simple interest for 2 years. Had I borrowed this sum at 6% per annum compound interest, what extra amount would I have to pay?
Solution:
Given: P = ₹ 12,000, R = 6% p.a., n = 2 years
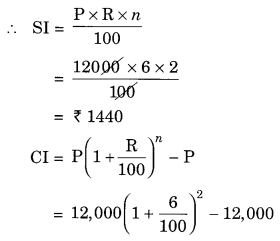
Difference between two interests = ₹ 1483.20 – ₹ 1440 = ₹ 43.20
Hence, the extra amount to be paid = ₹ 43.20
Ex 8.3 Class 8 Maths Question 5.
Vasudevan invested ₹ 60,000 at an interest rate of 12% per annum compounded half yearly. What amount would he get
(i) after 6 months?
(ii) after 1 year?
Solution:
(i) Given: P = ₹ 60,000, R = 12% p.a. compounded half yearly
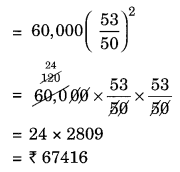
Ex 8.3 Class 8 Maths Question 6.
Arif took a loan of ₹ 80,000 from a bank. If the rate of interest is 10% per annum, find the difference in amounts he would be paying after
112 years if the interest is
(i) compounded annually.
(ii) compounded half yearly.
Solution:
(i) Given: P = ₹ 80,000
R = 10% p.a.
n = 112 years
Since the interest is compounded annually
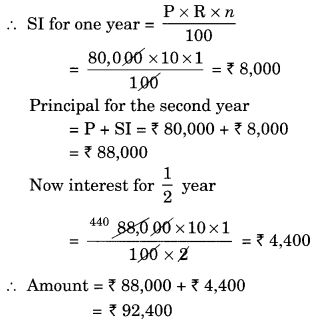
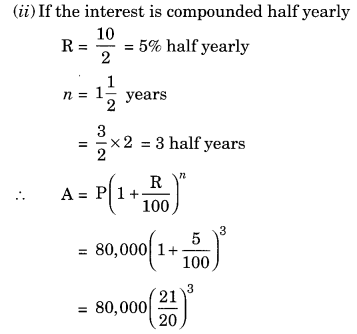
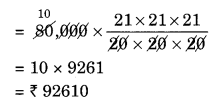
Difference between the amounts = ₹ 92,610 – ₹ 92,400 = ₹ 210
Ex 8.3 Class 8 Maths Question 7.
Maria invested ₹ 8,000 in a business. She would be paid interest at 5% per annum compounded annually. Find
(i) The amount credited against her name at the end of the second year.
(ii) The interest for the third year.
Solution:
(i) Given: P = ₹ 8,000, R = 5% p.a.
and n = 2 years
Hence, interest for the third year = ₹ 441
Ex 8.3 Class 8 Maths Question 8.
Find the amount and the compound interest on ₹ 10,000 for 112 years at 10% per annum, compounded half yearly. Would this interest be more than the interest he would get if it was compounded annually?
Solution:
Given: P = ₹ 10,000, n = 112 years
R = 10% per annum
Since the interest is compounded half yearly
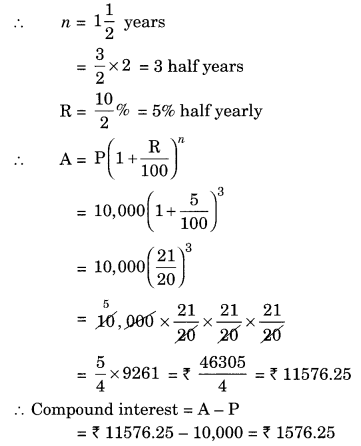
Total interest = ₹ 1,000 + ₹ 550 = ₹ 1,550
Difference between the two interests = ₹ 1,576.25 – ₹ 1,550 = ₹ 26.25
Hence, the interest will be ₹ 26.25 more when compounded half yearly than the interest when compounded annually.
Ex 8.3 Class 8 Maths Question 9.
Find the amount which Ram will get on ₹ 4,096, if he gave it for 18 months at 1212 per annum, interest being compounded half yearly.
Solution:
Given: P = ₹ 4,096, R = 1212 % pa, n = 18 months
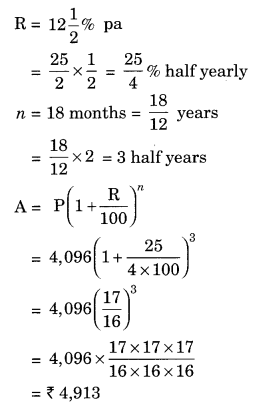
Hence, the required amount = ₹ 4913
Ex 8.3 Class 8 Maths Question 10.
The population of a place increased to 54,000 in 2003 at a rate of 5% per annum.
(i) Find the population in 2001.
(ii) What would be its population in 2005?
Solution:
(i) Given: Population in 2003 = 54,000
Rate = 5% pa
Time = 2003 – 2001 = 2 years
Population in 2003 = Population in 2001
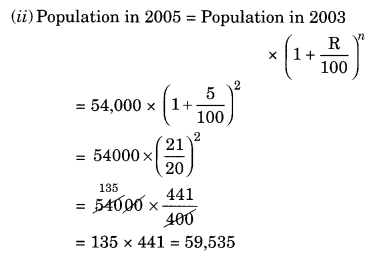
Ex 8.3 Class 8 Maths Question 11.
In a Laboratory, the count of bacteria in a certain experiment was increasing at the rate of 2.5% per hour. Find the bacteria at the end of 2 hours if the count was initially 5,06,000.
Solution:
Given: Initial count of bacteria = 5,06,000
Rate = 2.5% per hour
n = 2 hours
Number of bacteria at the end of 2 hours = Number of count of bacteria initially
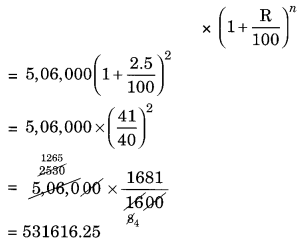
Thus, the number of bacteria after two hours = 5,31,616 (approx).
Ex 8.3 Class 8 Maths Question 12.
A scooter was bought at ₹ 42,000. Its value depreciated at the rate of 8% per annum. Find its value after one year.
Solution:
Given: Cost price of the scooter = ₹ 42,000
Rate of depreciation = 8% p.a.
Time = 1 year
Final value of the scooter
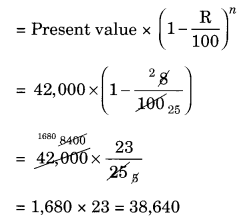
Hence, the value of scooter after 1 year = ₹ 38,640.
