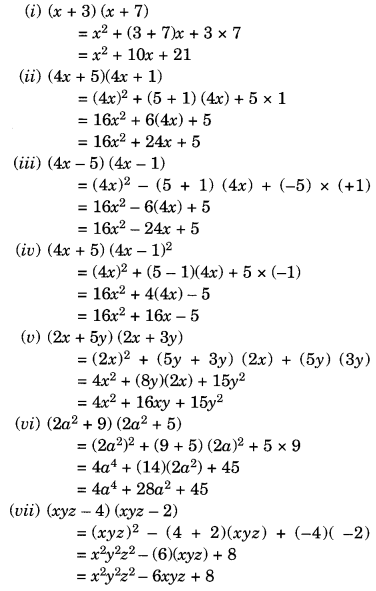Exercise 9.1
Question 1.
Identify the terms, their coefficients for each of the following expressions.
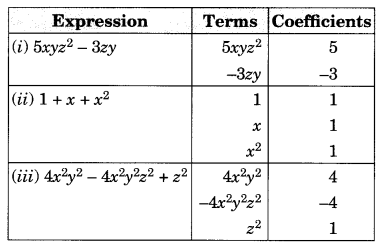
(i) 5xyz2 – 3zy
(ii) 1 + x + x2
(iii) 4x2y2 – 4x2y2z2 + z2
(iv) 3 – pq + qr – rp
(v) x/2+ y/2 – xy
(vi) 0.3a – 0.6ab + 0.5b
Solution:
Question 2.
Classify the following polynomials as monomials, binomials, trinomials. Which polynomials do not fit in any of these three categories?
x + y, 1000, x + x2 + x3 + x4, 7 + y + 5x, 2y – 3y2, 2y – 3y2 + 4y3, 5x – 4y + 3xy, 4z – 15z2, ab + bc + cd + da, pqr, p2q + pq2, 2p + 2q
Solution:

Question 3.
Add the following:
(i) ab – bc, bc – ca, ca – ab
(ii) a – b + ab, b – c + bc, c – a + ac
(iii) 2p2q2 – 3pq + 4, 5 + 7pq – 3p2q2
(iv) l2 + m2, m2 + n2, n2 + l2, 2lm + 2mn + 2nl
Solution:
(i) Given: ab – bc, bc – ca, ca – ab
We have
(ab – bc) + (bc – ca) + (ca – ab) (Adding all the terms)
= ab – bc + bc – ca + ca – ab
= (ab – ab) + (bc – bc) + (ca – ca) (Collecting the like terms together)
= 0 + 0 + 0
= 0
(ii) Given:
a – b + ab, b – c + bc, c – a + ac
We have (a – b + ab) + (b – c + bc) + (c – a + ac) (Adding all the terms)
= a – b + ab + b – c + bc + c – a + ac
= (a – a) + (b – b) + (c – c) + ab + bc + ac (Collecting all the like terms together)
= 0 + 0 + 0 + ab + bc + ac
= ab + bc + ac
(iii) Given:
2p2q2 – 3pq + 4, 5 + 7pq – 3p2q2
By arranging the like terms in the same column, we have
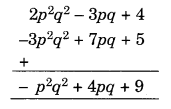
(iv) Given: l2 + m2, m2 + n2, n2 + l2, 2lm + 2mn + nl

Thus, the sum of the given expressions is 2(l2 + m2 + n2 + lm + mn + nl)
Question 4.
(a) Subtract 4a – 7ab + 3b + 12 from 12a – 9ab + 5b – 3
(b) Subtract 3xy + 5yz – 7zx from 5xy – 2yz – 2zx + 10xyz
(c) Subtract 4p2q – 3pq + 5pq2 – 8p + 7q – 10 from 18 – 3p – 11q + 5pq – 2pq2 + 5p2q
Solution:
(a) Arranging the like terms column-wise, we have
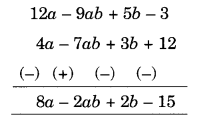
(b) Subtract 3xy + 5yz – 7zx from 5xy – 2yz – 2zx + 10xyz
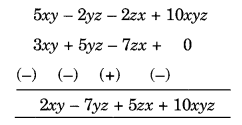
(c) Subtract 4p2q – 3pq + 5pq2 – 8p + 7q – 10 from 18 – 3p – 11q + 5pq – 2pq2 + 5p2q
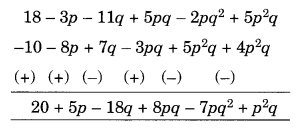
The terms are p2q – 7pq2 + 8pq – 18q + 5p + 20
Exercise 9.2
Question 1.
Find the product of the following pairs of monomials.
(i) 4, 7p
(ii) -4p, 7p
(iii) -4p, 7pq
(iv) 4p3, -3p
(v) 4p, 0
Solution:
(i) 4 × 7p = (4 × 7) × p = 28p
(ii) -4p × 7p = (-4 × 7) × p × p = -28p2
(iii) -4p × 7pq = (-4 × 7) × p × pq = -28p2q
(iv) 4p3 × -3p = (4 × -3) × p3 × p = -12p4
(v) 4p x 0 = (4 × 0) × p = 0 × p = 0
Question 2.
Find the areas of rectangles with the following pairs of monomials as their lengths and breadths respectively.
(p, q); (10m, 5n); (20x2, 5y2); (4x, 3x2); (3mn, 4np)
Solution:
(i) Length = p units and breadth = q units
Area of the rectangle = length × breadth = p × q = pq sq units
(ii) Length = 10 m units, breadth = 5n units
Area of the rectangle = length × breadth = 10 m × 5 n = (10 × 5) × m × n = 50 mn sq units
(iii) Length = 20x2 units, breadth = 5y2 units
Area of the rectangle = length × breadth = 20x2 × 5y2 = (20 × 5) × x2 × y2 = 100x2y2 sq units
(iv) Length = 4x units, breadth = 3x2 units
Area of the rectangle = length × breadth = 4x × 3x2 = (4 × 3) × x × x2 = 12x3 sq units
(v) Length = 3mn units, breadth = 4np units
Area of the rectangle = length × breadth = 3mn × 4np = (3 × 4) × mn × np = 12mn2p sq units
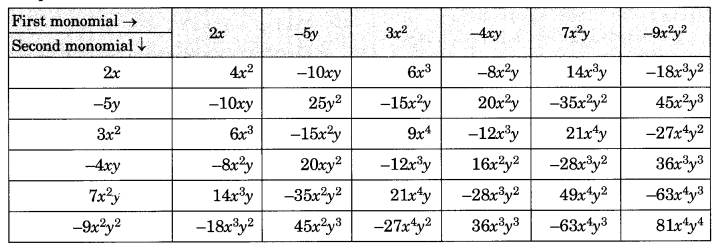
Question 3.
Complete the table of Products.
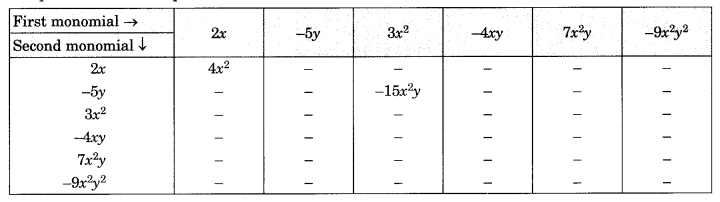
Solution:
Completed Table
Question 4.
Obtain the volume of rectangular boxes with the following length, breadth and height respectively.
(i) 5a, 3a2, 7a4
(ii) 2p, 4q, 8r
(iii) xy, 2x2y, 2xy2
(iv) a, 2b, 3c
Solution:
(i) Here, length = 5a, breadth = 3a2, height = 7a4
Volume of the box = l × b × h = 5a × 3a2 × 7a4 = 105 a7 cu. units
(ii) Here, length = 2p, breadth = 4q, height = 8r
Volume of the box = l × b × h = 2p × 4q × 8r = 64pqr cu. units
(iii) Here, length = xy, breadth = 2x2y, height = 2xy2
Volume of the box = l × b × h = xy × 2x2y × 2xy2 = (1 × 2 × 2) × xy × x2y × xy2 = 4x4y4 cu. units
(iv) Here, length = a, breadth = 2b, height = 3c
Volume of the box = length × breadth × height = a × 2b × 3c = (1 × 2 × 3)abc = 6 abc cu. units
Question 5.
Obtain the product of
(i) xy, yz, zx
(ii) a, -a2, a3
(iii) 2, 4y, 8y2, 16y3
(iv) a, 2b, 3c, 6abc
(v) m, -mn, mnp
Solution:
(i) xy × yz × zx = x2y2z2
(ii) a × (-a2) × a3 = -a6
(iii) 2 × 4y × 8y2 × 16y3 = (2 × 4 × 8 × 16) × y × y2 × y3 = 1024y6
(iv) a × 2b × 3c × 6abc = (1 × 2 × 3 × 6) × a × b × c × abc = 36 a2b2c2
(v) m × (-mn) × mnp = [1 × (-1) × 1 ]m × mn × mnp = -m3n2p
Exercise 9.3
Question 1.
Carry out the multiplication of the expressions in each of the following pairs:
(i) 4p, q + r
(ii) ab, a – b
(iii) a + b, 7a2b2
(iv) a2 – 9, 4a
(v) pq + qr + rp, 0
Solution:
(i) 4p × (q + r) = (4p × q) + (4p × r) = 4pq + 4pr
(ii) ab, a – b = ab × (a – b) = (ab × a) – (ab × b) = a2b – ab2
(iii) (a + b) × 7a2b2 = (a × 7a2b2) + (b × 7a2b2) = 7a3b2 + 7a2b3
(iv) (a2 – 9) × 4a = (a2 × 4a) – (9 × 4a) = 4a3 – 36a
(v) (pq + qr + rp) × 0 = 0
[∵ Any number multiplied by 0 is = 0]
Question 2.
Complete the table.
| S.No. | First Expression | Second Expression |
Product |
| (i) | a | b + c + d | – |
| (ii) | x + y – 5 | 5xy | – |
| (iii) | p | 6p2 – 7p + 5 | – |
| (iv) | 4p2q2 | p2 – q2 | – |
| (v) | a + b + c | abc | – |
Solution:
(i) a × (b + c + d) = (a × b) + (a × c) + (a × d) = ab + ac + ad
(ii) (x + y – 5) (5xy) = (x × 5xy) + (y × 5xy) – (5 × 5xy) = 5x2y + 5xy2 – 25xy
(iii) p × (6p2 – 7p + 5) = (p × 6p2) – (p × 7p) + (p × 5) = 6p3 – 7p2 + 5p
(iv) 4p2q2 × (p2 – q2) = 4p2q2 × p2 – 4p2q2 × q2 = 4p4q2 – 4p2q4
(v) (a + b + c) × (abc) = (a × abc) + (b × abc) + (c × abc) = a2bc + ab2c + abc2
Completed Table:
| S.No. | First Expression | Second Expression |
Product |
| (i) | a | b + c + d | ab + ac + ad |
| (ii) | x + y – 5 | 5xy | 5x2y + 5xy2 – 25xy |
| (iii) | p | 6p2 – 7p + 5 | 6p3 – 7p2 + 5p |
| (iv) | 4p2q2 | p2 – q2 | 4p4q2 – 4p2q4 |
| (v) | a + b + c | abc | a2bc + ab2c + abc2 |
Question 3.
Find the products.
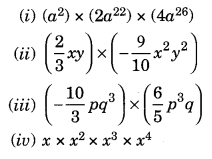
Solution:
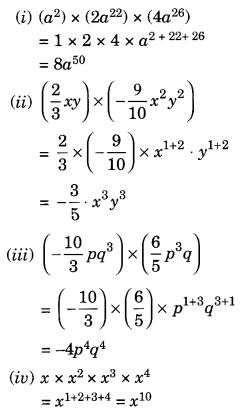
Question 4.
(a) Simplify: 3x(4x – 5) + 3 and find its values for (i) x = 3 (ii) x =![]()
(b) Simplify: a(a2 + a + 1) + 5 and find its value for (i) a = 0 (ii) a = 1 (iii) a = -1
Solution:
(a) We have 3x(4x – 5) + 3 = 4x × 3x – 5 × 3x + 3 = 12x2 – 15x + 3
(i) For x = 3, we have
12 × (3)2 – 15 × 3 + 3 = 12 × 9 – 45 + 3 = 108 – 42 = 66
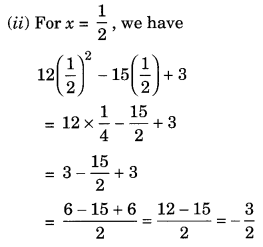
(b) We have a(a2 + a + 1) + 5
= (a2 × a) + (a × a) + (1 × a) + 5
= a3 + a2 + a + 5
(i) For a = 0, we have
= (0)3 + (0)2 + (0) + 5 = 5
(ii) For a = 1, we have
= (1)3 + (1)2 + (1) + 5 = 1 + 1 + 1 + 5 = 8
(iii) For a = -1, we have
= (-1)3 + (-1)2 + (-1) + 5 = -1 + 1 – 1 + 5 = 4
Question 5.
(a) Add: p(p – q), q(q – r) and r(r – p)
(b) Add: 2x(z – x – y) and 2y(z – y – x)
(c) Subtract: 3l(l – 4m + 5n) from 4l(10n – 3m + 2l)
(d) Subtract: 3a(a + b + c) – 2b(a – b + c) from 4c(-a + b + c)
Solution:
(a) p(p – q) + q(q – r) + r(r – p)
= (p × p) – (p × q) + (q × q) – (q × r) + (r × r) – (r × p)
= p2 – pq + q2 – qr + r2 – rp
= p2 + q2 + r2 – pq – qr – rp
(b) 2x(z – x – y) + 2y(z – y – x)
= (2x × z) – (2x × x) – (2x × y) + (2y × z) – (2y × y) – (2y × x)
= 2xz – 2x2 – 2xy + 2yz – 2y2 – 2xy
= -2x2 – 2y2 + 2xz + 2yz – 4xy
= -2x2 – 2y2 – 4xy + 2yz + 2xz
(c) 4l(10n – 3m + 2l) – 3l(l – 4m + 5n)
= (4l × 10n) – (4l × 3m) + (4l × 2l) – (3l × l) – (3l × -4m) – (3l × 5n)
= 40ln – 12lm + 8l2 – 3l2 + 12lm – 15ln
= (40ln – 15ln) + (-12lm + 12lm) + (8l2 – 3l2)
= 25ln + 0 + 5l2
= 25ln + 5l2
= 5l2 + 25ln
(d) [4c(-a + b + c)] – [3a(a + b + c) – 2b(a – b + c)]
= (-4ac + 4bc + 4c2) – (3a2 + 3ab + 3ac – 2ab + 2b2 – 2bc)
= -4ac + 4bc + 4c2 – 3a2 – 3ab – 3ac + 2ab – 2b2 + 2bc
= -3a2 – 2b2 + 4c2 – ab + 6bc – 7ac
Exercise 9.4
Question 1.
Multiply the binomials:
(i) (2x + 5) and (4x – 3)
(ii) (y – 8) and (3y – 4)
(iii) (2.5l – 0.5m) and (2.5l + 0.5m)
(iv) (a + 3b) and (x + 5)
(v) (2pq + 3q2) and (3pq – 2q2)
(vi) (¾ a2 + 3b2) and 4(a2 –2/3 b2)
Solution:
(i) (2x + 5) × (4x – 3)
= 2x × (4x – 3) + 5 × (4x – 3)
= (2x × 4x) – (3 × 2x) + (5 × 4x) – (5 × 3)
= 8x2 – 6x + 20x – 15
= 8x2 + 14x – 15
(ii) (y – 8) × (3y – 4)
= y × (3y – 4) – 8 × (3y – 4)
= (y × 3y) – (y × 4) – (8 × 3y) + (-8 × -4)
= 3y2 – 4y – 24y + 32
= 3y2 – 28y + 32
(iii) (2.5l – 0.5m) × (2.5l + 0.5m)
= (2.5l × 2.5l) + (2.5l × 0.5m) – (0.5m × 2.5l) – (0.5m × 0.5m)
= 6.25l2 + 1.25ml – 1.25ml – 0.25m2
= 6.25l2 + 0 – 0.25m2
= 6.25l2 – 0.25m2
(iv) (a + 3b) × (x + 5)
= a × (x + 5) + 36 × (x + 5)
= (a × x) + (a × 5) + (36 × x) + (36 × 5)
= ax + 5a + 3bx + 15b
(v) (2pq + 3q2) × (3pq – 2q2)
= 2pq × (3pq – 2q2) + 3q2 (3pq – 2q2)
= (2pq × 3pq) – (2pq × 2q2) + (3q2 × 3pq) – (3q2 × 2q2)
= 6p2q2 – 4pq3 + 9pq3 – 6q4
= 6p2q2 + 5pq3 – 6q4
Question 2.
Find the product:
(i) (5 – 2x) (3 + x)
(ii) (x + 7y) (7x – y)
(iii) (a2 + b) (a + b2)
(iv) (p2 – q2)(2p + q)
Solution:
(i) (5 – 2x) (3 + x)
= 5(3 + x) – 2x(3 + x)
= (5 × 3) + (5 × x) – (2x × 3) – (2x × x)
= 15 + 5x – 6x – 2x2
(ii) (x + 7y) (7x – y)
= x(7x – y) + 7y(7x – y)
= (x × 7x) – (x × y) + (7y × 7x) – (7y × y)
= 7x2 – xy + 49xy – 7y2
= 7x2 + 48xy – 7y2
(iii) (a2 + b) (a + b2)
= a2 (a + b2) + b(a + b2)
= (a2 × a) + (a2 × b2) + (b × a) + (b × b2)
= a3 + a2b2 + ab + b3
(iv) (p2 – q2)(2p + q)
= p2(2p + q) – q2(2p + q)
= (p2 × 2p) + (p2 × q) – (q2 × 2p) – (q2 × q)
= 2p3 + p2q – 2pq2 – q3
Question 3.
Simplify:
(i) (x2 – 5) (x + 5) + 25
(ii) (a2 + 5)(b3 + 3) + 5
(iii) (t + s2) (t2 – s)
(iv) (a + b) (c – d) + (a – b) (c + d) + 2(ac + bd)
(v) (x + y) (2x + y) + (x + 2y) (x – y)
(vi) (x + y)(x2 – xy + y2)
(vii) (1.5x – 4y)(1.5x + 4y + 3) – 4.5x + 12y
(viii) (a + b + c) (a + b – c)
Solution:
(i) (x2 – 5) (x + 5) + 25
= x2(x + 5) + 5(x + 5) + 25
= x3 + 5x2 – 5x – 25 + 25
= x3 + 5x2 – 5x + 0
= x3 + 5x2 – 5x
(ii) (a2 + 5)(b3 + 3) + 5
= a2(b3 + 3) + 5(b3 + 3) + 5
= a2b3 + 3a2 + 5b3 + 15 + 5
= a2b3 + 3a2 + 5b3 + 20
(iii) (t + s2) (t2 – s)
= t(t2 – s) + s2(t2 – s)
= t3 – st + s2t2 – s3
= t3 + s2t2 – st – s3
(iv) (a + b)(c – d) + (a – b) (c + d) + 2(ac + bd)
= a(c – d) + b(c – d) + a(c + d) – b(c + d) + 2ac + 2bd
= ac – ad + bc – bd + ac + ad – bc – bd + 2ac + 2bd
= ac + ac + 2ac + bc – bc – ad + ad – bd – bd + 2bd
= 4ac + 0 + 0 + 0
= 4ac
(v) (x + y) (2x + y) + (x + 2y) (x – y)
= x(2x + y) + y(2x + y) + x(x – y) + 2y(x – y)
= 2x2 + xy + 2xy + y2 + x2 – xy + 2xy – 2y2
= 2x2 + x2 + xy + 2xy – xy + 2xy + y2 – 2y2
= 3x2 + 4xy – y2
(vi) (x + y)(x2 – xy + y2)
= x(x2 – xy + y2) + y(x2 – xy + y2)
= x3 – x2y + x2y + xy2 – xy2 + y3
= x3 – 0 + 0 + y3
= x3 + y3
(vii) (1.5x – 4y)(1.5x + 4y + 3) – 4.5x.+ 12y
= 1.5x (1.5x + 4y + 3) – 4y(1.5x + 4y + 3) – 4.5x + 12y
= 2.25x2 + 6xy + 4.5x – 6xy – 16y2 – 12y – 4.5x + 12y
= 2.25x2 + 6xy – 6xy + 4.5x – 4.5x + 12y – 12y – 16y2
= 2.25x2 + 0 + 0 + 0 – 16y2
= 2.25x2 – 16y2
(viii) (a + b + c) (a + b – c)
= a(a + b – c) + b(a + b – c) + c(a + b – c)
= a2 + ab – ac + ab + b2 – bc + ac + bc – c2
= a2 + ab + ab – bc + bc – ac + ac + b2 – c2
= a2 + 2ab + b2 – c2 + 0 + 0
= a2 + 2ab + b2 – c2
Exercise 9.5
Question 1.
Use a suitable identity to get each of the following products:
(i) (x + 3) (x + 3)
(ii) (2y + 5) (2y + 5)
(iii) (2a – 7) (2a – 7)
(iv) (3a – ![]() ) (3a –
) (3a – ![]() )
)
(v) (1.1m – 0.4) (1.1m + 0.4)
(vi) (a2 + b2) (-a2 + b2)
(vii) (6x – 7) (6x + 7)
(viii) (-a + c) (-a + c)
(ix) ( +
) (
+
)
(x) (7a – 9b) (7a – 9b)
Solution:
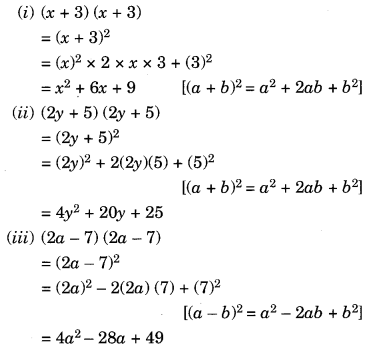
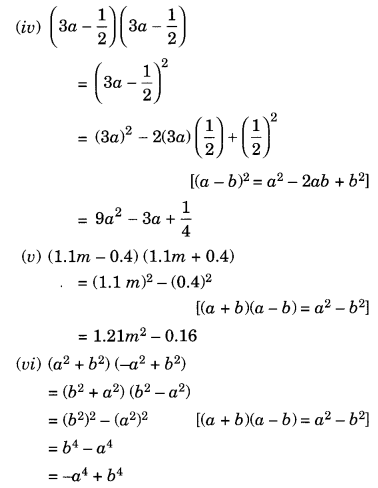
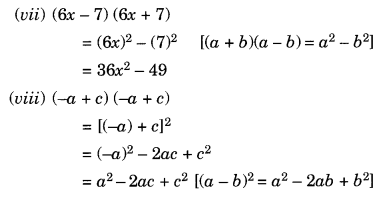
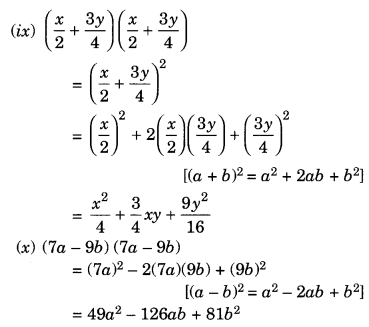
Question 2.
Use the identity (x + a)(x + b) = x2 + (a + b)x + ab to find the following products.
(i) (x + 3) (x + 7)
(ii) (4x + 5)(4x + 1)
(iii) (4x – 5) (4x – 1)
(iv) (4x + 5) (4x – 1)
(v) (2x + 5y) (2x + 3y)
(vi) (2a2 + 9) (2a2 + 5)
(vii) (xyz – 4) (xyz – 2)
Solution: