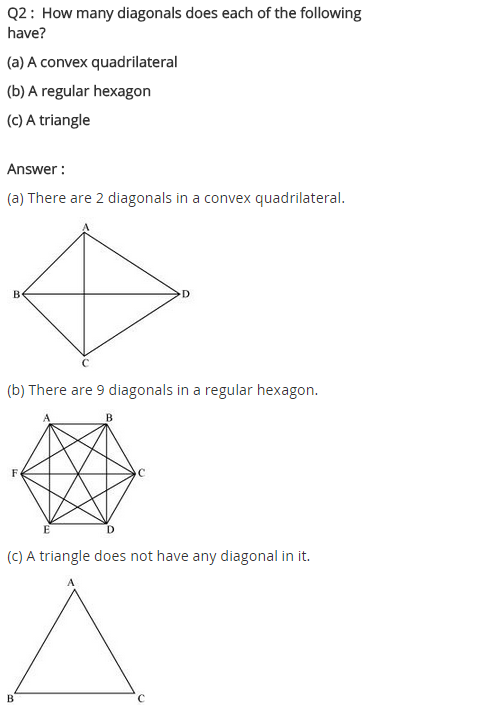
Exercise 3.1
1. Given here are some figures.

Classify each of them on the basis of the following.
Simple curve (b) Simple closed curve (c) Polygon
(d) Convex polygon (e) Concave polygon
Solution:
a) Simple curve: 1, 2, 5, 6 and 7
b) Simple closed curve: 1, 2, 5, 6 and 7
c) Polygon: 1 and 2
d) Convex polygon: 2
e) Concave polygon: 1




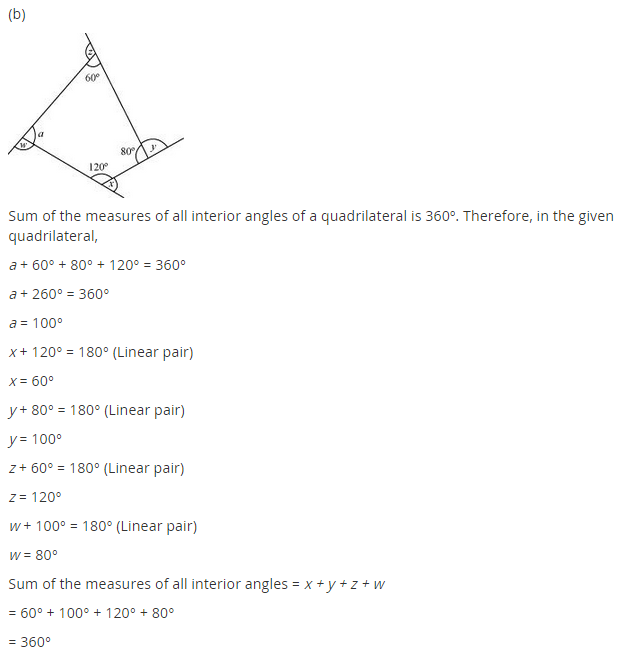
Exercise 3.2
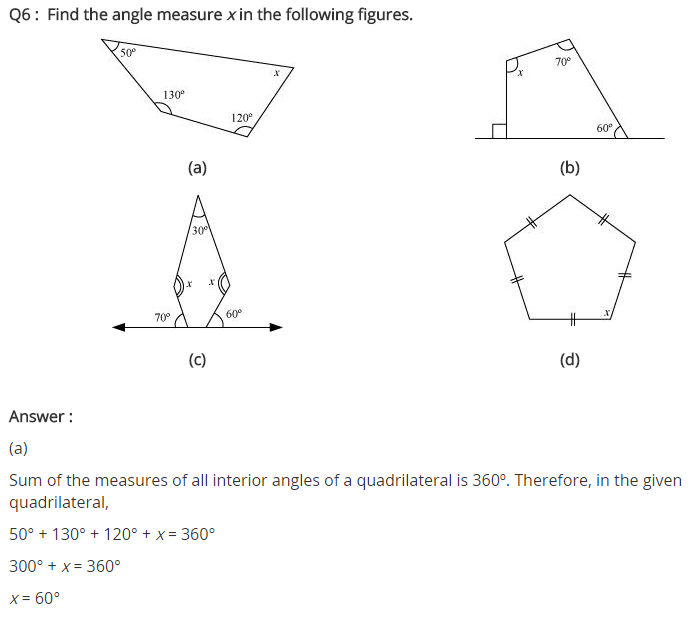
1. Find x in the following figures.
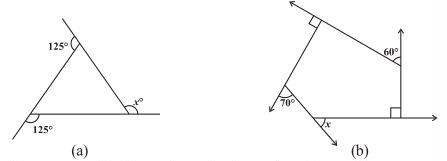
Solution:
a) 125° + m = 180° ⇒ m = 180° – 125° = 55° (Linear pair)
125° + n = 180° ⇒ n = 180° – 125° = 55° (Linear pair)
x = m + n (exterior angle of a triangle is equal to the sum of 2 opposite interior 2 angles)
⇒ x = 55° + 55° = 110°
b)
Two interior angles are right angles = 90°
70° + m = 180° ⇒ m = 180° – 70° = 110° (Linear pair)
60° + m = 180° ⇒ m = 180° – 60° = 120° (Linear pair) The figure is having five sides and is a pentagon.
Thus, sum of the angles of pentagon = 540° 90° + 90° + 110° + 120° + y = 540°
⇒ 410° + y = 540° ⇒ y = 540° – 410° = 130°
x + y = 180° (Linear pair)
⇒ x + 130° = 180°
⇒ x = 180° – 130° = 50°
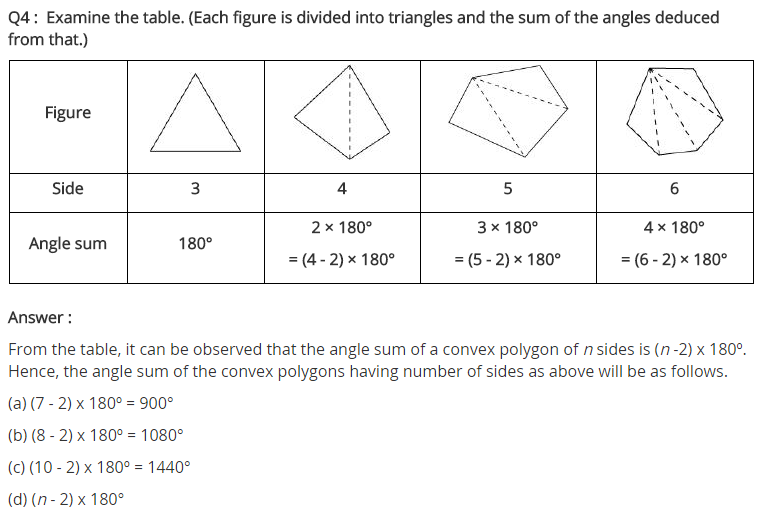
2. Find the measure of each exterior angle of a regular polygon of
(i) 9 sides (ii) 15 sides Solution:
Sum of angles a regular polygon having side n = (n-2)×180°
(i) Sum of angles a regular polygon having side 9 = (9-2)×180°= 7×180° = 1260°
Each interior angle=1260/9 = 140°
Each exterior angle = 180° – 140° = 40°
Or,
Each exterior angle = sum of exterior angles/Number of angles = 360/9 = 40°
(ii) Sum of angles a regular polygon having side 15 = (15-2)×180°
= 13×180° = 2340°
Each interior angle = 2340/15 = 156°
Each exterior angle = 180° – 156° = 24°
Or,
Each exterior angle = sum of exterior angles/Number of angles = 360/15 = 24°
3. How many sides does a regular polygon have if the measure of an exterior angle is 24°? Solution:
Each exterior angle = sum of exterior angles/Number of angles
24°= 360/ Number of sides
⇒ Number of sides = 360/24 = 15
Thus, the regular polygon has 15 sides.
4. How many sides does a regular polygon have if each of its interior angles is 165°?
Solution:
Interior angle = 165°
Exterior angle = 180° – 165° = 15°
Number of sides = sum of exterior angles/ exterior angles
⇒ Number of sides = 360/15 = 24
Thus, the regular polygon has 24 sides.
5. a) Is it possible to have a regular polygon with measure of each exterior angle as 22°?
b) Can it be an interior angle of a regular polygon? Why?
Solution:
a) Exterior angle = 22°
Number of sides = sum of exterior angles/ exterior angle
⇒ Number of sides = 360/22 = 16.36
No, we can’t have a regular polygon with each exterior angle as 22° as it is not divisor of 360.
b) Interior angle = 22°
Exterior angle = 180° – 22°= 158°
No, we can’t have a regular polygon with each exterior angle as 158° as it is not divisor of 360.
6. a) What is the minimum interior angle possible for a regular polygon? Why?
b) What is the maximum exterior angle possible for a regular polygon?
Solution:
a) Equilateral triangle is regular polygon with 3 sides has the least possible minimum interior angle because the regular with minimum sides can be constructed with 3 sides at least.. Since, sum of interior angles of a triangle = 180°
Each interior angle = 180/3 = 60°
b) Equilateral triangle is regular polygon with 3 sides has the maximum exterior angle because the regular polygon with least number of sides have the maximum exterior angle possible. Maximum exterior possible = 180 – 60° = 120°
Exercise 3.3
1. Given a parallelogram ABCD. Complete each statement along with the definition or property used.
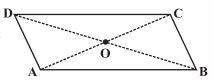
(i) AD = …… (ii) ∠DCB = ……
(iii) OC = …… (iv) m ∠DAB + m ∠CDA = ……
Solution:
(i) AD = BC (Opposite sides of a parallelogram are equal)
(ii) ∠DCB = ∠DAB (Opposite angles of a parallelogram are equal) (iii) OC = OA (Diagonals of a parallelogram are equal)
(iv) m ∠DAB + m ∠CDA = 180°
2. Consider the following parallelograms. Find the values of the unknown x, y, z

Solution:
(i)
y = 100° (opposite angles of a parallelogram)
x + 100° = 180° (Adjacent angles of a parallelogram)
⇒ x = 180° – 100° = 80°
x = z = 80° (opposite angles of a parallelogram)
∴, x = 80°, y = 100° and z = 80°
(ii)
50° + x = 180° ⇒ x = 180° – 50° = 130° (Adjacent angles of a parallelogram)
x = y = 130° (opposite angles of a parallelogram)
x = z = 130° (corresponding angle)
(iii)
x = 90° (vertical opposite angles)
x + y + 30° = 180° (angle sum property of a triangle)
⇒ 90° + y + 30° = 180°
⇒ y = 180° – 120° = 60°
also, y = z = 60° (alternate angles)
(iv)
z = 80° (corresponding angle)
z = y = 80° (alternate angles)
x + y = 180° (adjacent angles)
⇒ x + 80° = 180° ⇒ x = 180° – 80° = 100°
(v)
x=28o
y = 112o z = 28o
3. Can a quadrilateral ABCD be a parallelogram if (i) ∠D + ∠B = 180°?
(ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
(iii)∠A = 70° and ∠C = 65°?
Solution:
(i) Yes, a quadrilateral ABCD be a parallelogram if ∠D + ∠B = 180° but it should also
fulfilled some conditions which are:
(a) The sum of the adjacent angles should be 180°.
(b) Opposite angles must be equal.
(ii) No, opposite sides should be of same length. Here, AD ≠ BC
(iii) No, opposite angles should be of same measures. ∠A ≠ ∠C
4. Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measure.
Solution:
ABCD is a figure of quadrilateral that is not a parallelogram but has exactly two opposite
angles that is ∠B = ∠D of equal measure. It is not a parallelogram because ∠A ≠ ∠C.
5. The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
Solution:
Let the measures of two adjacent angles ∠A and ∠B be 3x and 2x respectively in
parallelogram ABCD.
∠A + ∠B = 180°
⇒ 3x + 2x = 180°
⇒ 5x = 180°
⇒ x = 36°
We know that opposite sides of a parallelogram are equal.
∠A = ∠C = 3x = 3 × 36° = 108°
∠B = ∠D = 2x = 2 × 36° = 72°
6. Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
Solution:
Let ABCD be a parallelogram.
Sum of adjacent angles of a parallelogram = 180°
∠A + ∠B = 180°
⇒ 2∠A = 180°
⇒ ∠A = 90°
also, 90° + ∠B = 180°
⇒ ∠B = 180° – 90° = 90°
∠A = ∠C = 90°
∠B = ∠D = 90
°
7. The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
Solution:
y = 40° (alternate interior angle)
∠P = 70° (alternate interior angle)
∠P = ∠H = 70° (opposite angles of a parallelogram)
z = ∠H – 40°= 70° – 40° = 30°
∠H + x = 180°
⇒ 70° + x = 180°
⇒ x = 180° – 70° = 110°
8. The following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm)
Solution:
(i) SG = NU and SN = GU (opposite sides of a parallelogram are equal) 3x = 18
x = 18/3
⇒ x =6
3y – 1 = 26 an
d,
⇒ 3y = 26 + 1
⇒ y = 27/3=9
x = 6 and y = 9
(ii) 20 = y + 7 and 16 = x + y (diagonals of a parallelogram bisect each other) y + 7 = 20
⇒ y = 20 – 7 = 13 and,
x + y = 16
⇒ x + 13 = 16
⇒ x = 16 – 13 = 3
x = 3 and y = 13
9. In the above figure both RISK and CLUE are parallelograms. Find the value of x.
Solution:
∠K + ∠R = 180° (adjacent angles of a parallelogram are supplementary)
⇒ 120° + ∠R = 180°
⇒ ∠R = 180° – 120° = 60°
also, ∠R = ∠SIL (corresponding angles)
⇒ ∠SIL = 60°
also, ∠ECR = ∠L = 70° (corresponding angles) x + 60° + 70° = 180° (angle sum of a triangle)
⇒ x + 130° = 180°
⇒ x = 180° – 130° = 50°
10. Explain how this figure is a trapezium. Which of its two sides are parallel? (Fig 3.32)
Solution:
When a transversal line intersects two lines in such a way that the sum of the adjacent angles on the same side of transversal is 180° then the lines are parallel to each other. Here, ∠M + ∠L = 100° + 80° = 180°
Thus, MN || LK
As the quadrilateral KLMN has one pair of parallel line therefore it is a trapezium. MN and LK are parallel lines.
11. Find m∠C in Fig 3.33 if AB || DC ?
Solution:
m∠C + m∠B = 180° (angles on the same side of transversal)
⇒ m∠C + 120° = 180°
⇒ m∠C = 180°- 120° = 60°
12. Find the measure of ∠P and ∠S if SP || RQ ? in Fig 3.34. (If you find m∠R, is there more than one
method to find m∠P?)
Solution:
∠P + ∠Q = 180° (angles on the same side of transversal)
⇒ ∠P + 130° = 180°
⇒ ∠P = 180° – 130° = 50°
also, ∠R + ∠S = 180° (angles on the same side of transversal)
⇒ 90° + ∠S = 180°
⇒ ∠S = 180° – 90° = 90°
Thus, ∠P = 50° and ∠S = 90°
Yes, there are more than one method to find m∠P.
PQRS is a quadrilateral. Sum of measures of all angles is 360°.
Since, we know the measurement of ∠Q, ∠R and ∠S.
∠Q = 130°, ∠R = 90° and ∠S = 90°
∠P + 130° + 90° + 90° = 360°
⇒ ∠P + 310° = 360°
⇒ ∠P = 360° – 310° = 50°
Exercise 3.4
1. State whether True or False.
(a) All rectangles are squares.
(b) All rhombuses are parallelograms.
(c) All squares are rhombuses and also rectangles.
(d) All squares are not parallelograms.
(e) All kites are rhombuses.
(f) All rhombuses are kites.
(g) All parallelograms are trapeziums.
(h) All squares are trapeziums.
Solution:
(a) False.
Because, all square are rectangles but all rectangles are not square.
(b) True
(c) True
(d) False.
Because, all squares are parallelograms as opposite sides are parallel and opposite angles are equal.
(e) False.
Because, for example, a length of the sides of a kite are not of same length.
(f) True
(g) True
(h) True
2. Identify all the quadrilaterals that have.
(a) four sides of equal length (b) four right angles
Solution:
(a) Rhombus and square have all four sides of equal length.
(b) Square and rectangle have four right angles.
3. Explain how a square is.
(i) a quadrilateral (ii) a parallelogram (iii) a rhombus (iv) a rectangle Solution
(i) Square is a quadrilateral because it has four sides.
(ii) Square is a parallelogram because it’s opposite sides are parallel and opposite angles are equal.
(iii) Square is a rhombus because all the four sides are of equal length and diagonals bisect at right angles.
(iv)Square is a rectangle because each interior angle, of the square, is 90°
4. Name the quadrilaterals whose diagonals.
(i) bisect each other (ii) are perpendicular bisectors of each other (iii) are equal Solution
(i) Parallelogram, Rhombus, Square and Rectangle
(ii) Rhombus and Square
(iii)Rectangle and Square
5. Explain why a rectangle is a convex quadrilateral. Solution
Rectangle is a convex quadrilateral because both of its diagonals lie inside the rectangle.
6. ABC is a right-angled triangle and O is the mid-point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you).
Solution
AD and DC are drawn so that AD || BC and AB || DC
AD = BC and AB = DC
ABCD is a rectangle as opposite sides are equal and parallel to each other and all the
interior angles are of 90°.
In a rectangle, diagonals are of equal length and also bisects each other.
Hence, AO = OC = BO = OD
Thus, O is equidistant from A, B and C.


