Algebra is a branch of mathematics that deals with variables and constants and the operations that can be performed on them. One of the foundational concepts in algebra is the use of algebraic identities. These identities provide a way to simplify and solve complex algebraic expressions quickly and efficiently.
An algebraic identity is an equation that holds true for all values of the variables involved. These identities are useful for simplifying expressions, expanding binomials, and solving equations. Essentially, they are shortcuts that save time when solving algebraic problems.

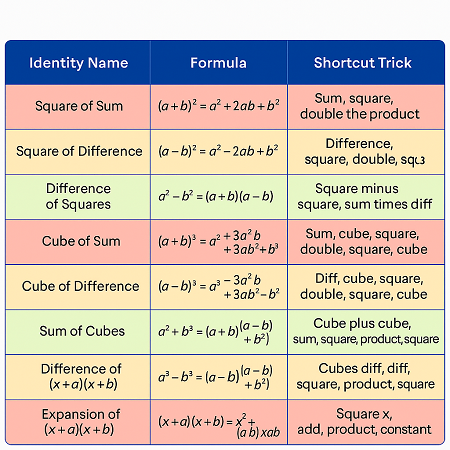
Common Algebraic Identities
- Square of Sum — (a+b)2 = a2+2ab+b2
Trick:
👉 Square first, double the product, square second.
(Think: “square-double-square”)
- Square of Difference — (a−b)2 = a2−2ab+b2
Trick:
👉 Square first, double the product (with minus), square second.
(Think: “square-minus-double-square”)
- Difference of Squares — a2−b2 = (a+b)(a−b)
Trick:
👉 Square minus square equals (sum)(difference).
(Think: “a big shortcut for factoring”)
- Cube of Sum — (a+b)3 = a3+3a2b+3ab2+b3
Trick:
👉 Cube first, square then multiply × 3, again multiply × 3 with squared second, cube second.
(Think: “cube-square-double-square-cube”)
- Cube of Difference — (a−b)3 = a3−3a2b+3ab2−b3
Trick:
👉 Same as cube of sum but alternate signs (+, –, +, –).
- Sum of Cubes — a3+b3 = (a+b)(a2−ab+b2
Trick:
👉 First sign same, second sign opposite, third sign always plus.
(Think: “plus-minus-plus”)
- Difference of Cubes — a3−b3 = (a−b)(a2+ab+b2
Trick:
👉 First sign same, second sign opposite, third sign always plus.
(Think: “minus-plus-plus”)
- Expansion of — (x+a)(x+b) = x2+(a+b)x+ab
Trick:
👉 x squared, sum of numbers × x, product of numbers.
(Think: “square-sum-product”)
Important Algebra Formulas