NCERT Solutions Ch-10 Circles
Chapter 10 of NCERT Class 9 Maths focuses on circles, covering essential concepts and theorems related to them. It begins with defining a circle as the set of all points in a plane that are equidistant from a fixed point known as the center. Key terms such as radius, diameter, chord, and circumference are introduced, along with their relationships. The chapter also explores the properties of tangents, including the tangent to a circle being perpendicular to the radius at the point of contact. Important theorems, such as the fact that the lengths of tangents drawn from an external point to a circle are equal, are discussed with proofs and examples.
NCERT Solutions of Class 9th Chapter 10 Circles Exercise 10.1, 10.2, 10.3, 10.4, 10.5
We try to teach you all Questions in easy way. We solve all chapter wise sums of maths textbook. In every chapter include NCERT solutions. For solutions of Exercise 10.1, 10.2, 10.3, 10.4, 10.5 click on Tabs :
1. Fill in the blanks:
(i) The centre of a circle lies in ____________ of the circle. (exterior/ interior)
(ii) A point, whose distance from the centre of a circle is greater than its radius lies in __________ of the circle. (exterior/ interior)
(iii) The longest chord of a circle is a _____________ of the circle.
(iv) An arc is a ___________ when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and _____________ of the circle.
(vi) A circle divides the plane, on which it lies, in _____________ parts.
Solution:
(i) The centre of a circle lies in interior of the circle.
(ii) A point, whose distance from the centre of a circle is greater than its radius lies in exterior of the circle.
(iii) The longest chord of a circle is a diameter of the circle.
(iv) An arc is a semicircle when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and chord of the circle.
(vi) A circle divides the plane, on which it lies, in 3 (three) parts.
2. Write True or False: Give reasons for your Solutions.
(i) Line segment joining the centre to any point on the circle is a radius of the circle.
(ii) A circle has only finite number of equal chords.
(iii) If a circle is divided into three equal arcs, each is a major arc.
(iv) A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
(v) Sector is the region between the chord and its corresponding arc.
(vi) A circle is a plane figure.
Solution:
(i) True. Any line segment drawn from the centre of the circle to any point on it is the radius of the circle and will be of equal length.
(ii) False. There can be infinite numbers of equal chords of a circle.
(iii) False. For unequal arcs, there can be major and minor arcs. So, equal arcs on a circle cannot be said as a major arc or a minor arc.
(iv) True. Any chord whose length is twice as long as the radius of the circle always passes through the centre of the circle and thus, it is known as the diameter of the circle.
(v) False. A sector is a region of a circle between the arc and the two radii of the circle.
(vi) True. A circle is a 2d figure and it can be drawn on a plane.
- Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
Solution:
To recall, a circle is a collection of points whose every point is equidistant from its centre. So, two circles can be congruent only when the distance of every point of both the circles are equal from the centre.
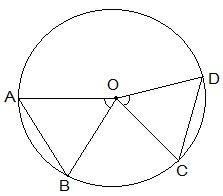
For the second part of the question, it is given that AB = CD i.e. two equal chords.
Now, it is to be proven that angle AOB is equal to angle COD.
Proof:
Consider the triangles ΔAOB and ΔCOD,
OA = OC and OB = OD (Since they are the radii of the circle)
AB = CD (As given in the question)
So, by SSS congruency, ΔAOB ΔCOD
∴ By CPCT we have,
AOB = COD. (Hence proved).
2. Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Solution:

Here, it is given that AOB = COD i.e. they are equal angles.
Now, we will have to prove that the line segments AB and CD are equal i.e. AB = CD.
Proof:
In triangles AOB and COD,
AOB = COD (as given in the question)
OA = OC and OB = OD (these are the radii of the circle)
So, by SAS congruency, ΔAOB ΔCOD.
∴ By the rule of CPCT, we have
AB = CD. (Hence proved).
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Solution:
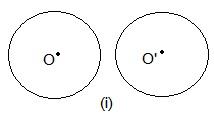
In these two circles, no point is common.

Here, only one point “P” is common.
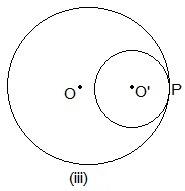
Even here, P is the common point.
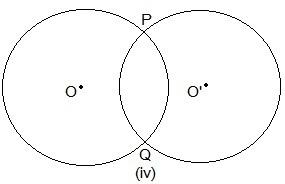
Here, two points are common which are P and Q.
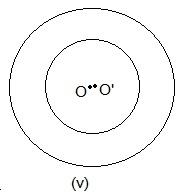
No point is common in the above circle.
2. Suppose you are given a circle. Give a construction to find its centre.
Solution:
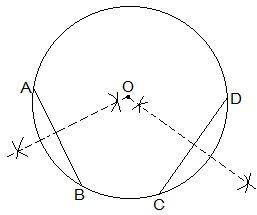
The construction steps to find the center of the circle are:
Step I: Draw a circle first.
Step II: Draw 2 chords AB and CD in the circle.
Step III: Draw the perpendicular bisectors of AB and CD.
Step IV: Connect the two perpendicular bisectors at a point. This intersection point of the two perpendicular bisectors is the centre of the circle.
3. If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Solution:
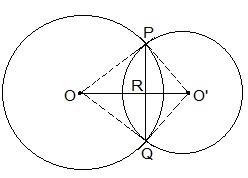
It is given that two circles intersect each other at P and Q.
To prove:
OO’ is perpendicular bisector of PQ.
Proof:
Triangle ΔPOO’ and ΔQOO’ are similar by SSS congruency since
OP = OQ and O’P = OQ (Since they are also the radii)
OO’ = OO’ (It is the common side)
So, It can be said that ΔPOO’ ΔQOO’
∴ POO’ = QOO’ — (i)
Even triangles ΔPOR and ΔQOR are similar by SAS congruency as
OP = OQ (Radii)
POR = QOR (As POO’ = QOO’)
OR = OR (Common arm)
So, ΔPOR ΔQOR
∴ PRO = QRO
Also, we know that
PRO+QRO = 180°
Hence, PRO = QRO = 180°/2 = 90°
So, OO’ is the perpendicular bisector of PQ.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Solution:
Given parameters are:
OP = 5cm
OS = 4cm and
PS = 3cm
Also, PQ = 2PR
Now, suppose RS = x. The diagram for the same is shown below.
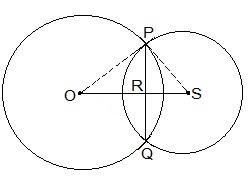
Consider the ΔPOR,
OP2 = OR2+PR2
⇒ 52 = (4-x)2+PR2
⇒ 25 = 16+x2-8x+PR2
∴ PR2 = 9-x2+8x — (i)
Now consider ΔPRS,
PS2 = PR2+RS2
⇒ 32 = PR2+x2
∴ PR2 = 9-x2 — (ii)
By equating equation (i) and equation (ii) we get,
9 -x2+8x = 9-x2
⇒ 8x = 0
⇒ x = 0
Now, put the value of x in equation (i)
PR2 = 9-02
⇒ PR = 3cm
∴ The length of the cord i.e. PQ = 2PR
So, PQ = 2×3 = 6cm
2. If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Solution:
Let AB and CD be two equal cords (i.e. AB = CD). In the above question, it is given that AB and CD intersect at a point, say, E.
It is now to be proven that the line segments AE = DE and CE = BE
Construction Steps:
Step 1: From the center of the circle, draw a perpendicular to AB i.e. OM ⊥ AB
Step 2: Similarly, draw ON ⊥ CD.
Step 3: Join OE.
Now, the diagram is as follows-
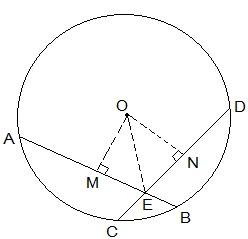
Proof:
From the diagram, it is seen that OM bisects AB and so, OM ⊥ AB
Similarly, ON bisects CD and so, ON ⊥ CD
It is known that AB = CD. So,
AM = ND — (i)
and MB = CN — (ii)
Now, triangles ΔOME and ΔONE are similar by RHS congruency since
OME = ONE (They are perpendiculars)
OE = OE (It is the common side)
OM = ON (AB and CD are equal and so, they are equidistant from the centre)
∴ ΔOME ΔONE
ME = EN (by CPCT) — (iii)
Now, from equations (i) and (ii) we get,
AM+ME = ND+EN
So, AE = ED
Now from equations (ii) and (iii) we get,
MB-ME = CN-EN
So, EB = CE (Hence proved).
3. If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Solution:
From the question we know the following:
(i) AB and CD are 2 chords which are intersecting at point E.
(ii) PQ is the diameter of the circle.
(iii) AB = CD.
Now, we will have to prove that BEQ = CEQ
For this, the following construction has to be done:
Construction:
Draw two perpendiculars are drawn as OM ⊥ AB and ON ⊥ D. Now, join OE. The constructed diagram will look as follows:
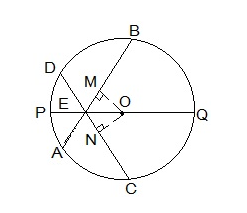
Now, consider the triangles ΔOEM and ΔOEN.
Here,
(i) OM = ON [Since the equal chords are always equidistant from the centre]
(ii) OE = OE [It is the common side]
(iii) OME = ONE [These are the perpendiculars]
So, by RHS congruency criterion, ΔOEM ΔOEN.
Hence, by CPCT rule, MEO = NEO
∴ BEQ = CEQ (Hence proved).
4. If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD (see Fig. 10.25).
Solution:
The given image is as follows:
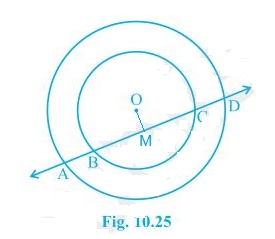
First, draw a line segment from O to AD such that OM ⊥ AD.
So, now OM is bisecting AD since OM ⊥ AD.
Therefore, AM = MD — (i)
Also, since OM ⊥ BC, OM bisects BC.
Therefore, BM = MC — (ii)
From equation (i) and equation (ii),
AM-BM = MD-MC
∴ AB = CD
5. Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6m each, what is the distance between Reshma and Mandip?
Solution:
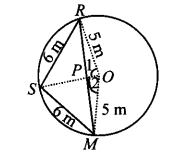
Equal chords of a circle subtend equal angles at the centre.
∴ ∠1 = ∠2
In ∆POR and ∆POM, we have
OP = OP [Common]
OR = OM [Radii of the same circle]
∠1 = ∠2 [Proved above]
∴ ∆POR ≅ ∆POM [By SAS congruence criteria]
∴ PR = PM and
∠OPR = ∠OPM [C.P.C.T.]
∵∠OPR + ∠OPM = 180° [Linear pair]
∴∠OPR = ∠OPM = 90°
⇒ OP ⊥ RM
Now, in ∆RSP and ∆MSP, we have
RS = MS [Each 6 cm]
SP = SP [Common]
PR = PM [Proved above]
∴ ∆RSP ≅ ∆MSP [By SSS congruence criteria]
⇒ ∠RPS = ∠MPS [C.P.C.T.]
But ∠RPS + ∠MPS = 180° [Linear pair]
⇒ ∠RPS = ∠MPS = 90°
SP passes through O.
Let OP = x m
∴ SP = (5 – x)m
Now, in right ∆OPR, we have
x2 + RP2 = 52
RP2 = 52 – x2
In right ∆SPR, we have
(5 – x)2 + RP2 = 62
⇒ RP2 = 62 – (5 – x)2 ……..(ii)
From (i) and (ii), we get
⇒ 52 – x2 = 62 – (5 – x)2
⇒ 25 – x2 = 36 – [25 – 10x + x2]
⇒ – 10x + 14 = 0
⇒ 10x = 14 ⇒ x =14/10 = 1.4
Now, RP2 = 52 – x2
⇒ RP2 = 25 – (1.4)2
⇒ RP2 = 25 – 1.96 = 23.04
∴ RP = 4.8
∴ RM = 2RP = 2 x 4.8 = 9.6
Thus, distance between Reshma and Mandip is 9.6 m.
6. A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
Solution:
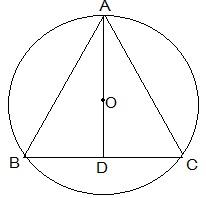
Here the positions of Ankur, Syed and David are represented as A, B and C respectively. Since they are sitting at equal distances, the triangle ABC will form an equilateral triangle.
AD ⊥ BC is drawn. Now, AD is median of ΔABC and it passes through the centre O.
Also, O is the centroid of the ΔABC. OA is the radius of the triangle.
OA = 2/3 AD
Let the side of a triangle a metres then BD = a/2 m.
Applying Pythagoras theorem in ΔABD,
AB2 = BD2+AD2
⇒ AD2 = AB2 -BD2
⇒ AD2 = a2 -(a/2)2
⇒ AD2 = 3a2/4
⇒ AD = √3a/2
OA = 2/3 AD
20 m = 2/3 × √3a/2
a = 20√3 m
So, the length of the string of the toy is 20√3 m.
In Fig. 10.36, A,B and C are three points on a circle with centre O such that BOC = 30° and AOB = 60°. If D is a point on the circle other than the arc ABC, find ADC.
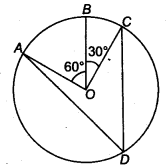
Solution:
It is given that,
AOC = AOB+BOC
So, AOC = 60°+30°
∴ AOC = 90°
It is known that an angle which is subtended by an arc at the centre of the circle is double the angle subtended by that arc at any point on the remaining part of the circle.
So,
ADC = (½)AOC
= (½)× 90° = 45°
2. A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Solution:
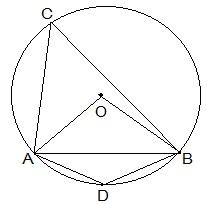
Here, the chord AB is equal to the radius of the circle. In the above diagram, OA and OB are the two radii of the circle.
Now, consider the ΔOAB. Here,
AB = OA = OB = radius of the circle.
So, it can be said that ΔOAB has all equal sides and thus, it is an equilateral triangle.
∴ AOC = 60°
And, ACB = ½ AOB
So, ACB = ½ × 60° = 30°
Now, since ACBD is a cyclic quadrilateral,
ADB +ACB = 180° (Since they are the opposite angles of a cyclic quadrilateral)
So, ADB = 180°-30° = 150°
So, the angle subtended by the chord at a point on the minor arc and also at a point on the major arc are 150° and 30° respectively.
3. In Fig. 10.37, PQR = 100°, where P, Q and R are points on a circle with centre O. Find OPR.
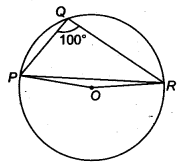
Solution:
Since angle which is subtended by an arc at the centre of the circle is double the angle subtended by that arc at any point on the remaining part of the circle.
So, the reflex POR = 2×PQR
We know the values of angle PQR as 100°
So, POR = 2×100° = 200°
∴ POR = 360°-200° = 160°
Now, in ΔOPR,
OP and OR are the radii of the circle
So, OP = OR
Also, OPR = ORP
Now, we know sum of the angles in a triangle is equal to 180 degrees
So,
POR+OPR+ORP = 180°
OPR+OPR = 180°-160°
As OPR = ORP
2OPR = 20°
Thus, OPR = 10°
4. In Fig. 10.38, ABC = 69°, ACB = 31°, find BDC.
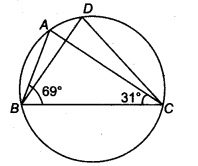
Solution:
We know that angles in the segment of the circle are equal so,
BAC = BDC
Now in the in ΔABC, sum of all the interior angles will be 180°
So, ABC+BAC+ACB = 180°
Now, by putting the values,
BAC = 180°-69°-31°
So, BAC = 80°
5. In Fig. 10.39, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠ BEC = 130° and ∠ ECD = 20°. Find BAC.
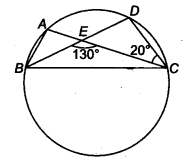
Solution:
We know that the angles in the segment of the circle are equal.
So,
∠ BAC = ∠ CDE
Now, by using the exterior angles property of the triangle In ΔCDE we get,
∠ CEB = ∠ CDE+∠ DCE
We know that ∠ DCE is equal to 20°
So, ∠ CDE = 110°
∠ BAC and ∠ CDE are equal
∴ ∠ BAC = 110°
6. ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠ DBC = 70°, ∠ BAC is 30°, find ∠ BCD. Further, if AB = BC, find ∠ ECD.
Solution:
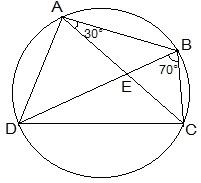
Consider the chord CD,
We know that angles in the same segment are equal.
So, ∠ CBD = ∠ CAD
∴ ∠ CAD = 70°
Now, ∠ BAD will be equal to the sum of angles BAC and CAD.
So, ∠ BAD = ∠ BAC+∠ CAD
= 30°+70°
∴ ∠ BAD = 100°
We know that the opposite angles of a cyclic quadrilateral sums up to 180 degrees.
So,
∠ BCD+∠ BAD = 180°
It is known that ∠ BAD = 100°
So, ∠ BCD = 80°
Now consider the ΔABC.
Here, it is given that AB = BC
Also, ∠ BCA = ∠ CAB (They are the angles opposite to equal sides of a triangle)
∠ BCA = 30°
also, ∠ BCD = 80°
∠ BCA +∠ ACD = 80°
Thus, ∠ ACD = 50° and ∠ ECD = 50°
7. If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
Solution:
Draw a cyclic quadrilateral ABCD inside a circle with center O such that its diagonal AC and BD are two diameters of the circle.
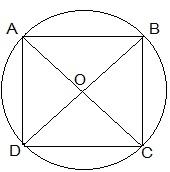
We know that the angles in the semi-circle are equal.
So, ∠ ABC = ∠ BCD = ∠ CDA = ∠ DAB = 90°
So, as each internal angle is 90°, it can be said that the quadrilateral ABCD is a rectangle.
8. If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Solution:
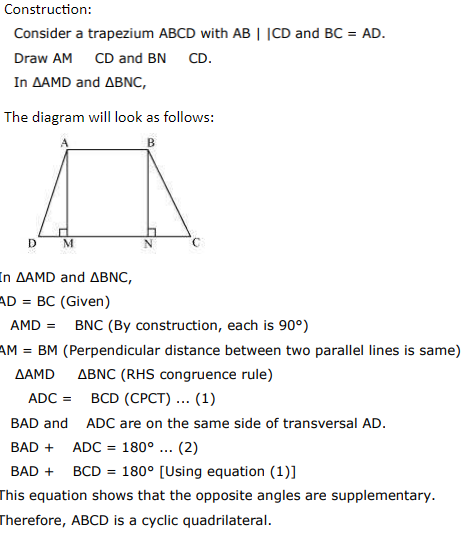
9. Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig. 10.40). Prove that ∠ ACP = ∠ QCD.
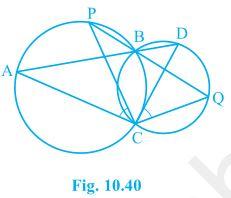
Construction:
Join the chords AP and DQ.
For chord AP, we know that angles in the same segment are equal.
So, ∠ PBA = ∠ ACP — (i)
Similarly for chord DQ,
∠ DBQ = ∠ QCD — (ii)
It is known that ABD and PBQ are two line segments which are intersecting at B.
At B, the vertically opposite angles will be equal.
∴ ∠ PBA = ∠ DBQ — (iii)
From equation (i), equation (ii) and equation (iii) we get,
∠ ACP = ∠ QCD
10. If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Solution:
First draw a triangle ABC and then two circles having diameter as AB and AC respectively.
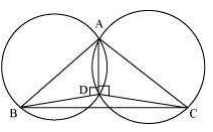
Proof:
We know that angle in the semi-circle are equal
So, ∠ ADB = ∠ ADC = 90°
Hence, ∠ ADB+∠ ADC = 180°
∴ ∠ BDC is straight line.
So, it can be said that D lies on the line BC.
11. ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠ CAD = ∠CBD.
Solution:
We know that AC is the common hypotenuse and ∠ B = ∠ D = 90°.
Now, it has to be proven that ∠ CAD = ∠ CBD
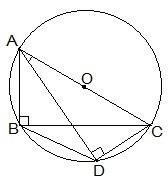
Since, ∠ ABC and ∠ ADC are 90°, it can be said that They lie in the semi-circle.
So, triangles ABC and ADC are in the semi-circle and the points A, B, C and D are concyclic.
Hence, CD is the chord of the circle with center O.
We know that the angles which are in the same segment of the circle are equal.
∴ ∠ CAD = ∠ CBD
12. Prove that a cyclic parallelogram is a rectangle.
Solution:
It is given that ABCD is a cyclic parallelogram and we will have to prove that ABCD is a rectangle.
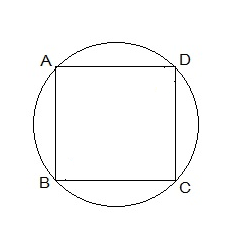
∴ Sum of its opposite angles is 180°.
⇒ ∠A + ∠C = 180° …(i)
But ∠A = ∠C …(ii)
[Opposite angles of a parallelogram are equal]
From (i) and (ii), we have
∠A = ∠C = 90°
Similarly,
∠B = ∠D = 90°
⇒ Each angle of the parallelogram ABCD is 90°.
Thus, ABCD is a rectangle.
