NCERT Solutions Ch-6 Triangles
Chapter 6 of the NCERT Maths book for Class 10, titled “Triangles,” dives into the fundamental concepts and properties of triangles, focusing on the similarity of triangles and various related theorems. This chapter introduces the concept of similarity in triangles, where students learn about similar figures and the criteria for triangle similarity, including the AA (Angle-Angle), SAS (Side-Angle-Side), and SSS (Side-Side-Side) criteria. Key theorems, such as the Basic Proportionality Theorem (also known as Thales’ theorem), play a significant role in understanding the relationship between sides of similar triangles. Additionally, the chapter covers the Pythagorean theorem and its applications in proving triangle similarity. These topics are presented through explanations, examples, and practice questions, allowing students to develop a solid foundation in triangle properties and problem-solving techniques.
NCERT Solutions Ch-6 Triangles Exercise 6.1, 6.2, 6.3 , 6.4 , 6.5 and 6.6
We try to teach you all Questions in easy way. We solve all chapter wise sums of maths textbook. In every chapter include NCERT solutions. For solutions of Exercise 6.1, 6.2, 6.3 , 6.4 , 6.5 and 6.6 click on Tabs :
Q1. Fill in the blanks using correct word given in the brackets:-
(i) All circles are __________. (congruent, similar)
Answer: Similar
(ii) All squares are __________. (similar, congruent)
Answer: Similar
(iii) All __________ triangles are similar. (isosceles, equilateral)
Answer: Equilateral
(iv) Two polygons of the same number of sides are similar, if (a) their corresponding angles are __________ and (b) their corresponding sides are __________. (equal, proportional)
Answer: (a) Equal
(b) Proportional
Q2. Give two different examples of pair of
(i) Similar figures
(ii) Non-similar figures
Solution:
(i) Similar figures :- A pair of equilateral triangles of different side lengths, A pair of two rectangles of differnt lengths and breadths, etc.
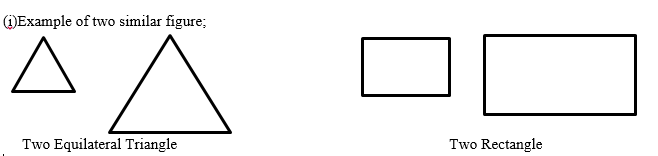
(ii) Non-similar figures :- A pair of Triangle and Rhombus with angles not equal to 90
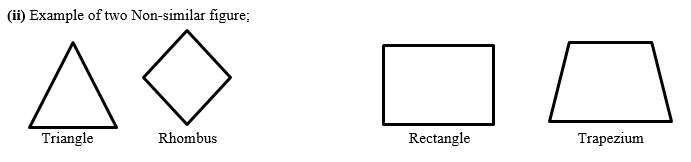
Q3. State whether the following quadrilaterals are similar or not:
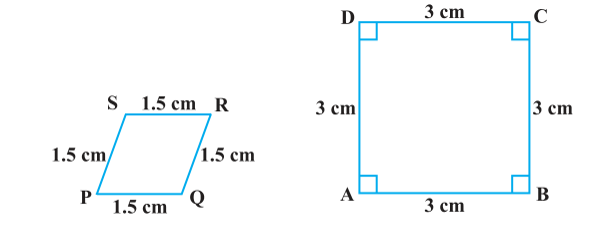
Solution: From the given two figures, we can see their corresponding angles are different or unequal. Therefore they are not similar.
Q1. In the given figure (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).
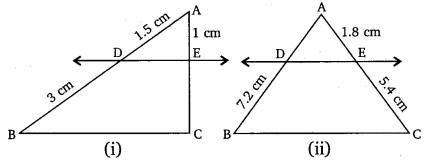
Solution:
(i) Given, in △ ABC, DE∥BC
∴ AD/DB = AE/EC [Using Basic proportionality theorem]
⇒1.5/3 = 1/EC
⇒EC = 3/1.5
EC = 3×10/15 = 2 cm
Hence, EC = 2 cm.
(ii) Given, in △ ABC, DE∥BC
∴ AD/DB = AE/EC [Using Basic proportionality theorem]
⇒ AD/7.2 = 1.8 / 5.4
⇒ AD = 1.8 ×7.2/5.4 = (18/10)×(72/10)×(10/54) = 24/10
⇒ AD = 2.4
Hence, AD = 2.4 cm.
Q2. E and F are points on the sides PQ and PR respectively of a ΔPQR. For each of the following cases, state whether EF || QR.
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.63 cm
Solution:
Given, in ΔPQR, E and F are two points on side PQ and PR respectively. See the figure below;
(i) Given, PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2,4 cm
Therefore, by using Basic proportionality theorem, we get,
PE/EQ = 3.9/3 = 39/30 = 13/10 = 1.3
And PF/FR = 3.6/2.4 = 36/24 = 3/2 = 1.5
So, we get, PE/EQ ≠ PF/FR
Hence, EF is not parallel to QR.
(ii) Given, PE = 4 cm, QE = 4.5 cm, PF = 8cm and RF = 9cm
Therefore, by using Basic proportionality theorem, we get,
PE/QE = 4/4.5 = 40/45 = 8/9
And, PF/RF = 8/9
So, we get here,
PE/QE = PF/RF
Hence, EF is parallel to QR.
(iii) Given, PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
From the figure,
EQ = PQ – PE = 1.28 – 0.18 = 1.10 cm
And, FR = PR – PF = 2.56 – 0.36 = 2.20 cm
So, PE/EQ = 0.18/1.10 = 18/110 = 9/55………….(i)
And, PE/FR = 0.36/2.20 = 36/220 = 9/55…………(ii)
So, we get here,
PE/EQ = PF/FR
Hence, EF is parallel to QR.
Q3. In the figure, if LM || CB and L
N || CD, prove that AM/AB = AN/AD
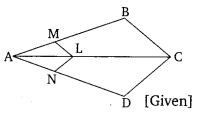
Solution:
In the given figure, we can see, LM || CB,
By using basic proportionality theorem, we get,
AM/AB = AL/LC…………………….. (i)
Similarly, given, LN || CD and using basic proportionality theorem,
∴AN/AD = AL/LC……………………………(ii)
From equation (i) and (ii), we get,
AM/AB = AN/AD
Hence, proved.
Q4. In the figure, DE||AC and DF||AE. Prove that BF/FE = BE/EC
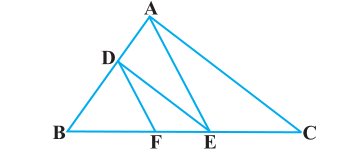
Solution:
In ΔABC, given as, DE || AC
Thus, by using Basic Proportionality Theorem, we get,
∴BD/DA = BE/EC ………………………………………………(i)
In ΔABC, given as, DF || AE
Thus, by using Basic Proportionality Theorem, we get,
∴BD/DA = BF/FE ………………………………………………(ii)
From equation (i) and (ii), we get
BE/EC = BF/FE
Hence, proved.
Q5. In the figure, DE||OQ and DF||OR, show that EF||QR.
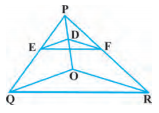
Solution:
Given,
In ΔPQO, DE || OQ
So by using Basic Proportionality Theorem,
PD/DO = PE/EQ ………………. (i)
Again given, in ΔPQO, DE || OQ ,
So by using Basic Proportionality Theorem,
PD/DO = PF/FR ………………… (ii)
From equation (i) and (ii), we get,
PE/EQ = PF/FR
Therefore, by converse of Basic Proportionality Theorem,
EF || QR, in ΔPQR.
6. In the figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
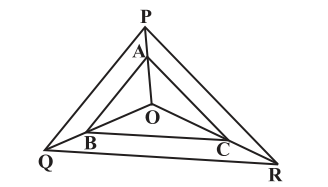
Solution:
Given here,
In ΔOPQ, AB || PQ
By using Basic Proportionality Theorem,
OA/AP = OB/BQ…………….(i)
Also given,
In ΔOPR, AC || PR
By using Basic Proportionality Theorem
∴ OA/AP = OC/CR……………(ii)
From equation (i) and (ii), we get,
OB/BQ = OC/CR
Therefore, by converse of Basic Proportionality Theorem,
In ΔOQR, BC || QR.
Q7. Using Basic proportionality theorem, prove that a line drawn through the mid-points of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).
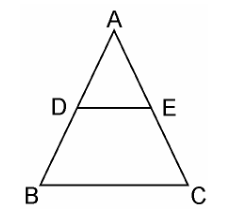
Solution:
Given, in ΔABC, D is the midpoint of AB such that AD=DB.
A line parallel to BC intersects AC at E as shown in above figure such that DE || BC.
We have to prove that E is the mid point of AC.
Since, D is the mid-point of AB.
∴ AD=DB
⇒AD/DB = 1 …………………………. (i)
In ΔABC, DE || BC,
By using Basic Proportionality Theorem,
Therefore, AD/DB = AE/EC
From equation (i), we can write,
⇒ 1 = AE/EC
∴ AE = EC
Hence, proved, E is the midpoint of AC.
8. Using Converse of basic proportionality theorem, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).
Solution:
Given, in ΔABC, D and E are the mid points of AB and AC respectively, such that,
AD=BD and AE=EC.

We have to prove that: DE || BC.
Since, D is the midpoint of AB
∴ AD=DB
⇒AD/BD = 1……………………………….. (i)
Also given, E is the mid-point of AC.
∴ AE=EC
⇒ AE/EC = 1
From equation (i) and (ii), we get,
AD/BD = AE/EC
By converse of Basic Proportionality Theorem,
DE || BC
Hence, proved.
9. ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that AO/BO = CO/DO.
Solution:
Given, ABCD is a trapezium where AB || DC and diagonals AC and BD intersect each other at O.
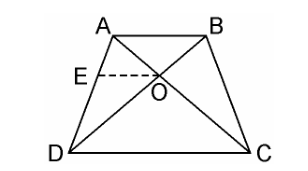
We have to prove, AO/BO = CO/DO
From the point O, draw a line EO touching AD at E, in such a way that,
EO || DC || AB
In ΔADC, we have OE || DC
Therefore, By using Basic Proportionality Theorem
AE/ED = AO/CO ……………..(i)
Now, In ΔABD, OE || AB
Therefore, By using Basic Proportionality Theorem
DE/EA = DO/BO…………….(ii)
From equation (i) and (ii), we get,
AO/CO = BO/DO
⇒AO/BO = CO/DO
Hence, proved.
10. The diagonals of a quadrilateral ABCD intersect each other at the point O such that AO/BO = CO/DO. Show that ABCD is a trapezium.
Solution:
Given, Quadrilateral ABCD where AC and BD intersects each other at O such that,
AO/BO = CO/DO.

We have to prove here, ABCD is a trapezium
From the point O, draw a line EO touching AD at E, in such a way that,
EO || DC || AB
In ΔDAB, EO || AB
Therefore, By using Basic Proportionality Theorem
DE/EA = DO/OB ……………………(i)
Also, given,
AO/BO = CO/DO
⇒ AO/CO = BO/DO
⇒ CO/AO = DO/BO
⇒DO/OB = CO/AO …………………………..(ii)
From equation (i) and (ii), we get
DE/EA = CO/AO
Therefore, By using converse of Basic Proportionality Theorem,
EO || DC also EO || AB
⇒ AB || DC.
Hence, quadrilateral ABCD is a trapezium with AB || CD.
1. State which pairs of triangles in Figure, are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
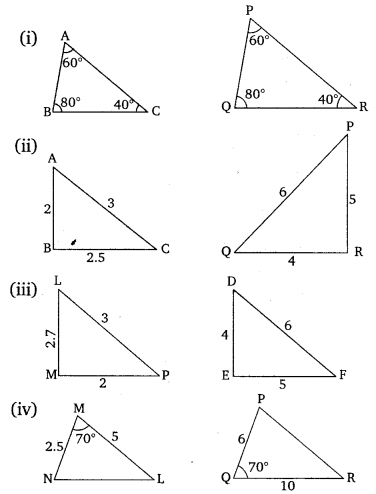
Solution:
(i) Given, in ΔABC and ΔPQR,
∠A = ∠P = 60°
∠B = ∠Q = 80°
∠C = ∠R = 40°
Therefore by AAA similarity criterion,
∴ ΔABC ~ ΔPQR
(ii) Given, in ΔABC and ΔPQR,
AB/QR = BC/RP = CA/PQ
By SSS similarity criterion,
ΔABC ~ ΔQRP
(iii) Given, in ΔLMP and ΔDEF,
LM = 2.7, MP = 2, LP = 3, EF = 5, DE = 4, DF = 6
MP/DE = 2/4 = 1/2
PL/DF = 3/6 = 1/2
LM/EF = 2.7/5 = 27/50
Here , MP/DE = PL/DF ≠ LM/EF
Therefore, ΔLMP and ΔDEF are not similar.
(iv) In ΔMNL and ΔQPR, it is given,
MN/QP = ML/QR = 1/2
∠M = ∠Q = 70°
Therefore, by SAS similarity criterion
∴ ΔMNL ~ ΔQPR
(v) In ΔABC and ΔDEF, given that,
AB = 2.5, BC = 3, ∠A = 80°, EF = 6, DF = 5, ∠F = 80°
Here , AB/DF = 2.5/5 = 1/2
And, BC/EF = 3/6 = 1/2
⇒ ∠B ≠ ∠F
Hence, ΔABC and ΔDEF are not similar.
(vi) In ΔDEF, by sum of angles of triangles, we know that,
∠D + ∠E + ∠F = 180°
⇒ 70° + 80° + ∠F = 180°
⇒ ∠F = 180° – 70° – 80°
⇒ ∠F = 30°
Similarly, In ΔPQR,
∠P + ∠Q + ∠R = 180 (Sum of angles of Δ)
⇒ ∠P + 80° + 30° = 180°
⇒ ∠P = 180° – 80° -30°
⇒ ∠P = 70°
Now, comparing both the triangles, ΔDEF and ΔPQR, we have
∠D = ∠P = 70°
∠F = ∠Q = 80°
∠F = ∠R = 30°
Therefore, by AAA similarity criterion,
Hence, ΔDEF ~ ΔPQR
Q2. In the figure, ΔODC ∝ ¼ ΔOBA, ∠ BOC = 125° and ∠ CDO = 70°. Find ∠ DOC, ∠ DCO and ∠ OAB.
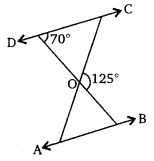
Solution:
As we can see from the figure, DOB is a straight line.
Therefore, ∠DOC + ∠ COB = 180°
⇒ ∠DOC = 180° – 125° (Given, ∠ BOC = 125°)
= 55°
In ΔDOC, Sum of the measures of the angles of a triangle is 180º
Therefore, ∠DCO + ∠ CDO + ∠ DOC = 180°
⇒ ∠DCO + 70º + 55º = 180°(Given, ∠ CDO = 70°)
⇒ ∠DCO = 55°
It is given that, ΔODC ∝ ¼ ΔOBA,
Therefore, ΔODC ~ ΔOBA.
Hence, Corresponding angles are equal in similar triangles
∠OAB = ∠OCD
⇒ ∠ OAB = 55°
∠OAB = ∠OCD
⇒ ∠OAB = 55°
Q3. Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that AO/OC = OB/OD
Solution:

In ΔDOC and ΔBOA,
AB || CD, thus alternate interior angles will be equal,
∴∠CDO = ∠ABO
Similarly,
∠DCO = ∠BAO
Also, for the two triangles ΔDOC and ΔBOA, vertically opposite angles will be equal;
∴∠DOC = ∠BOA
Hence, by AAA similarity criterion,
ΔDOC ~ ΔBOA
Thus, the corresponding sides are proportional.
DO/BO = OC/OA
⇒OA/OC = OB/OD
Hence, proved.
Q4. In the fig.6.36, QR/QS = QT/PR and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.
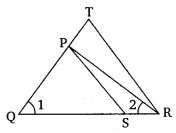
Solution:
In ΔPQR,
∠PQR = ∠PRQ
∴ PQ = PR ………………………(i)
Given,
QR/QS = QT/PRUsing equation (i), we get
QR/QS = QT/QP……………….(ii)
In ΔPQS and ΔTQR, by equation (ii),
QR/QS = QT/QP
∠Q = ∠Q
∴ ΔPQS ~ ΔTQR [By SAS similarity criterion]
Q5. S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ~ ΔRTS.
Solution:
Given, S and T are point on sides PR and QR of ΔPQR
And ∠P = ∠RTS.
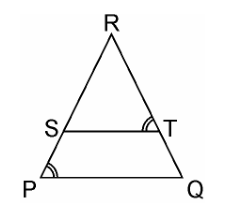
In ΔRPQ and ΔRTS,
∠RTS = ∠QPS (Given)
∠R = ∠R (Common angle)
∴ ΔRPQ ~ ΔRTS (AA similarity criterion)
Q6. In the figure, if ΔABE ≅ ΔACD, show that ΔADE ~ ΔABC.
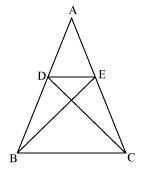
Solution:
Given, ΔABE ≅ ΔACD.
∴ AB = AC [By CPCT] ……………………………….(i)
And, AD = AE [By CPCT] ……………………………(ii)
In ΔADE and ΔABC, dividing eq.(ii) by eq(i),
AD/AB = AE/AC
∠A = ∠A [Common angle]
∴ ΔADE ~ ΔABC [SAS similarity criterion]
Q7. In the figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
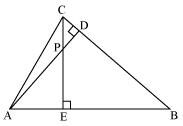
Solution:
Given, altitudes AD and CE of ΔABC intersect each other at the point P.
(i) In ΔAEP and ΔCDP,
∠AEP = ∠CDP (90° each)
∠APE = ∠CPD (Vertically opposite angles)
Hence, by AA similarity criterion,
ΔAEP ~ ΔCDP
(ii) In ΔABD and ΔCBE,
∠ADB = ∠CEB ( 90° each)
∠ABD = ∠CBE (Common Angles)
Hence, by AA similarity criterion,
ΔABD ~ ΔCBE
(iii) In ΔAEP and ΔADB,
∠AEP = ∠ADB (90° each)
∠PAE = ∠DAB (Common Angles)
Hence, by AA similarity criterion,
ΔAEP ~ ΔADB
(iv) In ΔPDC and ΔBEC,
∠PDC = ∠BEC (90° each)
∠PCD = ∠BCE (Common angles)
Hence, by AA similarity criterion,
ΔPDC ~ ΔBEC
Q8. E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ~ ΔCFB.
Solution:
Given, E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Consider the figure below,
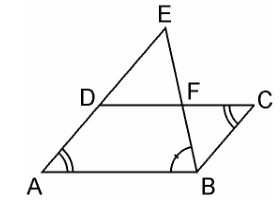
In ΔABE and ΔCFB,
∠A = ∠C (Opposite angles of a parallelogram)
∠AEB = ∠CBF (Alternate interior angles as AE || BC)
∴ ΔABE ~ ΔCFB (AA similarity criterion)
Q9. In the figure, ABC and AMP are two right triangles, right angled at B and M respectively, prove that:
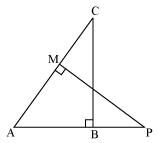
(i) ΔABC ~ ΔAMP
(ii) CA/PA = BC/MP
Solution:
Given, ABC and AMP are two right triangles, right angled at B and M respectively.
(i) In ΔABC and ΔAMP, we have,
∠CAB = ∠MAP (common angles)
∠ABC = ∠AMP = 90° (each 90°)
∴ ΔABC ~ ΔAMP (AA similarity criterion)
(ii) As, ΔABC ~ ΔAMP (AA similarity criterion)
If two triangles are similar then the corresponding sides are always equal,
Hence, CA/PA = BC/MP
Q10. CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC ~ ΔFEG, Show that:
(i) CD/GH = AC/FG
(ii) ΔDCB ~ ΔHGE
(iii) ΔDCA ~ ΔHGF
Solution: Given, CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively.
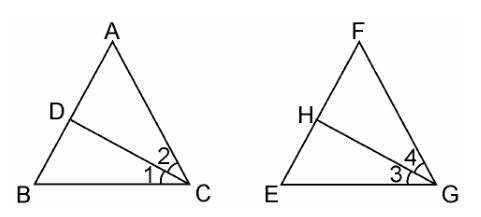
(i) From the given condition,
ΔABC ~ ΔFEG.
∴ ∠A = ∠F, ∠B = ∠E, and ∠ACB = ∠FGE
Since, ∠ACB = ∠FGE
∴ ∠ACD = ∠FGH (Angle bisector)
And, ∠DCB = ∠HGE (Angle bisector)
In ΔACD and ΔFGH,
∠A = ∠F
∠ACD = ∠FGH
∴ ΔACD ~ ΔFGH (AA similarity criterion)
⇒CD/GH = AC/FG
(ii) In ΔDCB and ΔHGE,
∠DCB = ∠HGE (Already proved)
∠B = ∠E (Already proved)
∴ ΔDCB ~ ΔHGE (AA similarity criterion)
(iii) In ΔDCA and ΔHGF,
∠ACD = ∠FGH (Already proved)
∠A = ∠F (Already proved)
∴ ΔDCA ~ ΔHGF (AA similarity criterion)
Q11. In the following figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ΔABD ~ ΔECF.
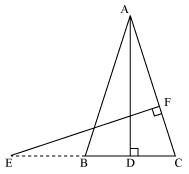
Solution: Given, ABC is an isosceles triangle.
∴ AB = AC
⇒ ∠ABD = ∠ECF
In ΔABD and ΔECF,
∠ADB = ∠EFC (Each 90°)
∠BAD = ∠CEF (Already proved)
∴ ΔABD ~ ΔECF (using AA similarity criterion)
12. Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR (see Fig 6.41). Show that ΔABC ~ ΔPQR.
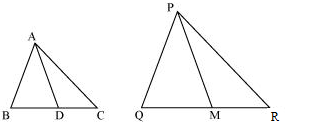
Solution: Given, ΔABC and ΔPQR, AB, BC and median AD of ΔABC are proportional to sides PQ, QR and median PM of ΔPQR
i.e. AB/PQ = BC/QR = AD/PM
We have to prove: ΔABC ~ ΔPQR
As we know here,
AB/PQ = BC/QR = AD/PM

⇒AB/PQ = BC/QR = AD/PM (D is the midpoint of BC. M is the midpoint of QR)
⇒ ΔABD ~ ΔPQM [SSS similarity criterion]
∴ ∠ABD = ∠PQM [Corresponding angles of two similar triangles are equal]
⇒ ∠ABC = ∠PQR
In ΔABC and ΔPQR
AB/PQ = BC/QR ………………………….(i)
∠ABC = ∠PQR ……………………………(ii)
From equation (i) and (ii), we get,
ΔABC ~ ΔPQR [SAS similarity criterion]
Q13. D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC. Show that CA2 = CB.CD
Solution: Given, D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC.
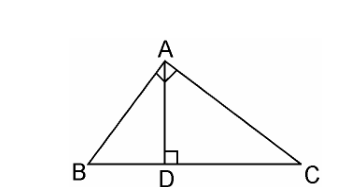
In ΔADC and ΔBAC,
∠ADC = ∠BAC (Already given)
∠ACD = ∠BCA (Common angles)
∴ ΔADC ~ ΔBAC (AA similarity criterion)
We know that corresponding sides of similar triangles are in proportion.
∴ CA/CB = CD/CA
⇒ CA2 = CB.CD.
Hence, proved.
Q14. Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
Solution: Given: Two triangles ΔABC and ΔPQR in which AD and PM are medians such that;
AB/PQ = AC/PR = AD/PM
We have to prove, ΔABC ~ ΔPQR
Let us construct first: Produce AD to E so that AD = DE. Join CE, Similarly produce PM to N such that PM = MN, also Join RN.
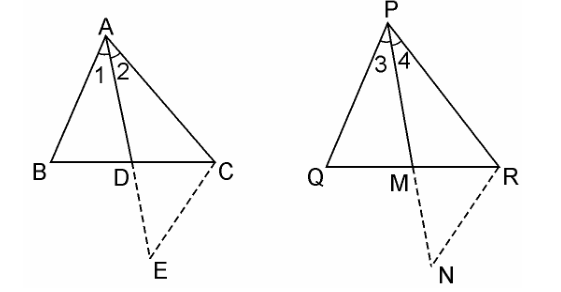
In ΔABD and ΔCDE, we have
AD = DE [By Construction.]
BD = DC [Since, AP is the median]
and, ∠ADB = ∠CDE [Vertically opposite angles]
∴ ΔABD ≅ ΔCDE [SAS criterion of congruence]
⇒ AB = CE [By CPCT] …………………………..(i)
Also, in ΔPQM and ΔMNR,
PM = MN [By Construction.]
QM = MR [Since, PM is the median]
and, ∠PMQ = ∠NMR [Vertically opposite angles]
∴ ΔPQM = ΔMNR [SAS criterion of congruence]
⇒ PQ = RN [CPCT] ………………………………(ii)
Now, AB/PQ = AC/PR = AD/PM
From equation (i) and (ii),
⇒CE/RN = AC/PR = AD/PM
⇒ CE/RN = AC/PR = 2AD/2PM
⇒ CE/RN = AC/PR = AE/PN [Since 2AD = AE and 2PM = PN]
∴ ΔACE ~ ΔPRN [SSS similarity criterion]
Therefore, ∠2 = ∠4
Similarly, ∠1 = ∠3
∴ ∠1 + ∠2 = ∠3 + ∠4
⇒ ∠A = ∠P …………………………………………….(iii)
Now, In ΔABC and ΔPQR, we have
AB/PQ = AC/PR (Already given)
From equation (iii),
∠A = ∠P
∴ ΔABC ~ ΔPQR [ SAS similarity criterion]
Q15. A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Solution:
Given, Length of the vertical pole = 6m
Shadow of the pole = 4 m
Let Height of tower = h m
Length of shadow of the tower = 28 m
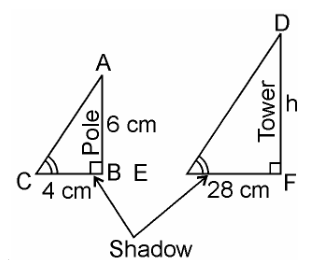
In ΔABC and ΔDEF,
∠C = ∠E (angular elevation of sum)
∠B = ∠F = 90°
∴ ΔABC ~ ΔDEF (AA similarity criterion)
∴ AB/DF = BC/EF (If two triangles are similar corresponding sides are proportional)
∴ 6/h = 4/28
⇒h =( 6×28)/4
⇒ h = 6 × 7
⇒ h = 42 m
Hence, the height of the tower is 42 m.
Q16. If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR prove that AB/PQ = AD/PM.
Solution: Given, ΔABC ~ ΔPQR
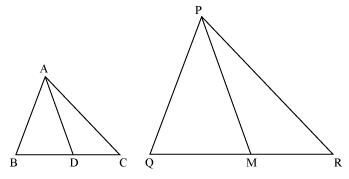
We know that the corresponding sides of similar triangles are in proportion.
∴AB/PQ = AC/PR = BC/QR……………………………(i)
Also, ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R ………….…..(ii)
Since AD and PM are medians, they will divide their opposite sides.
∴ BD = BC/2 and QM = QR/2 ……………..………….(iii)
From equations (i) and (iii), we get
AB/PQ = BD/QM ……………………….(iv)
In ΔABD and ΔPQM,
From equation (ii), we have
∠B = ∠Q
From equation (iv), we have,
AB/PQ = BD/QM
∴ ΔABD ~ ΔPQM (SAS similarity criterion)
⇒AB/PQ = BD/QM = AD/PM
Q1. Let ΔABC ~ ΔDEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC.
Solution: Given, ΔABC ~ ΔDEF,
Area of ΔABC = 64 cm2
Area of ΔDEF = 121 cm2
EF = 15.4 cm
As we know, if two triangles are similar, ratio of their areas are equal to the square of the ratio of their corresponding sides,
= AC2/DF2 = BC2/EF2
∴ 64/121 = BC2/EF2
⇒ (8/11)2 = (BC/15.4)2
⇒ 8/11 = BC/15.4
⇒ BC = 8×15.4/11
⇒ BC = 8 × 1.4
⇒ BC = 11.2 cm
Q2. Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2CD, find the ratio of the areas of triangles AOB and COD.
Solution: Given, ABCD is a trapezium with AB || DC. Diagonals AC and BD intersect each other at point O.
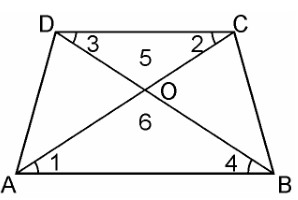
In ΔAOB and ΔCOD, we have
∠1 = ∠2 (Alternate angles)
∠3 = ∠4 (Alternate angles)
∠5 = ∠6 (Vertically opposite angle)
∴ ΔAOB ~ ΔCOD [AAA similarity criterion]
As we know, If two triangles are similar then the ratio of their areas are equal to the square of the ratio of their corresponding sides. Therefore,
Area of (ΔAOB)/Area of (ΔCOD) = AB2/CD2
= (2CD)2/CD2 [∴ AB = CD]
∴ Area of (ΔAOB)/Area of (ΔCOD)
= 4CD2/CD = 4/1
Hence, the required ratio of the area of ΔAOB and ΔCOD = 4:1
Q3. In the figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that area (ΔABC)/area (ΔDBC) = AO/DO.
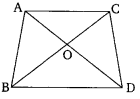
Q4. If the areas of two similar triangles are equal, prove that they are congruent.
Solution: Say ΔABC and ΔPQR are two similar triangles and equal in area
Now let us prove ΔABC ≅ ΔPQR.
Since, ΔABC ~ ΔPQR
∴ Area of (ΔABC)/Area of (ΔPQR) = BC2/QR2
⇒ BC2/QR2 =1 [Since, Area(ΔABC) = (ΔPQR)
⇒ BC2/QR2
⇒ BC = QR
Similarly, we can prove that
AB = PQ and AC = PR
Thus, ΔABC ≅ ΔPQR [SSS criterion of congruence]
5. D, E and F are respectively the mid-points of sides AB, BC and CA of ΔABC. Find the ratio of the area of ΔDEF and ΔABC.
Solution: Given, D, E and F are respectively the mid-points of sides AB, BC and CA of ΔABC.
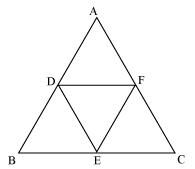
In ΔABC,
F is the mid point of AB (Already given)
E is the mid-point of AC (Already given)
So, by the mid-point theorem, we have,
FE || BC and FE = 1/2BC
⇒ FE || BC and FE || BD [BD = 1/2BC]
Since, opposite sides of parallelogram are equal and parallel
∴ BDEF is parallelogram.
Similarly in ΔFBD and ΔDEF, we have
FB = DE (Opposite sides of parallelogram BDEF)
FD = FD (Common sides)
BD = FE (Opposite sides of parallelogram BDEF)
∴ ΔFBD ≅ ΔDEF
Similarly, we can prove that
ΔAFE ≅ ΔDEF
ΔEDC ≅ ΔDEF
As we know, if triangles are congruent, then they are equal in area.
So,
Area(ΔFBD) = Area(ΔDEF) ……………………………(i)
Area(ΔAFE) = Area(ΔDEF) ……………………………….(ii)
and,
Area(ΔEDC) = Area(ΔDEF) ………………………….(iii)
Now,
Area(ΔABC) = Area(ΔFBD) + Area(ΔDEF) + Area(ΔAFE) + Area(ΔEDC) ………(iv)
Area(ΔABC) = Area(ΔDEF) + Area(ΔDEF) + Area(ΔDEF) + Area(ΔDEF)
From equation (i), (ii) and (iii),
⇒ Area(ΔDEF) = (1/4)Area(ΔABC)
⇒ Area(ΔDEF)/Area(ΔABC) = 1/4
Hence, Area(ΔDEF):Area(ΔABC) = 1:4
Q6. Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Solution: Given: AM and DN are the medians of triangles ABC and DEF respectively and ΔABC ~ ΔDEF.
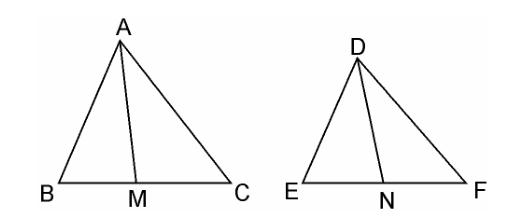
We have to prove: Area(ΔABC)/Area(ΔDEF) = AM2/DN2
Since, ΔABC ~ ΔDEF (Given)
∴ Area(ΔABC)/Area(ΔDEF) = (AB2/DE2) ……………………………(i)
and, AB/DE = BC/EF = CA/FD ………………………………………(ii)
In ΔABM and ΔDEN,
Since ΔABC ~ ΔDEF
∴ ∠B = ∠E
AB/DE = BM/EN [Already Proved in equation (i)]
∴ ΔABC ~ ΔDEF [SAS similarity criterion]
⇒ AB/DE = AM/DN …………………………………………………..(iii)
∴ ΔABM ~ ΔDEN
As the areas of two similar triangles are proportional to the squares of the corresponding sides.
∴ area(ΔABC)/area(ΔDEF) = AB2/DE2 = AM2/DN2
Q7. Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Solution: Given, ABCD is a square whose one diagonal is AC. ΔAPC and ΔBQC are two equilateral
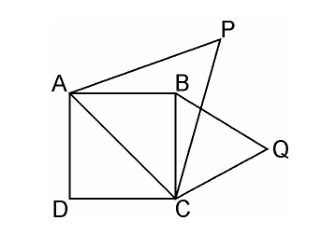
square ABCD.
Area(ΔBQC) = ½ Area(ΔAPC)
Since, ΔAPC and ΔBQC are both equilateral triangles, as per given,
∴ ΔAPC ~ ΔBQC [AAA similarity criterion]
∴ area(ΔAPC)/area(ΔBQC) = (AC2/BC2) = AC2/BC2
Since, Diagonal = √2 side = √2 BC
⇒ area(ΔAPC) = 2 × area(ΔBQC)
⇒ area(ΔBQC) = 1/2area(ΔAPC)
Tick the correct answer and justify:
Q8. ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the area of triangles ABC and BDE is
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 1 : 4
Solution: Given, ΔABC and ΔBDE are two equilateral triangle. D is the midpoint of BC.
∴ BD = DC = 1/2BC
Let each side of triangle is 2a.
As, ΔABC ~ ΔBDE
∴ Area(ΔABC)/Area(ΔBDE) = AB2/BD2 = (2a)2/(a)2 = 4a2/a2 = 4/1 = 4:1
Hence, the correct answer is (C).
9. Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(A) 2 : 3
(B) 4 : 9
(C) 81 : 16
(D) 16 : 81
Solution: Given, Sides of two similar triangles are in the ratio 4 : 9.
Let ABC and DEF are two similar triangles, such that,
ΔABC ~ ΔDEF
And AB/DE = AC/DF = BC/EF = 4/9
As, the ratio of the areas of these triangles will be equal to the square of the ratio of the corresponding sides,
∴ Area(ΔABC)/Area(ΔDEF) = AB2/DE2
∴ Area(ΔABC)/Area(ΔDEF) = (4/9)2 = 16/81 = 16:81
Hence, the correct answer is (D).
Q1. Sides of triangles are given below. Determine which of them are right triangles? In case of a right triangle, write the length of its hypotenuse.
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm
Solution:
(i) Given, sides of the triangle are 7 cm, 24 cm, and 25 cm.
Squaring the lengths of the sides of the, we will get 49, 576, and 625.
49 + 576 = 625
(7)2 + (24)2 = (25)2
Therefore, the above equation satisfies, Pythagoras theorem. Hence, it is right angled triangle.
Length of Hypotenuse = 25 cm
(ii) Given, sides of the triangle are 3 cm, 8 cm, and 6 cm.
Squaring the lengths of these sides, we will get 9, 64, and 36.
Clearly, 9 + 36 ≠ 64
Or, 32 + 62 ≠ 82
Therefore, the sum of the squares of the lengths of two sides is not equal to the square of the length of the hypotenuse.
Hence, the given triangle does not satisfies Pythagoras theorem.
(iii) Given, sides of triangle’s are 50 cm, 80 cm, and 100 cm.
Squaring the lengths of these sides, we will get 2500, 6400, and 10000.
However, 2500 + 6400 ≠ 10000
Or, 502 + 802 ≠ 1002
As you can see, the sum of the squares of the lengths of two sides is not equal to the square of the length of the third side.
Therefore, the given triangle does not satisfies Pythagoras theorem.
Hence, it is not a right triangle.
(iv) Given, sides are 13 cm, 12 cm, and 5 cm.
Squaring the lengths of these sides, we will get 169, 144, and 25.
Thus, 144 +25 = 169
Or, 122 + 52 = 132
The sides of the given triangle are satisfying Pythagoras theorem.
Therefore, it is a right triangle.
Hence, length of the hypotenuse of this triangle is 13 cm.
Q2. PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM × MR.
Solution: Given, ΔPQR is right angled at P is a point on QR such that PM ⊥QR
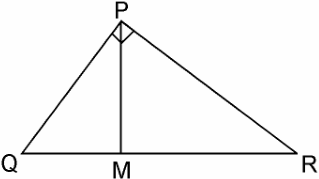
We have to prove, PM2 = QM × MR
In ΔPQM, by Pythagoras theorem
PQ2 = PM2 + QM2
Or, PM2 = PQ2 – QM2 ……………………………..(i)
In ΔPMR, by Pythagoras theorem
PR2 = PM2 + MR2
Or, PM2 = PR2 – MR2 ………………………………………..(ii)
Adding equation, (i) and (ii), we get,
2PM2 = (PQ2 + PM2) – (QM2 + MR2)
= QR2 – QM2 – MR2 [∴ QR2 = PQ2 + PR2]
= (QM + MR)2 – QM2 – MR2
= 2QM × MR
∴ PM2 = QM × MR
3. In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that
(i) AB2 = BC × BD
(ii) AC2 = BC × DC
(iii) AD2 = BD × CD

Solution:
(i) In ΔADB and ΔCAB,
∠DAB = ∠ACB (Each 90°)
∠ABD = ∠CBA (Common angles)
∴ ΔADB ~ ΔCAB [AA similarity criterion]
⇒ AB/CB = BD/AB
⇒ AB2 = CB × BD
(ii) Let ∠CAB = x
In ΔCBA,
∠CBA = 180° – 90° – x
∠CBA = 90° – x
Similarly, in ΔCAD
∠CAD = 90° – ∠CBA
= 90° – x
∠CDA = 180° – 90° – (90° – x)
∠CDA = x
In ΔCBA and ΔCAD, we have
∠CBA = ∠CAD
∠CAB = ∠CDA
∠ACB = ∠DCA (Each 90°)
∴ ΔCBA ~ ΔCAD [AAA similarity criterion]
⇒ AC/DC = BC/AC
⇒ AC2 = DC × BC
(iii) In ΔDCA and ΔDAB,
∠DCA = ∠DAB (Each 90°)
∠CDA = ∠ADB (common angles)
∴ ΔDCA ~ ΔDAB [AA similarity criterion]
⇒ DC/DA = DA/DA
⇒ AD2 = BD × CD
4. ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2.
Solution: Given, ΔABC is an isosceles triangle right angled at C.
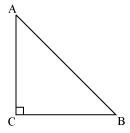
In ΔACB, ∠C = 90°
AC = BC (By isosceles triangle property)
AB2 = AC2 + BC2 [By Pythagoras theorem]
= AC2 + AC2 [Since, AC = BC]
AB2 = 2AC2
Q5. ABC is an isosceles triangle with AC = BC. If AB2 = 2AC2, prove that ABC is a right triangle.
Solution: Given, ΔABC is an isosceles triangle having AC = BC and AB2 = 2AC2
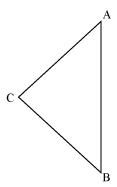
In ΔACB,
AC = BC
AB2 = 2AC2
AB2 = AC2 + AC2
= AC2 + BC2 [Since, AC = BC]
Hence, by Pythagoras theorem ΔABC is right angle triangle.
6. ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Solution: Given, ABC is an equilateral triangle of side 2a.
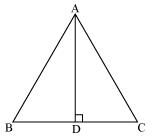
Draw, AD ⊥ BC
In ΔADB and ΔADC,
AB = AC
AD = AD
∠ADB = ∠ADC [Both are 90°]
Therefore, ΔADB ≅ ΔADC by RHS congruence.
Hence, BD = DC [by CPCT]
In right angled ΔADB,
AB2 = AD2 + BD2
(2a)2 = AD2 + a2
⇒ AD2 = 4a2 – a2
⇒ AD2 = 3a2
⇒ AD = √3a
7. Prove that the sum of the squares of the sides of rhombus is equal to the sum of the squares of its diagonals.
Solution: Given, ABCD is a rhombus whose diagonals AC and BD intersect at O.
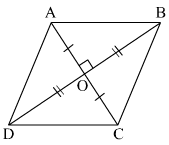
We have to prove, as per the question,
AB2 + BC2 + CD2 + AD2 = AC2 + BD2
Since, the diagonals of a rhombus bisect each other at right angles.
Therefore, AO = CO and BO = DO
In ΔAOB,
∠AOB = 90°
AB2 = AO2 + BO2 …………………….. (i) [By Pythagoras theorem]
Similarly,
AD2 = AO2 + DO2 …………………….. (ii)
DC2 = DO2 + CO2 …………………….. (iii)
BC2 = CO2 + BO2 …………………….. (iv)
Adding equations (i) + (ii) + (iii) + (iv), we get,
AB2 + AD2 + DC2 + BC2 = 2(AO2 + BO2 + DO2 + CO2 )
= 4AO2 + 4BO2 [Since, AO = CO and BO =DO]
= (2AO)2 + (2BO)2 = AC2 + BD2
AB2 + AD2 + DC2 + BC2 = AC2 + BD2
Hence, proved.
8. In Fig. 6.54, O is a point in the interior of a triangle.
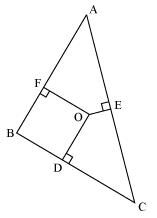
ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that:
(i) OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2 ,
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2.
Solution: Given, in ΔABC, O is a point in the interior of a triangle.
And OD ⊥ BC, OE ⊥ AC and OF ⊥ AB.
Join OA, OB and OC
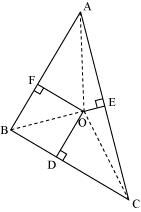
(i) By Pythagoras theorem in ΔAOF, we have
OA2 = OF2 + AF2
Similarly, in ΔBOD
OB2 = OD2 + BD2
Similarly, in ΔCOE
OC2 = OE2 + EC2
Adding these equations,
OA2 + OB2 + OC2 = OF2 + AF2 + OD2 + BD2 + OE2 + EC2
OA2 + OB2 + OC2 – OD2 – OE2 – OF2 = AF2 + BD2 + CE2.
(ii) AF2 + BD2 + EC2 = (OA2 – OE2) + (OC2 – OD2) + (OB2 – OF2)
∴ AF2 + BD2 + CE2 = AE2 + CD2 + BF2.
Q9. A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
Solution: Given, a ladder 10 m long reaches a window 8 m above the ground.
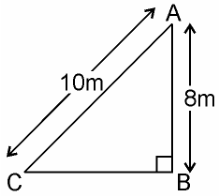
Let BA be the wall and AC be the ladder,
Therefore, by Pythagoras theorem,
AC2 = AB2 + BC2
102 = 82 + BC2
BC2 = 100 – 64
BC2 = 36
BC = 6m
Therefore, the distance of the foot of the ladder from the base of the wall is 6 m.
Q10. A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
Solution: Given, a guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end.

Let AB be the pole and AC be the wire.
By Pythagoras theorem,
AC2 = AB2 + BC2
242 = 182 + BC2
BC2 = 576 – 324
BC2 = 252
BC = 6√7m
Therefore, the distance from the base is 6√7m.
Q11. An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after hours?
hours?
Solution: Given,
Speed of first aeroplane = 1000 km/hr
Distance covered by first aeroplane flying due north in hours (OA) = 100 × 3/2 km = 1500 km
hours (OA) = 100 × 3/2 km = 1500 km
Speed of second aeroplane = 1200 km/hr
Distance covered by second aeroplane flying due west in hours (OB) = 1200 × 3/2 km = 1800 km
hours (OB) = 1200 × 3/2 km = 1800 km
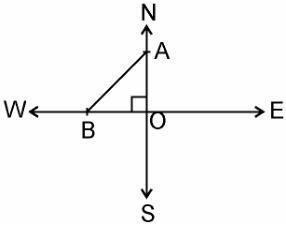
In right angle ΔAOB, by Pythagoras Theorem,
AB2 = AO2 + OB2
⇒ AB2 = (1500)2 + (1800)2
⇒ AB = √(2250000 + 3240000)
= √5490000
⇒ AB = 300√61 km
Hence, the distance between two aeroplanes will be 300√61 km.
Q12. Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
Solution: Given, Two poles of heights 6 m and 11 m stand on a plane ground.
And distance between the feet of the poles is 12 m.
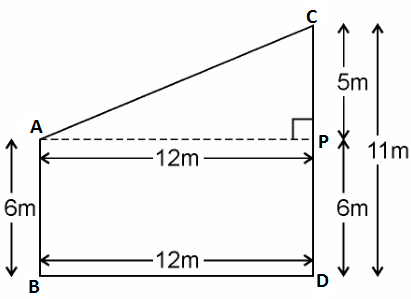
Let AB and CD be the poles of height 6m and 11m.
Therefore, CP = 11 – 6 = 5m
From the figure, it can be observed that AP = 12m
By Pythagoras theorem for ΔAPC, we get,
AP2 = PC2 + AC2
(12m)2 + (5m)2 = (AC)2
AC2 = (144+25)m2 = 169 m2
AC = 13m
Therefore, the distance between their tops is 13 m.
Q13. D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2.
Solution: Given, D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C.
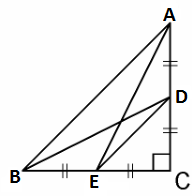
By Pythagoras theorem in ΔACE, we get
AC2 + CE2 = AE2 ………………………………………….(i)
In ΔBCD, by Pythagoras theorem, we get
BC2 + CD2 = BD2 ………………………………..(ii)
From equations (i) and (ii), we get,
AC2 + CE2 + BC2 + CD2 = AE2 + BD2 …………..(iii)
In ΔCDE, by Pythagoras theorem, we get
DE2 = CD2 + CE2
In ΔABC, by Pythagoras theorem, we get
AB2 = AC2 + CB2
Putting the above two values in equation (iii), we get
DE2 + AB2 = AE2 + BD2.
Q14. The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3CD (see Figure). Prove that 2AB2 = 2AC2 + BC2.
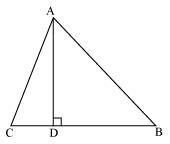
Solution: Given, the perpendicular from A on side BC of a Δ ABC intersects BC at D such that;
DB = 3CD.
In Δ ABC,
AD ⊥BC and BD = 3CD
In right angle triangle, ADB and ADC, by Pythagoras theorem,
AB2 = AD2 + BD2 ……………………….(i)
AC2 = AD2 + DC2 ……………………………..(ii)
Subtracting equation (ii) from equation (i), we get
AB2 – AC2 = BD2 – DC2
= 9CD2 – CD2 [Since, BD = 3CD]
= 9CD2 = 8(BC/4)2 [Since, BC = DB + CD = 3CD + CD = 4CD]
Therefore, AB2 – AC2 = BC2/2
⇒ 2(AB2 – AC2) = BC2
⇒ 2AB2 – 2AC2 = BC2
∴ 2AB2 = 2AC2 + BC2.
Q15. In an equilateral triangle ABC, D is a point on side BC such that BD = 1/3BC. Prove that 9AD2 = 7AB2.
Solution: Given, ABC is an equilateral triangle.
And D is a point on side BC such that BD = 1/3BC
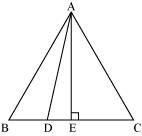
Let the side of the equilateral triangle be a, and AE be the altitude of ΔABC.
∴ BE = EC = BC/2 = a/2
And, AE = a√3/2
Given, BD = 1/3BC
∴ BD = a/3
DE = BE – BD = a/2 – a/3 = a/6
In ΔADE, by Pythagoras theorem,
AD2 = AE2 + DE2

⇒ 9 AD2 = 7 AB2
Q16. In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Solution: Given, an equilateral triangle say ABC,
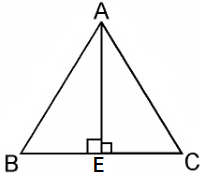
Let the sides of the equilateral triangle be of length a, and AE be the altitude of ΔABC.
∴ BE = EC = BC/2 = a/2
In ΔABE, by Pythagoras Theorem, we get
AB2 = AE2 + BE2

4AE2 = 3a2
⇒ 4 × (Square of altitude) = 3 × (Square of one side)
Hence, proved.
17. Tick the correct answer and justify: In ΔABC, AB = 6√3 cm, AC = 12 cm and BC = 6 cm.
The angle B is:
(A) 120°
(B) 60°
(C) 90°
(D) 45°
Solution: Given, in ΔABC, AB = 6√3 cm, AC = 12 cm and BC = 6 cm.
We can observe that,
AB2 = 108
AC2 = 144
And, BC2 = 36
AB2 + BC2 = AC2
The given triangle, ΔABC, is satisfying Pythagoras theorem.
Therefore, the triangle is a right triangle, right-angled at B.
∴ ∠B = 90°
Hence, the correct answer is (C).
1. In Figure, PS is the bisector of ∠ QPR of ∆ PQR. Prove that QS/PQ = SR/PR
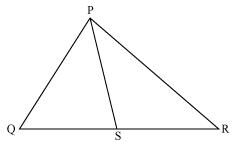
Solution:
Let us draw a line segment RT parallel to SP which intersects extended line segment QP at point T.
Given, PS is the angle bisector of ∠QPR. Therefore,
∠QPS = ∠SPR………………………………..(i)
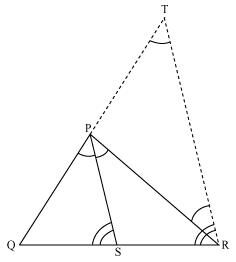
As per the constructed figure,
∠SPR=∠PRT(Since, PS||TR)……………(ii)
∠QPS = ∠QRT(Since, PS||TR) …………..(iii)
From the above equations, we get,
∠PRT=∠QTR
Therefore,
PT=PR
In △QTR, by basic proportionality theorem,
QS/SR = QP/PT
Since, PT=TR
Therefore,
QS/SR = PQ/PR
Q2. In Fig. 6.57, D is a point on hypotenuse AC of ∆ABC, such that BD ⊥AC, DM ⊥ BC and DN ⊥ AB. Prove that: (i) DM2 = DN . MC (ii) DN2 = DM . AN.
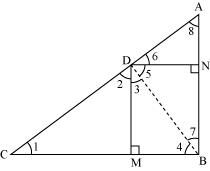
Let us join Point D and B.
(i) Given,
BD ⊥AC, DM ⊥ BC and DN ⊥ AB
Now from the figure we have,
DN || CB, DM || AB and ∠B = 90 °
Therefore, DMBN is a rectangle.
So, DN = MB and DM = NB
The given condition which we have to prove, is when D is the foot of the perpendicular drawn from B to AC.
∴ ∠CDB = 90° ⇒ ∠2 + ∠3 = 90° ……………………. (i)
In ∆CDM, ∠1 + ∠2 + ∠DMC = 180°
⇒ ∠1 + ∠2 = 90° …………………………………….. (ii)
In ∆DMB, ∠3 + ∠DMB + ∠4 = 180°
⇒ ∠3 + ∠4 = 90° …………………………………….. (iii)
From equation (i) and (ii), we get
∠1 = ∠3
From equation (i) and (iii), we get
∠2 = ∠4
In ∆DCM and ∆BDM,
∠1 = ∠3 (Already Proved)
∠2 = ∠4 (Already Proved)
∴ ∆DCM ∼ ∆BDM (AA similarity criterion)
BM/DM = DM/MC
DN/DM = DM/MC (BM = DN)
⇒ DM2 = DN × MC
Hence, proved.
(ii) In right triangle DBN,
∠5 + ∠7 = 90° ……………….. (iv)
In right triangle DAN,
∠6 + ∠8 = 90° ………………… (v)
D is the point in triangle, which is foot of the perpendicular drawn from B to AC.
∴ ∠ADB = 90° ⇒ ∠5 + ∠6 = 90° ………….. (vi)
From equation (iv) and (vi), we get,
∠6 = ∠7
From equation (v) and (vi), we get,
∠8 = ∠5
In ∆DNA and ∆BND,
∠6 = ∠7 (Already proved)
∠8 = ∠5 (Already proved)
∴ ∆DNA ∼ ∆BND (AA similarity criterion)
AN/DN = DN/NB
⇒ DN2 = AN × NB
⇒ DN2 = AN × DM (Since, NB = DM)
Q3. In Figure, ABC is a triangle in which ∠ABC > 90° and AD ⊥ CB produced. Prove that
AC2= AB2+ BC2+ 2 BC.BD.
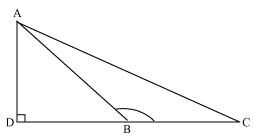
Solution: By applying Pythagoras Theorem in ∆ADB, we get,
AB2 = AD2 + DB2 ……………………… (i)
Again, by applying Pythagoras Theorem in ∆ACD, we get,
AC2 = AD2 + DC2
AC2 = AD2 + (DB + BC) 2
AC2 = AD2 + DB2 + BC2 + 2DB × BC
From equation (i), we can write,
AC2 = AB2 + BC2 + 2DB × BC
Q4. In Figure, ABC is a triangle in which ∠ ABC < 90° and AD ⊥ BC. Prove that
AC2= AB2+ BC2 – 2 BC.BD.
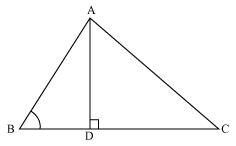
Solution: By applying Pythagoras Theorem in ∆ADB, we get,
AB2 = AD2 + DB2
We can write it as;
⇒ AD2 = AB2 − DB2 ……………….. (i)
By applying Pythagoras Theorem in ∆ADC, we get,
AD2 + DC2 = AC2
From equation (i),
AB2 − BD2 + DC2 = AC2
AB2 − BD2 + (BC − BD) 2 = AC2
AC2 = AB2 − BD2 + BC2 + BD2 −2BC × BD
AC2= AB2 + BC2 − 2BC × BD
Hence, proved.
5. In Figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that :
(i) AC2 = AD2 + BC.DM + 2 (BC/2) 2
(ii) AB2 = AD2 – BC.DM + 2 (BC/2) 2
(iii) AC2 + AB2 = 2 AD2 + ½ BC2
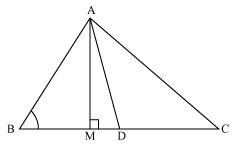
Solution:
(i) By applying Pythagoras Theorem in ∆AMD, we get,
AM2 + MD2 = AD2 ………………. (i)
Again, by applying Pythagoras Theorem in ∆AMC, we get,
AM2 + MC2 = AC2
AM2 + (MD + DC) 2 = AC2
(AM2 + MD2 ) + DC2 + 2MD.DC = AC2
From equation(i), we get,
AD2 + DC2 + 2MD.DC = AC2
Since, DC=BC/2, thus, we get,
AD2 + (BC/2) 2 + 2MD.(BC/2) 2 = AC2
AD2 + (BC/2) 2 + 2MD × BC = AC2
Hence, proved.
(ii) By applying Pythagoras Theorem in ∆ABM, we get;
AB2 = AM2 + MB2
=> (AD2 − DM2 ) + MB2
=> (AD2 − DM2 ) + (BD − MD) 2
=> AD2 − DM2 + BD2 + MD2 − 2BD × MD
=> AD2 + BD2 − 2BD × MD
=> AD2 + (BC/2) 2 – 2(BC/2) MD
=> AD2 + (BC/2) 2 – BC MD
Hence, proved.
(iii) By applying Pythagoras Theorem in ∆ABM, we get,
AM2 + MB2 = AB2 ………………….… (i)
By applying Pythagoras Theorem in ∆AMC, we get,
AM2 + MC2 = AC2 …………………..… (ii)
Adding both the equations (i) and (ii), we get,
2AM2 + MB2 + MC2 = AB2 + AC2
2AM2 + (BD − DM) 2 + (MD + DC) 2 = AB2 + AC2
2AM2+BD2 + DM2 − 2BD.DM + MD2 + DC2 + 2MD.DC = AB2 + AC2
2AM2 + 2MD2 + BD2 + DC2 + 2MD (− BD + DC) = AB2 + AC2
2(AM2+ MD2) + (BC/2) 2 + (BC/2) 2 + 2MD(-BC/2 + BC/2) 2 = AB2 + AC2
2AD2 + BC2/2 = AB2 + AC2
Q6. Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
Solution:
Let us consider, ABCD be a parallelogram. Now, draw perpendicular DE on extended side of AB, and draw a perpendicular AF meeting DC at point F.
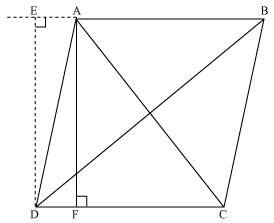
By applying Pythagoras Theorem in ∆DEA, we get,
DE2 + EA2 = DA2 ……………….… (i)
By applying Pythagoras Theorem in ∆DEB, we get,
DE2 + EB2 = DB2
DE2 + (EA + AB) 2 = DB2
(DE2 + EA2 ) + AB2 + 2EA × AB = DB2
DA2 + AB2 + 2EA × AB = DB2 ……………. (ii)
By applying Pythagoras Theorem in ∆ADF, we get,
AD2 = AF2 + FD2
Again, applying Pythagoras theorem in ∆AFC, we get,
AC2 = AF2 + FC2 = AF2 + (DC − FD) 2
= AF2 + DC2 + FD2 − 2DC × FD
= (AF2 + FD2 ) + DC2 − 2DC × FD AC2
AC2= AD2 + DC2 − 2DC × FD ………………… (iii)
Since ABCD is a parallelogram,
AB = CD ………………….…(iv)
And BC = AD ………………. (v)
In ∆DEA and ∆ADF,
∠DEA = ∠AFD (Each 90°)
∠EAD = ∠ADF (EA || DF)
AD = AD (Common Angles)
∴ ∆EAD ≅ ∆FDA (AAS congruence criterion)
⇒ EA = DF ……………… (vi)
Adding equations (i) and (iii), we get,
DA2 + AB2 + 2EA × AB + AD2 + DC2 − 2DC × FD = DB2 + AC2
DA2 + AB2 + AD2 + DC2 + 2EA × AB − 2DC × FD = DB2 + AC2
From equation (iv) and (vi),
BC2 + AB2 + AD2 + DC2 + 2EA × AB − 2AB × EA = DB2 + AC2
AB2 + BC2 + CD2 + DA2 = AC2 + BD2
7. In Figure, two chords AB and CD intersect each other at the point P. Prove that :
(i) ∆APC ~ ∆ DPB
(ii) AP . PB = CP . DP
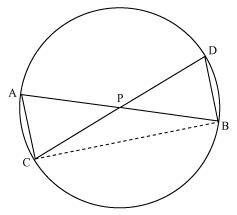
Solution: Firstly, let us join CB, in the given figure.
(i) In ∆APC and ∆DPB,
∠APC = ∠DPB (Vertically opposite angles)
∠CAP = ∠BDP (Angles in the same segment for chord CB)
Therefore,
∆APC ∼ ∆DPB (AA similarity criterion)
(ii) In the above, we have proved that ∆APC ∼ ∆DPB
We know that the corresponding sides of similar triangles are proportional.
∴ AP/DP = PC/PB = CA/BD
⇒AP/DP = PC/PB
∴AP. PB = PC. DP
Hence, proved.
8. In Fig. 6.62, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that:
(i) ∆ PAC ~ ∆ PDB
(ii) PA . PB = PC . PD.
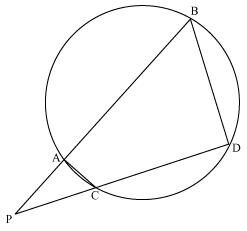
Solution:
(i) In ∆PAC and ∆PDB,
∠P = ∠P (Common Angles)
As we know, exterior angle of a cyclic quadrilateral is ∠PCA and ∠PBD is opposite interior angle, which are both equal.
∠PAC = ∠PDB
Thus, ∆PAC ∼ ∆PDB(AA similarity criterion)
(ii) We have already proved above,
∆APC ∼ ∆DPB
We know that the corresponding sides of similar triangles are proportional.
Therefore,
AP/DP = PC/PB = CA/BD
AP/DP = PC/PB
∴ AP. PB = PC. DP
Q9. In Figure, D is a point on side BC of ∆ ABC such that BD/CD = AB/AC. Prove that AD is the bisector of ∠ BAC.
Solutions: In the given figure, let us extend BA to P such that;
AP = AC.
Now join PC.

Given, BD/CD = AB/AC
⇒ BD/CD = AP/AC
By using the converse of basic proportionality theorem, we get,
AD || PC
∠BAD = ∠APC (Corresponding angles) ……………….. (i)
And, ∠DAC = ∠ACP (Alternate interior angles) …….… (ii)
By the new figure, we have;
AP = AC
⇒ ∠APC = ∠ACP ……………………. (iii)
On comparing equations (i), (ii), and (iii), we get,
∠BAD = ∠APC
Therefore, AD is the bisector of the angle BAC.
Q10. Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out (see Figure)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?

Solution:
Let us consider, AB is the height of the tip of the fishing rod from the water surface and BC is the
horizontal distance of the fly from the tip of the fishing rod. Therefore, AC is now the length of the string.
To find AC, we have to use Pythagoras theorem in ∆ABC, is such way;
AC2 = AB2+ BC2
AB2 = (1.8 m) 2 + (2.4 m) 2
AB2 = (3.24 + 5.76) m2
AB2 = 9.00 m2
⟹ AB = √9 m = 3m
Thus, the length of the string out is 3 m.
As its given, she pulls the string at the rate of 5 cm per second.
Therefore, string pulled in 12 seconds = 12 × 5 = 60 cm = 0.6
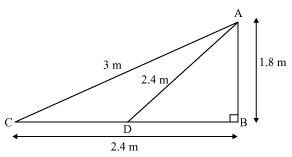
Let us say now, the fly is at point D after 12 seconds.
Length of string out after 12 seconds is AD.
AD = AC − String pulled by Nazima in 12 seconds
= (3.00 − 0.6) m
= 2.4 m
In ∆ADB, by Pythagoras Theorem,
AB2 + BD2 = AD2
(1.8 m) 2 + BD2 = (2.4 m) 2
BD2 = (5.76 − 3.24) m2 = 2.52 m2
BD = 1.587 m
Horizontal distance of fly = BD + 1.2 m
= (1.587 + 1.2) m = 2.787 m
= 2.79 m



