- The circle, the square, the rectangle, the quadrilateral and the triangle are examples of plane figures.
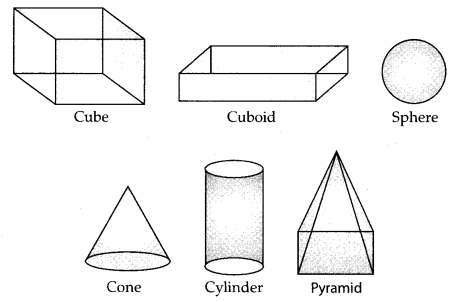
- The cube, the cuboid, the sphere, the cylinder, the cone and the pyramid are examples of solid shapes.
- Plane figures are of two-dimensions (2-D) and the solid shapes are of three dimensions (3-D).
Solid Shapes
- Solid shapes have length, breadth or width and depth or height.
- They are called 3D or three-dimensional shapes.
- Example: Cuboids, Cylinders, Spheres and Pyramids.
Nets for Building 3-D Shapes
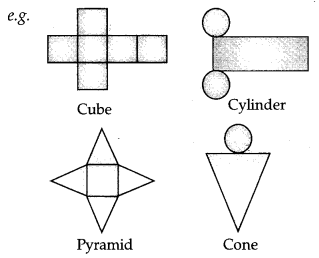
A net is a skeleton outline of a solid that can be folded to make it. The same solid can have several types of nets.
Drawing Solids on a Flat Surface
Solid shapes can be drawn on a flat surface (like paper) realistically. We call this 2-D representation of a 3-D solid.
Oblique Sketches
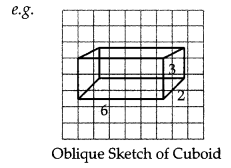
An oblique sketch does not have proportional lengths. Still, it conveys all important aspects of the appearance of the solid.
Isometric Sketches
An isometric sketch is drawn on an isometric dot paper. In an isometric sketch of the solid, the measurements are kept proportional.
Visualising Solid Objects
Visualising solid shapes is a very useful skill. For this, the ability to see ‘hidden’ parts of the solid shape is required.
Viewing Different Solutions of a Solid
One Way to View an Object is by Cutting or Slicing
Slicing Game: It results in the cross-section of the solid.
A Kitchen Play
Another Way is by Shadow Play
A Third Way is by Looking at it from Certain Angles to Get Different Views
A third way is to look at the shape from different angles; the front-view, the side-view and the top-view. These provide a lot of information about the shape observed.
Cube, cuboid, sphere, cylinder, cone and the pyramid are examples of solid shapes.
The corners of solid shape are called its vertices, the line segments of its skeleton are its edges, and its flat surfaces are its faces.
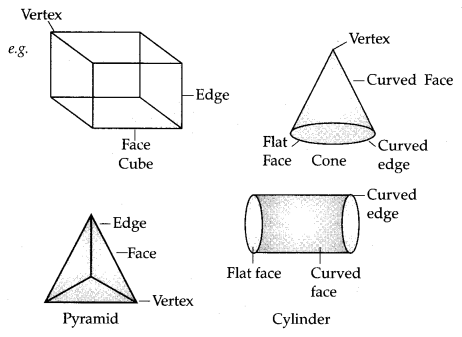
A figure or shape whose faces are polygons (triangles, quadrilaterals, etc.) is called a polyhedron. If F, E and V denote respectively the number of faces, edges and vertices of a polyhedron, then F – E + V = 2. This is called Euler’s Formula.
| Name of Solid | Number of Faces | Number of Vertices | Number of Edges |
| Cuboid | 6 | 8 | 12 |
| Cube | 6 | 8 | 12 |
| Cylinder | 3 | Nil | 2 |
| Cone | 2 | 1 | 1 |
| Sphere | 1 | Nil | Nil |
| Triangular Pyramid | 4 | 4 | 6 |
A net is a skeleton – outline of a solid that can be folded to .make it. The same solid can have several types of nets.
An oblique sketch does not have proportional lengths. Still it conveys all important aspects of the appearance of the solid.
We can view a three dimensional solid by different ways such as
(i) Slicing: When we give a ‘cut’ or ‘slice’, we get a plane face. This plane face is called a ‘Cross – section’ and its boundary is a plane curve.
(ii) Shadowing: When a circular plate or cup is placed in the open and the sun at the noon, is just right above it. Whereas, during evening, it is just left above it. We will see the shadows of a cup.
(iii) Looking a solid from Different Angles: The front view and the top view which can provide a lots of information about the shape observed. We can see three views (i.e. front view, side view, and top view) of a house


