Ex 3.1
Question 1.
How will you describe the position of a table lamp on your study table to another person?
Solution:
To describe the position of a table lamp placed on the table, let us consider the table lamp as P and the table as a plane.
Now choose two perpendicular edges of the table as the axes OX and OY.
Measure the perpendicular distance ‘a’cm of P (lamp) from OY. Measure the perpendicular distance ‘b’ cm of P (lamp) from OX.
Thus, the position of the table lamp P is described by the ordered pair (a, b).

Question 2.
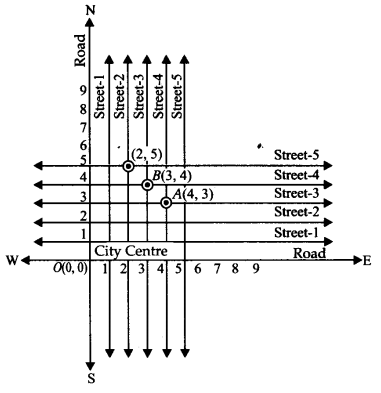
(Street Plan): A city has two main roads which cross each other at the centre of the city. These two roads are along the North-South direction and East-West direction. All other streets of the city run parallel to these roads and are 200 m apart. There are 5 streets in each direction. Using 1 cm = 200 m, draw a model of the city on your notebook. Represent the roads/streets by single lines.
There are many cross-streets in your model. A particular cross-street is made by two streets, one running in the North-South direction and another in the East-West direction. Each cross street is referred to in the following manner: If the 2nd street running in the North-South direction and 5th in the East-West direction meet at some crossing, then we will call this cross-street (2,5). Using this convention, find:
(i) how many cross-streets can be referred to as (4,3).
(ii) how many cross-streets can be referred to as (3,4).
Solution:
(i) A unique cross street as shown by the point A(4, 3).
(ii) A unique cross street as shown by the point B(3,4).
The two cross streets are uniquely found because of the two reference lines we have used for locating them.
Ex 3.2
Question 1.
Write the answer of each of the following questions:
(i) What is the name of horizontal and the vertical lines drawn to determine the position of any point in the Cartesian plane?
(ii) What is the name of each part of the plane formed by these two lines?
(iii) Write the name of the point where these two lines intersect.
Solution:
(i) The name of horizontal and vertical lines drawn to determine the position of any point in the Cartesian plane is x-axis and y-axis respectively.
(ii) The name of each part of the plane formed by these two lines x-axis and y-axis is quadrants.
(iii) The point where these two lines intersect is called the origin.
Question 2.
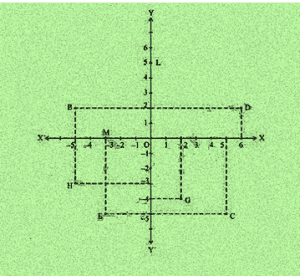
See Fig.3.14, and write the following:
i. The coordinates of B.
ii. The coordinates of C.
iii. The point identified by the coordinates (–3, –5).
iv. The point identified by the coordinates (2, – 4).
v. The abscissa of the point D.
vi. The ordinate of the point H.
vii. The coordinates of the point L.
viii. The coordinates of the point M.
Solution:
i. The co-ordinates of B is (−5, 2).
ii. The co-ordinates of C is (5, −5).
iii. The point identified by the coordinates (−3, −5) is E.
iv. The point identified by the coordinates (2, −4) is G.
v. Abscissa means x co-ordinate of point D. So, abscissa of the point D is 6.
vi. Ordinate means y coordinate of point H. So, ordinate of point H is -3.
vii. The co-ordinates of the point L is (0, 5).
viii. The co-ordinates of the point M is (−3, 0).
Ex 3.3
Question 1.

Question 2.

The points to plotted on the (x, y) are:
i. (-2, 8)
ii. (-1, 7)
iii. (0, -1.25)
iv. (1, 3)
v. (3, -1)
On the graph mark X-axis and Y-axis. Mark the meeting point as O.
Now, Let 1 unit = 1 cm


