NCERT Solutions Ch- 6 Lines and Angles

Ex 6.1

Question 1
In figure, lines AB and CD intersect at 0. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.

Solution:
Since AB is a straight line,
∴ ∠AOC + ∠COE + ∠EOB = 180°
or (∠AOC + ∠BOE) + ∠COE = 180° or 70° + ∠COE = 180° [ ∵∠AOC + ∠BOE = 70° (Given)]
or ∠COE = 180° – 70° = 110°
∴ Reflex ∠COE = 360° – 110° = 250°
Also, AB and CD intersect at O.
∴∠COA = ∠BOD [Vertically opposite angles]
But ∠BOD = 40° [Given]
∴ ∠COA = 40°
Also, ∠AOC + ∠BOE = 70°
∴ 40° + ∠BOE = 70° or ∠BOE = 70° -40° = 30°
Thus, ∠BOE = 30° and reflex ∠COE = 250°.

Question 2.
In figure, lines XY and MN intersect at 0. If ∠POY = 90° , and a : b = 2 : 3. find c.

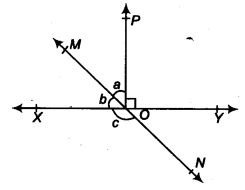
Solution:
Since XOY is a straight line.
∴ b+a+∠POY= 180°
But ∠POY = 90° [Given]
∴ b + a = 180° – 90° = 90° …(i)
Also a : b = 2 : 3 ⇒ b = $frac { 3a }{ 2 }$ …(ii)
Now from (i) and (ii), we get
$frac { 3a }{ 2 }$ + A = 90°
⇒ $frac { 5a }{ 2 }$ = 90°
⇒ a = $frac { { 90 }^{ circ } }{ 5 } times 2quad =quad { 36 }^{ circ }$ = 36°
From (ii), we get
b = $frac { 3 }{ 2 }$ x 36° = 54°
Since XY and MN interstect at O,
∴ c = [a + ∠POY] [Vertically opposite angles]
or c = 36° + 90° = 126°
Thus, the required measure of c = 126°.

Question 3.
In figure, ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.

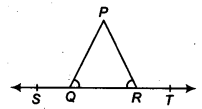
Solution:
ST is a straight line.
∴ ∠PQR + ∠PQS = 180° …(1) [Linear pair]
Similarly, ∠PRT + ∠PRQ = 180° …(2) [Linear Pair]
From (1) and (2), we have
∠PQS + ∠PQR = ∠PRT + ∠PRQ
But ∠PQR = ∠PRQ [Given]
∴ ∠PQS = ∠PRT

Question 4.

In Fig. 6.16, if x+y = w+z, then prove that AOB is a line.

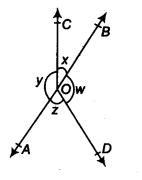
Solution:

For proving AOB is a straight line, we will have to prove x+y is a linear pair

i.e. x+y = 180°

We know that the angles around a point are 360° so,

x+y+w+z = 360°

In the question, it is given that,

x+y = w+z

So, (x+y)+(x+y) = 360°

2(x+y) = 360°

∴ (x+y) = 180° (Hence proved).

Question 5.

In Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ROS = ½ (QOS – POS).

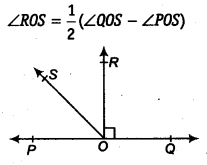
Solution:

In the question, it is given that (OR ⊥ PQ) and POQ = 180°

So, POS+ROS+ROQ = 180°

Now, POS+ROS = 180°- 90° (Since POR = ROQ = 90°)

∴ POS + ROS = 90°

Now, QOS = ROQ+ROS

It is given that ROQ = 90°,

∴ QOS = 90° +ROS

Or, QOS – ROS = 90°

As POS + ROS = 90° and QOS – ROS = 90°, we get

POS + ROS = QOS – ROS

2 ROS + POS = QOS

Or, ROS = ½ (QOS – POS) (Hence proved).

Question 6.

It is given that XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ZYP, find XYQ and reflex QYP.

Solution:

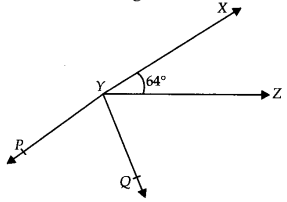
Here, XP is a straight line

So, XYZ +ZYP = 180°

Putting the value of XYZ = 64° we get,

64° +ZYP = 180°

∴ ZYP = 116°

From the diagram, we also know that ZYP = ZYQ + QYP

Now, as YQ bisects ZYP,

ZYQ = QYP

Or, ZYP = 2ZYQ

∴ ZYQ = QYP = 58°

Again, XYQ = XYZ + ZYQ

By putting the value of XYZ = 64° and ZYQ = 58° we get.

XYQ = 64°+58°

Or, XYQ = 122°

Now, reflex QYP = 180°+XYQ

We computed that the value of XYQ = 122°.

So,

QYP = 180°+122°

∴ QYP = 302°

Ex 6.2

1. In Fig. 6.28, find the values of x and y and then show that AB CD.

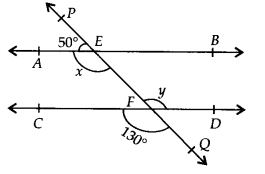
Solution:

We know that a linear pair is equal to 180°.

So, x+50° = 180°

∴ x = 130°

We also know that vertically opposite angles are equal.

So, y = 130°

In two parallel lines, the alternate interior angles are equal. In this,

x = y = 130°

This proves that alternate interior angles are equal and so, AB CD.

2. In Fig. 6.29, if AB CD, CD EF and y : z = 3 : 7, find x.

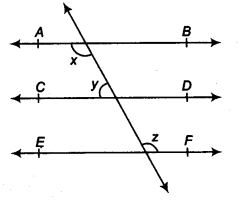
Solution:

It is known that AB CD and CDEF

As the angles on the same side of a transversal line sums up to 180°,

x + y = 180° —–(i)

Also,

O = z (Since they are corresponding angles)

and, y +O = 180° (Since they are a linear pair)

So, y+z = 180°

Now, let y = 3w and hence, z = 7w (As y : z = 3 : 7)

∴ 3w+7w = 180°

Or, 10 w = 180°

So, w = 18°

Now, y = 3×18° = 54°

and, z = 7×18° = 126°

Now, angle x can be calculated from equation (i)

x+y = 180°

Or, x+54° = 180°

∴ x = 126°

3. In Fig. 6.30, if AB CD, EF ⊥ CD and GED = 126°, find AGE, GEF and FGE.

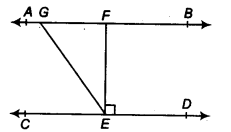
Solution:

Since AB CD, GE is a transversal.

It is given that GED = 126°

So, GED = AGE = 126° (As they are alternate interior angles)

Also,

GED = GEF +FED

As EF⊥ CD, FED = 90°

∴ GED = GEF+90°

Or, GEF = 126° – 90° = 36°

Again, FGE +GED = 180° (Transversal)

Putting the value of GED = 126° we get,

FGE = 54°

So,

AGE = 126°

GEF = 36° and

FGE = 54°

4. In Fig. 6.31, if PQ ST, PQR = 110° and RST = 130°, find QRS.

[Hint : Draw a line parallel to ST through point R.]

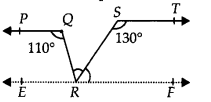
We know that the angles on the same side of transversal is equal to 180°.

So, PQR+QRE = 180°

Or,QRE = 180°-110°

∴ QRE = 70°

Similarly,

RST +SRF = 180°

Or, SRF = 180°- 130°

∴ SRF = 50°

Now, for the linear pairs on the line XY-

QRE+QRS+SRF = 180°

Putting their respective values, we get,

QRS = 180° – 70° – 50°

Hence, QRS = 60°

5. In Fig. 6.32, if AB CD, APQ = 50° and PRD = 127°, find x and y.

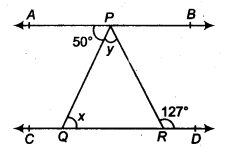
Solution:

From the diagram,

APQ = PQR (Alternate interior angles)

Now, putting the value of APQ = 50° and PQR = x we get,

x = 50°

Also,

APR = PRD (Alternate interior angles)

Or, APR = 127° (As it is given that PRD = 127°)

We know that

APR = APQ+QPR

Now, putting values of QPR = y and APR = 127° we get,

127° = 50°+ y

Or, y = 77°

Thus, the values of x and y are calculated as:

x = 50° and y = 77°

6. In Fig. 6.33, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB CD.

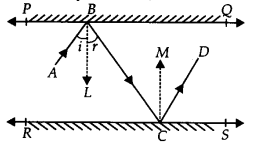
We know that,

Angle of incidence = Angle of reflection (By the law of reflection)

So,

1 = 2 and

3 = 4

We also know that alternate interior angles are equal. Here, BE ⊥ CF and the transversal line BC cuts them at B and C

So, 2 = 3 (As they are alternate interior angles)

Now, 1 +2 = 3 +4

Or, ABC = DCB

So, AB CD alternate interior angles are equal)

Ex 6.3

Question 1.
In figure, sides QP and RQ of ∆PQR are produced to points S and T, respectively. If ∠SPR = 135° and ∠PQT = 110°, find ∠PRQ.

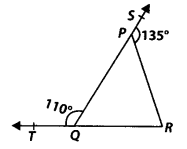
Solution:
We have, ∠TQP + ∠PQR = 180°
[Linear pair]
⇒ 110° + ∠PQR = 180°
⇒ ∠PQR = 180° – 110° = 70°
Since, the side QP of ∆PQR is produced to S.
⇒ ∠PQR + ∠PRQ = 135°
[Exterior angle property of a triangle]
⇒ 70° + ∠PRQ = 135° [∠PQR = 70°]
⇒ ∠PRQ = 135° – 70° ⇒ ∠PRQ = 65°

Question 2.
In figure, ∠X = 62°, ∠XYZ = 54°, if YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ∆XYZ, find ∠OZY and ∠YOZ.

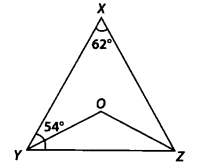
Solution:
In ∆XYZ, we have ∠XYZ + ∠YZX + ∠ZXY = 180°
[Angle sum property of a triangle]
But ∠XYZ = 54° and ∠ZXY = 62°
∴ 54° + ∠YZX + 62° = 180°
⇒ ∠YZX = 180° – 54° – 62° = 64°
YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively.
∴ ∠OYZ = $frac { 1 }{ 2 } angle XYZ$ = $frac { 1 }{ 2 }$ (54°) = 27°
and ∠OZY = $frac { 1 }{ 2 } angle YZX$ = $frac { 1 }{ 2 }$ (64°) = 32°
Now, in ∆OYZ, we have
∠YOZ + ∠OYZ + ∠OZY = 180°
[Angle sum property of a triangle]
⇒ ∠YOZ + 27° + 32° = 180°
⇒ ∠YOZ = 180° -27° – 32° = 121°
Thus, ∠OZY = 32° and ∠YOZ = 121°

Question 3.
In figure, if AB || DE, ∠BAC = 35° and ∠CDE = 539 , find ∠DCE.

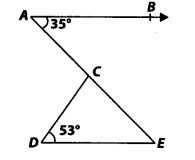
Solution:
AB || DE and AE is a transversal.
So, ∠BAC = ∠AED
[Alternate interior angles]
and ∠BAC = 35° [Given]
∴ ∠AED = 35°
Now, in ∆CDE, we have ∠CDE + ∠DEC + ∠DCE = 180°
{Angle sum property of a triangle]
∴ 53° + 35° + ∠DCE =180°
[∵ ∠DEC = ∠AED = 35° and∠CDE = 53° (Given)]
⇒ ∠DCE = 180° – 53° – 35° = 92°
Thus, ∠DCE = 92°

Question 4.
In figure, if lines PQ and RS intersect at point T, such that ∠ PRT = 40°, ∠ RPT = 95° and ∠TSQ = 75°, find ∠ SQT.

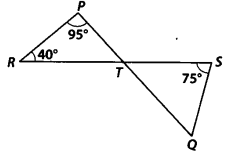
Solution:
In ∆PRT, we have ∠P + ∠R + ∠PTR = 180°
[Angle sum property of a triangle]
⇒ 95° + 40° + ∠PTR =180°
[ ∵ ∠P = 95°, ∠R = 40° (given)]
⇒ ∠PTR = 180° – 95° – 40° = 45°
But PQ and RS intersect at T.
∴ ∠PTR = ∠QTS
[Vertically opposite angles]
∴ ∠QTS = 45° [ ∵ ∠PTR = 45°]
Now, in ∆ TQS, we have ∠TSQ + ∠STQ + ∠SQT = 180°
[Angle sum property of a triangle]
∴ 75° + 45° + ∠SQT = 180° [ ∵ ∠TSQ = 75° and ∠STQ = 45°]
⇒ ∠SQT = 180° – 75° – 45° = 60°
Thus, ∠SQT = 60°

Question 5.
In figure, if PQ ⊥ PS, PQ||SR, ∠SQR = 2S° and ∠QRT = 65°, then find the values of x and y.

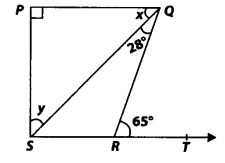
Solution:
In ∆ QRS, the side SR is produced to T.
∴ ∠QRT = ∠RQS + ∠RSQ
[Exterior angle property of a triangle]
But ∠RQS = 28° and ∠QRT = 65°
So, 28° + ∠RSQ = 65°
⇒ ∠RSQ = 65° – 28° = 37°
Since, PQ || SR and QS is a transversal.
∴ ∠PQS = ∠RSQ = 37°
[Alternate interior angles]
⇒ x = 37°
Again, PQ ⊥ PS ⇒ AP = 90°
Now, in ∆PQS,
we have ∠P + ∠PQS + ∠PSQ = 180°
[Angle sum property of a triangle]
⇒ 90° + 37° + y = 180°
⇒ y = 180° – 90° – 37° = 53°
Thus, x = 37° and y = 53°

Question 6.
In figure, the side QR of ∆PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that

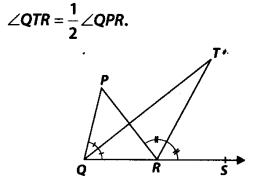
Solution:
In ∆PQR, side QR is produced to S, so by exterior angle property,
∠PRS = ∠P + ∠PQR
⇒ $frac { 1 }{ 2 }$ ∠PRS = $frac { 1 }{ 2 }$ ∠P + $frac { 1 }{ 2 }$ ∠PQR
⇒ ∠TRS = $frac { 1 }{ 2 }$ ∠P + ∠TQR …(1)
[∵ QT and RT are bisectors of ∠PQR and ∠PRS respectively.]
Now, in ∆QRT, we have
∠TRS = ∠TQR + ∠T …(2)
[Exterior angle property of a triangle]
From (1) and (2),
we have ∠TQR + $frac { 1 }{ 2 }$ ∠P = ∠TQR + ∠T
⇒ $frac { 1 }{ 2 }$ ∠P = ∠T
⇒ $frac { 1 }{ 2 }$ ∠QPR = ∠QTR or ∠QTR = $frac { 1 }{ 2 }$ ∠QPR