Ex 7.1
Question 1.
Find the distance between the following pairs of points:
(i) (2, 3), (4, 1)
(ii) (-5, 7), (-1, 3)
(iii) (a, b), (-a, -b)
Solution:
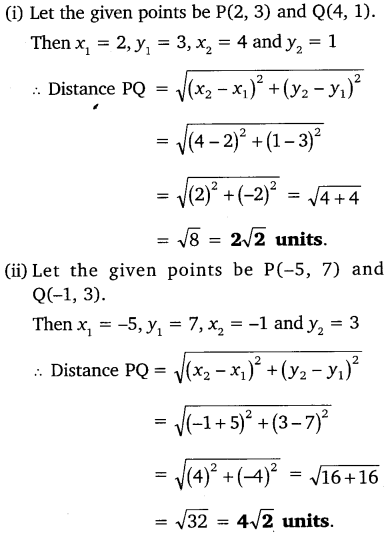
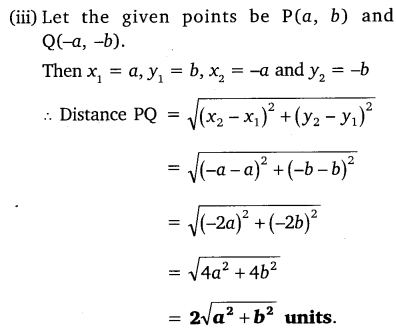
Question 2.
Find the distance between the points (0, 0) and (36, 15).
Solution:
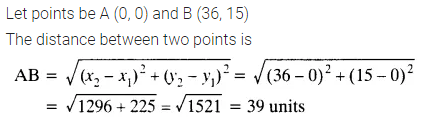
Question 3.
Determine if the points (1, 5), (2, 3) and (-2, -11) are collinear.
Solution:
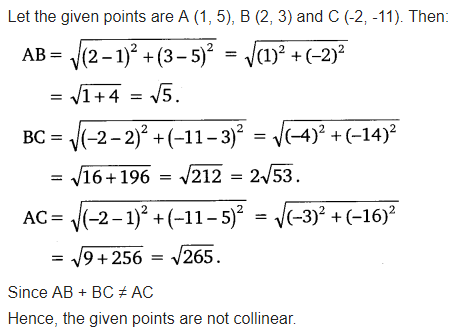
Question 4.
Check whether (5, -2), (6, 4) and (7, -2) are the vertices of an isosceles triangle.
Solution:
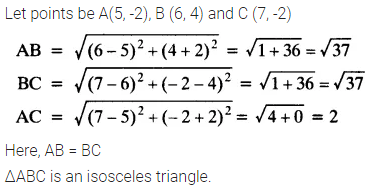
Question 5.
In a classroom, 4 friends are seated at the points A, B, C and D as shown in the given figure. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using distance formula, find which of them is correct.
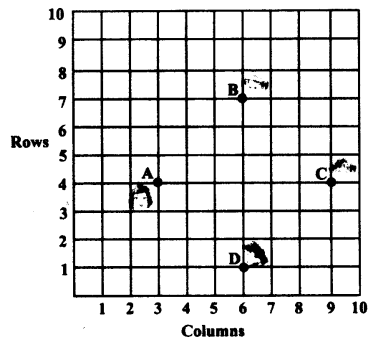
Solution:
Question 6.
Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer.
(i) (-1, -2), (1, 0), (-1, 2), (-3, 0)
(ii) (-3, 5), (3, 1), (0, 3), (-1, -4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
Solution:
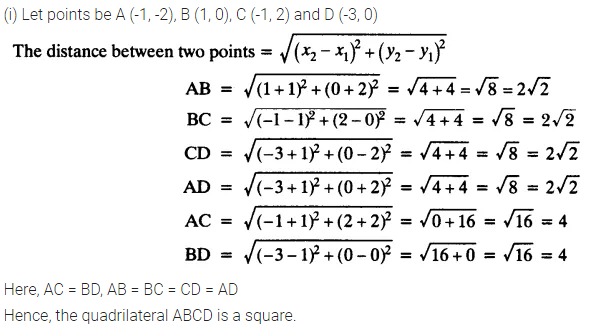
Question 7.
Find the point on the x-axis which is equidistant from (2, -5) and (-2, 9).
Solution:
Question 8.
Find the values of y for which the distance between the points P (2, -3) and Q (10, y) is 10 units.
Solution:
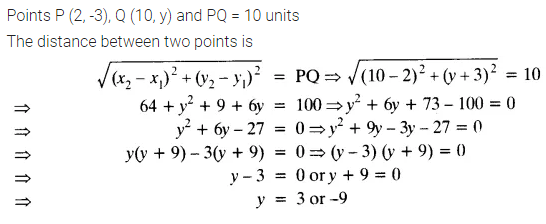
Question 9.
If Q (0, 1) is equidistant from P (5, -3), and R (x, 6), find the values of x. Also, find the distances QR and PR.
Solution:
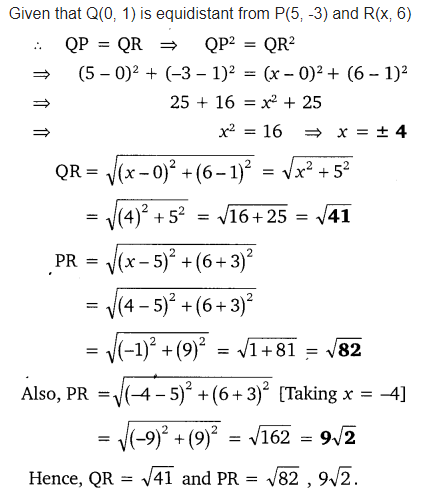
Question 10.
Find a relation between x and y such that the point (x, y) is equidistant from the points (3, 6) and (-3, 4).
Solution:
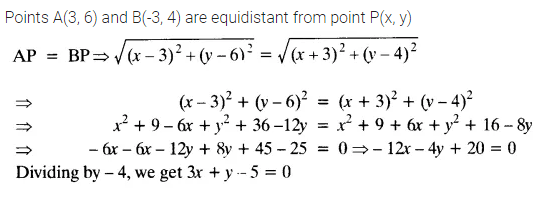
Ex 7.2
Question 1.
Find the coordinates of the point which divides the join of (-1, 7) and (4, -3) in the ratio 2 : 3.
Solution:
Question 2.
Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).
Solution:
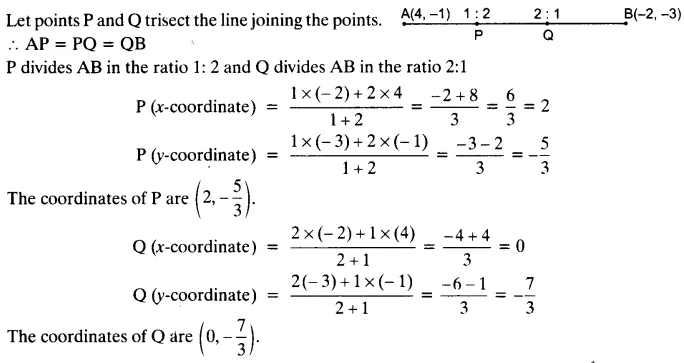
Question 3.
To conduct Sports Day activities, in your rectangular shaped school ground ABCD, lines have been drawn with chalk powder at a distance of 1 m each. 100 flower pots have been placed at a distance of 1 m from each other along AD, as shown in given
figure below. Niharika runs 
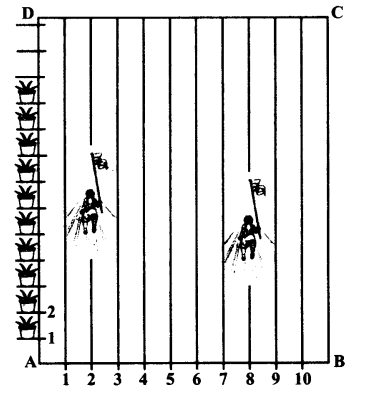
Solution:
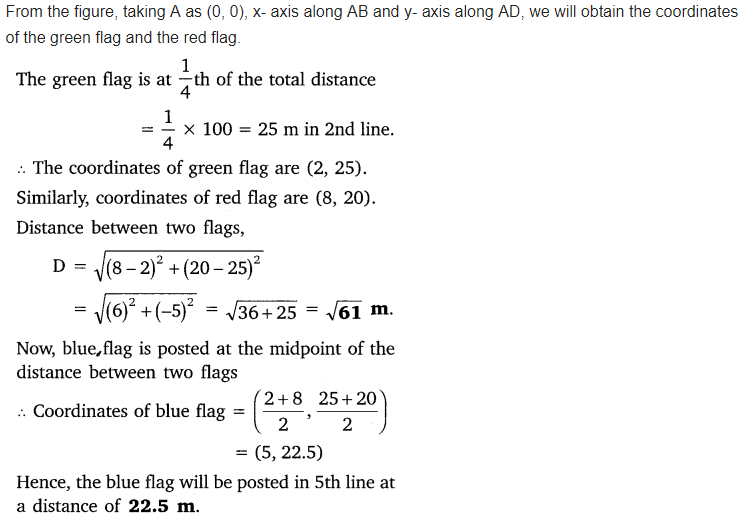
Question 4.
Find the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by (-1, 6).
Solution:
Question 5.
Find the ratio in which line segment joining A (1, -5) and B (-4, 5) is divided by the x-axis. Also, find the coordinates of the point of division.
Solution:
Question 6.
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Solution:
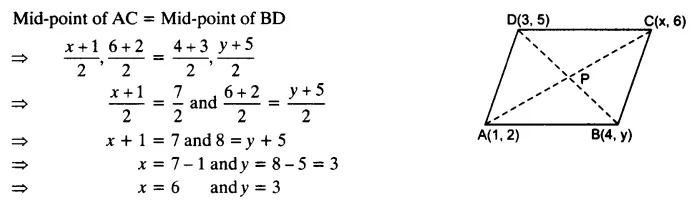
Question 7.
Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).
Solution:
Question 8.
If A and B are (-2, -2) and (2, -4), respectively, find the coordinates of P such that AP =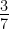 
AB and P lies on the line segment AB.
Solution:
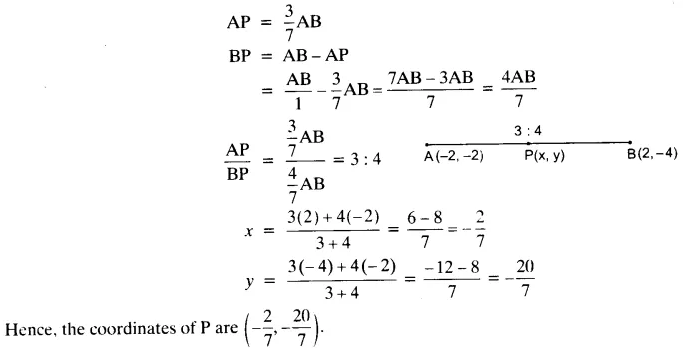
Question 9.
Find the coordinates of the points which divide the line segment joining A (-2, 2) and B (2, 8) into four equal parts.
Solution:
Question 10.
Find the area of a rhombus if its vertices are (3, 0), (4, 5), (-1, 4) and (-2, -1) taken in order.
[Hint: Area of a rhombus =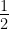 
(product of its diagonals)]
Solution:
Ex 7.3
1.Find the area of the triangle whose vertices are:
(i) (2, 3), (-1, 0), (2, -4)
(ii) (-5, -1), (3, -5), (5, 2)
Solution:
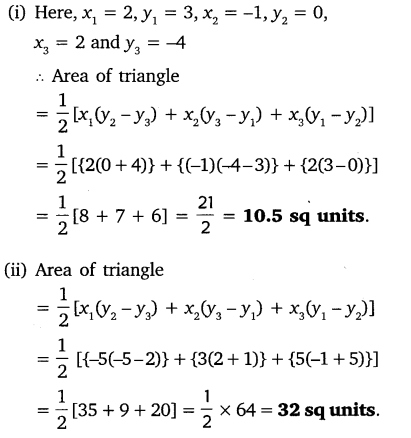
2. In each of the following find the value of ‘k’ for which the points are collinear.
(i) (7, -2), (5, 1), (3, k)
(ii) (8, 1), (k, -4), (2, -5)
Solution:
3. Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
Solution:
4. Find the area of the quadrilateral whose vertices, taken in order, are (-4, -2), (-3, -5), (3, -2) and (2, 3).
Solution:
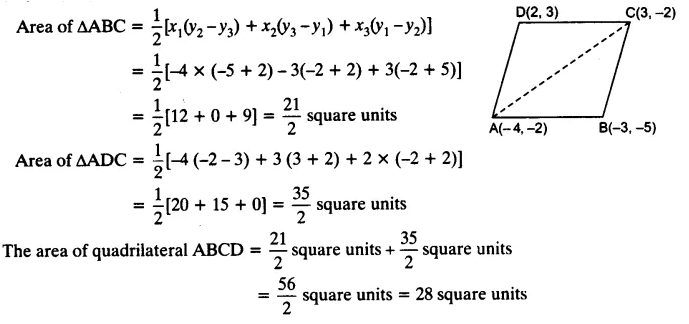
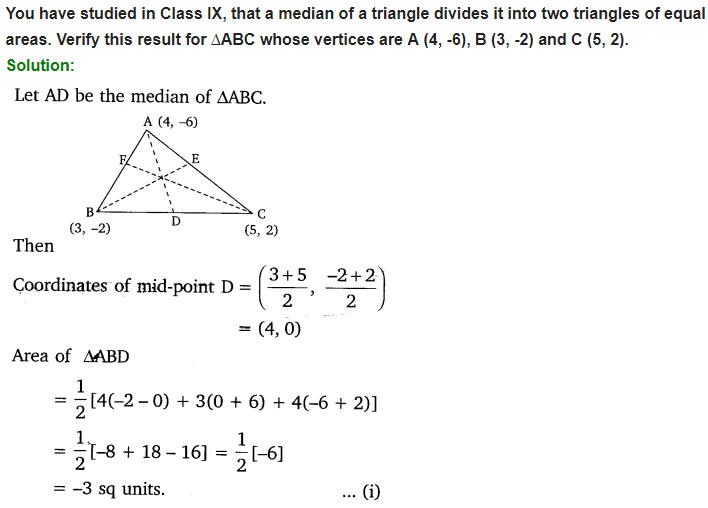
5. You have studied in Class IX, that a median of a triangle divides it into two triangles of equal areas. Verify this result for ∆ABC whose vertices are A (4, -6), B (3, -2) and C (5, 2).
Solution:
