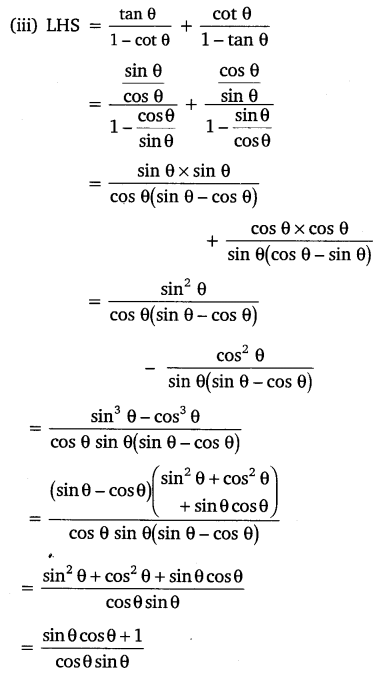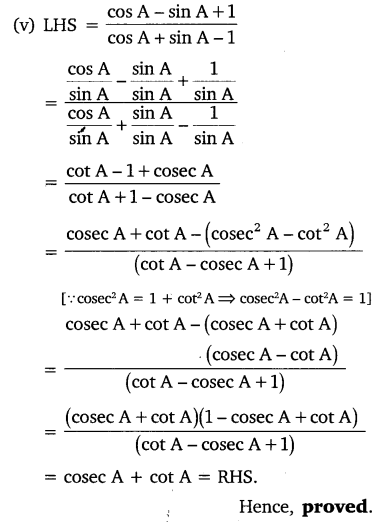Question 1.
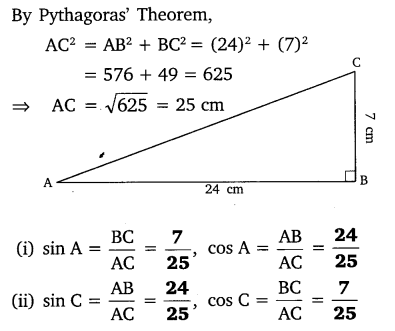
In ∆ABC right angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) sin A, cos A
(ii) sin C, cos C
Solution:
Question 2.
In given figure, find tan P – cot R.
Solution:
Question 3.
If sin A = 
, calculate cos A and tan A.
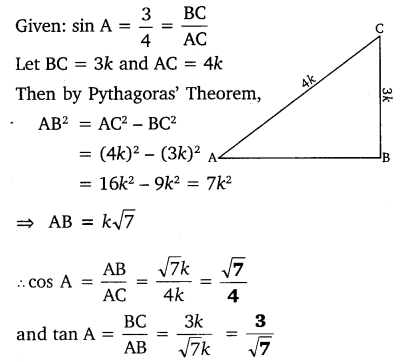
Question 4.
Given 15 cot A = 8, find sin A and sec A.
Solution:
Question 5.
Given sec θ =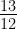 
, calculate all other trigonometric ratios.
Solution:
Let us assume a right angled triangle ABC, right angled at B
sec θ =13/12 = Hypotenuse/Adjacent side = AC/AB
According to the Pythagoras theorem,
AC2=AB2 + BC2
Substitute the value of AB and AC
(13k)2= (12k)2 + BC2
169k2= 144k2 + BC2
169k2= 144k2 + BC2
BC2 = 169k2 – 144k2
BC2= 25k2
Therefore, BC = 5k
Now, substitute the corresponding values in all other trigonometric ratios
So,
Sin θ = Opposite Side/Hypotenuse = BC/AC = 5/13
Cos θ = Adjacent Side/Hypotenuse = AB/AC = 12/13
tan θ = Opposite Side/Adjacent Side = BC/AB = 5/12
Cosec θ = Hypotenuse/Opposite Side = AC/BC = 13/5
cot θ = Adjacent Side/Opposite Side = AB/BC = 12/5
Question 6.
If ∠A and ∠B are acute angles such that cos A = cos B, then show that ∠A = ∠B.
Solution:
Question 7.
If cot θ = 7/8, evaluate :
(i) (1 + sin θ)(1 – sin θ)/(1+cos θ)(1-cos θ)
(ii) cot2 θ
Solution:
Let us assume a △ABC in which ∠B = 90° and ∠C = θ
Given:
cot θ = BC/AB = 7/8
Let BC = 7k and AB = 8k, where k is a positive real number
According to Pythagoras theorem in △ABC we get.
AC2 = AB2+BC2
AC2 = (8k)2+(7k)2
AC2 = 64k2+49k2
AC2 = 113k2
AC = √113 k
According to the sine and cos function ratios, it is written as
sin θ = AB/AC = Opposite Side/Hypotenuse = 8k/√113 k = 8/√113 and
cos θ = Adjacent Side/Hypotenuse = BC/AC = 7k/√113 k = 7/√113
Now apply the values of sin function and cos function:
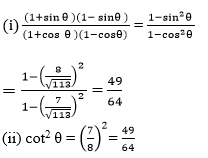
Question 8.
If 3 cot A = 4, check whether 
= cos² A – sin² A or not.
Solution:
Question 9.
In triangle ABC, right-angled at B, if tan A = 1/√3 find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C
Solution:
Question 10.
In ∆ PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P
Solution:
In a given triangle PQR, right angled at Q, the following measures are
PQ = 5 cm
PR + QR = 25 cm
Now let us assume, QR = x
PR = 25-QR
PR = 25- x
According to the Pythagorean Theorem,
PR2 = PQ2 + QR2
Substitute the value of PR as x
(25- x) 2 = 52 + x2
252 + x2 – 50x = 25 + x2
625 + x2-50x -25 – x2 = 0
-50x = -600
x= -600/-50
x = 12 = QR
Now, find the value of PR
PR = 25- QR
Substitute the value of QR
PR = 25-12
PR = 13
Now, substitute the value to the given problem
(1) sin p = Opposite Side/Hypotenuse = QR/PR = 12/13
(2) Cos p = Adjacent Side/Hypotenuse = PQ/PR = 5/13
(3) tan p =Opposite Side/Adjacent side = QR/PQ = 12/5
11. State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = 12/5 for some value of angle A.
(iii)cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = 4/3 for some angle θ.
Solution:
(i) The value of tan A is always less than 1.
Answer: False
Proof: In ΔMNC in which ∠N = 90∘,
MN = 3, NC = 4 and MC = 5
Value of tan M = 4/3 which is greater than.
The triangle can be formed with sides equal to 3, 4 and hypotenuse = 5 as it will follow the Pythagoras theorem.
MC2=MN2+NC2
52=32+42
25=9+16
25 = 25
(ii) sec A = 12/5 for some value of angle A
Answer: True
Justification: Let a ΔMNC in which ∠N = 90º,
MC=12k and MB=5k, where k is a positive real number.
By Pythagoras theorem we get,
MC2=MN2+NC2
(12k)2=(5k)2+NC2
NC2+25k2=144k2
NC2=119k2
Such a triangle is possible as it will follow the Pythagoras theorem.
(iii) cos A is the abbreviation used for the cosecant of angle A.
Answer: False
Justification: Abbreviation used for cosecant of angle M is cosec M. cos M is the abbreviation used for cosine of angle M.
(iv) cot A is the product of cot and A.
Answer: False
Justification: cot M is not the product of cot and M. It is the cotangent of ∠M.
(v) sin θ = 4/3 for some angle θ.
Answer: False
Justification: sin θ = Height/Hypotenuse
We know that in a right angled triangle, Hypotenuse is the longest side.
∴ sin θ will always less than 1 and it can never be 4/3 for any value of θ.
Ex 8.2
Question 1.
Evaluate the following:
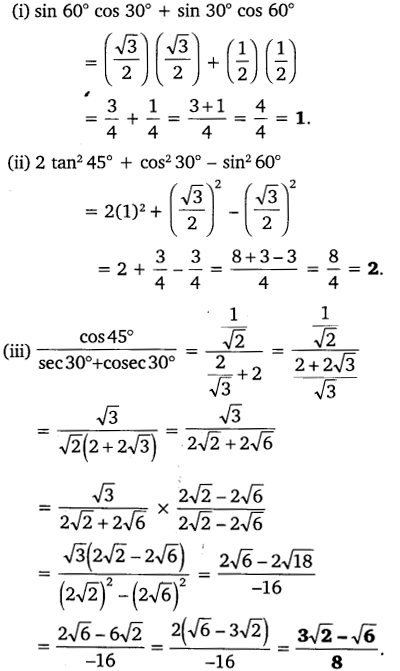
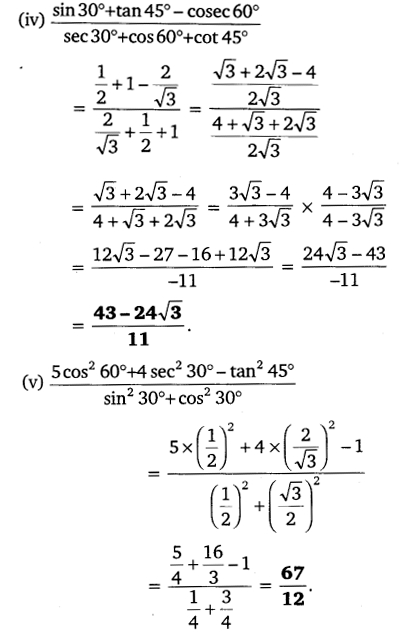
Question 2.
Choose the correct option and justify your choice:
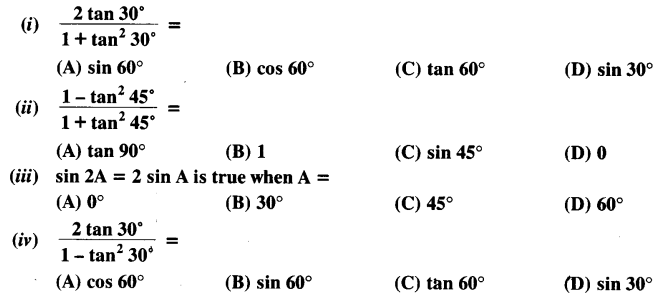
Question 3.
If tan (A + B) = √3 and tan (A – B) = 1/√3 ,0° < A + B ≤ 90°; A > B, find A and B.
Solution:
tan (A + B) = √3
Since √3 = tan 60°
Now substitute the degree value
⇒ tan (A + B) = tan 60°
(A + B) = 60° … (i)
The above equation is assumed as equation (i)
tan (A – B) = 1/√3
Since 1/√3 = tan 30°
Now substitute the degree value
⇒ tan (A – B) = tan 30°
(A – B) = 30° … equation (ii)
Now add the equation (i) and (ii), we get
A + B + A – B = 60° + 30°
Cancel the terms B
2A = 90°
A= 45°
Now, substitute the value of A in equation (i) to find the value of B
45° + B = 60°
B = 60° – 45°
B = 15°
Therefore A = 45° and B = 15°
Question 4.
State whether the following statements are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
(ii) The value of sin θ increases as θ increases.
(iii) The value of cos θ increases as θ increases.
(iv) sin θ = cos θ for all values of θ.
(v) cot A is not defined for A = 0°.
Solution:
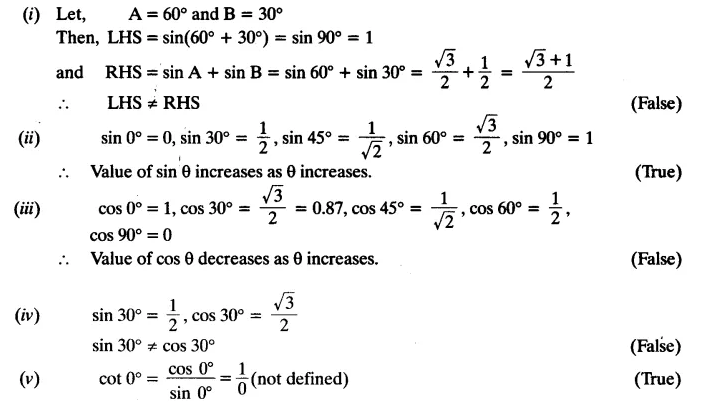
Ex 8.3
Question 1.
Evaluate:
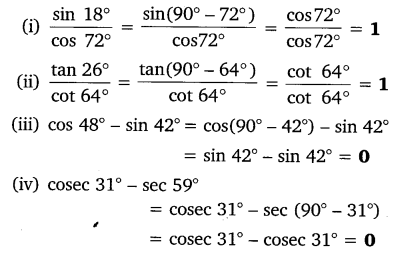
Question 2.
Show that:
(i) tan 48° tan 23° tan 42° tan 67° = 1
(ii) cos 38° cos 52° – sin 38° sin 52° = 0
Solution:
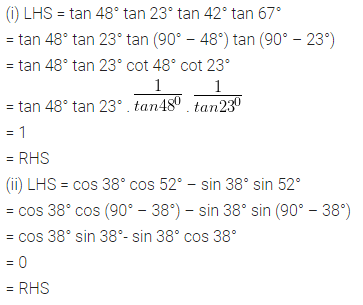
Question 3.
If tan 2A = cot (A – 18°), where 2A is an acute angle, find the value of A.
Solution:
tan 2A = cot (A- 18°)
We know that tan 2A = cot (90° – 2A)
Substitute the above equation in the given problem
⇒ cot (90° – 2A) = cot (A -18°)
Now, equate the angles,
⇒ 90° – 2A = A- 18° ⇒ 108° = 3A
A = 108° / 3
Therefore, the value of A = 36°
Question 4.
If tan A = cot B, prove that A + B = 90°.
Solution:
tan A = cot B
We know that cot B = tan (90° – B)
To prove A + B = 90°, substitute the above equation in the given problem
tan A = tan (90° – B)
A = 90° – B
A + B = 90°
Question 5.
If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.
Solution:
sec 4A = cosec (A – 20°)
We know that sec 4A = cosec (90° – 4A)
To find the value of A, substitute the above equation in the given problem
cosec (90° – 4A) = cosec (A – 20°)
Now, equate the angles
90° – 4A= A- 20°
110° = 5A
A = 110°/ 5 = 22°
Therefore, the value of A = 22°
Question 6.
If A, B and C are interior angles of a triangle ABC, then show that
sin (B+C/2) = cos A/2
Solution:
We know that, for a given triangle, sum of all the interior angles of a triangle is equal to 180°
A + B + C = 180° ….(1)
To find the value of (B+ C)/2, simplify the equation (1)
⇒ B + C = 180° – A
⇒ (B+C)/2 = (180°-A)/2
⇒ (B+C)/2 = (90°-A/2)
Now, multiply both sides by sin functions, we get
⇒ sin (B+C)/2 = sin (90°-A/2)
Since sin (90°-A/2) = = cos A/2, the above equation is equal to
sin (B+C)/2 = cos A/2
Question 7.
Express sin 67° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
Solution:
Given:
sin 67° + cos 75°
In term of sin as cos function and cos as sin function, it can be written as follows
sin 67° = sin (90° – 23°)
cos 75° = cos (90° – 15°)
= sin (90° – 23°) + cos (90° – 15°)
Now, simplify the above equation
= cos 23° + sin 15°
Therefore, sin 67° + cos 75° is also expressed as cos 23° + sin 15°
Ex 8.4
Question 1.
Express the trigonometric ratios sin A, sec A and tan A in terms of cot A.
Solution:
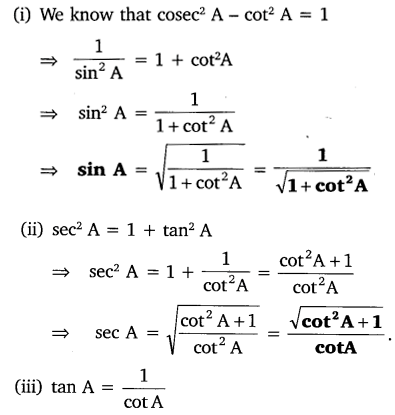
Question 2.
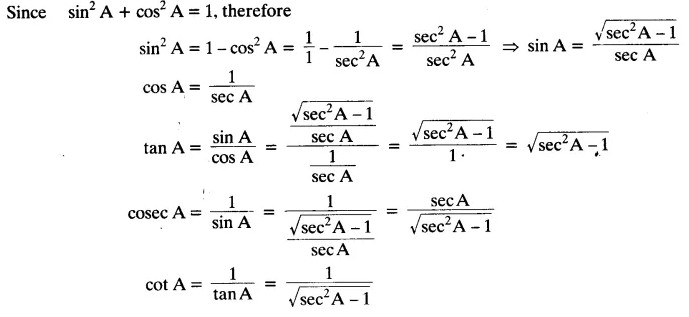
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:
Question 3.
Evaluate:
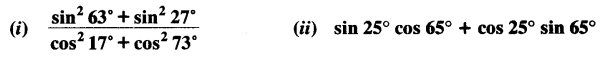
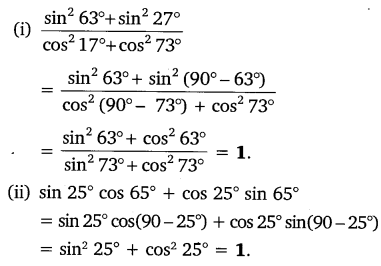
Question 4.
Choose the correct option. Justify your choice.
(i) 9 sec2A – 9 tan2A =
(A) 1 (B) 9 (C) 8 (D) 0
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ)
(A) 0 (B) 1 (C) 2 (D) – 1
(iii) (sec A + tan A) (1 – sin A) =
(A) sec A (B) sin A (C) cosec A (D) cos A
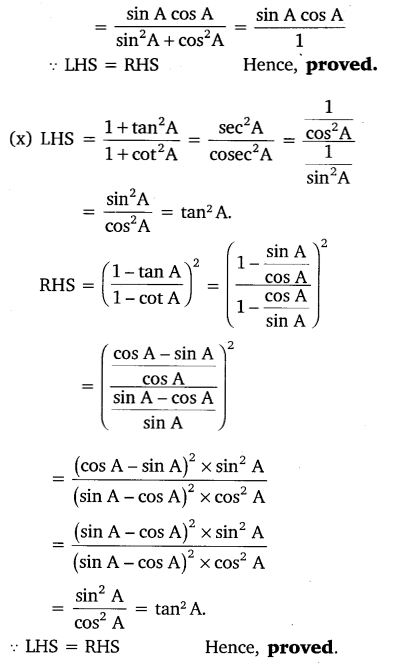
(iv) 1+tan2A/1+cot2A =
(A) sec2 A (B) -1 (C) cot2A (D) tan2A
Solution:
Question 5.
Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
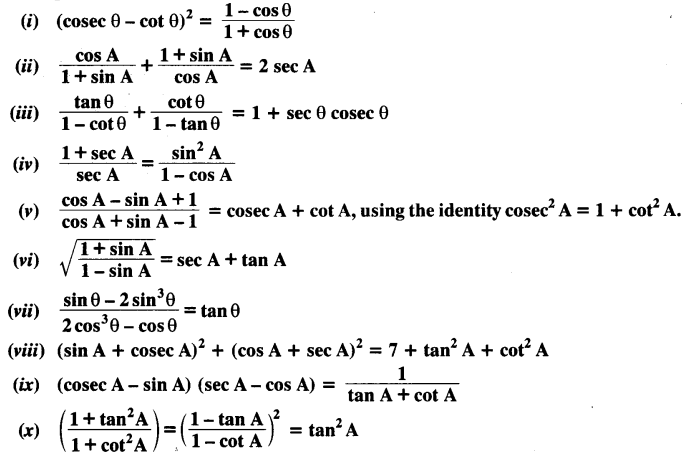
Solution:
