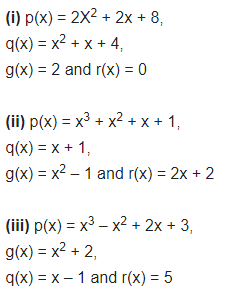Ex 2.1
Question 1:
The graphs of y = p(x) are given below for some polynomials p(x). Find the number of zeroes of p(x) in each case.

Solution:
Ex 2.2
Question 1.
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and their coefficients:
(i) x2 – 2x – 8
x2 – 4x +2x – 8
x (x-4) 2 (x-4)
(x-4)(x+2)
x-4 = 0
x = 4
x+2 = 0
x = -2
So zeroes are 4 and -2
Verifications:
x2 – 4x +2x – 8
sum of zeroes = -b/a
4+(-2) = -(-2)/1
4-2 = 2/1
2 =2 verify
product of zeroes = c/a
4 x -2 = -8/1
-8 = -8 verify
(ii) 4s2 – 4s + 1
4s2 – 2s - 2s + 1
2s(2s-1) -1 (2s-1)
(2s-1)(2s-1)
2s-1 = 0
2s = 1
s = 1/2
so, zeroes are 1/2 , 1/2
Verifications:
4s2 – 4s + 1
sum of zeroes = -b/a
1/2 + 1/2 = -(-4)/4
2/2 = 4/4
1 =1 verify
product of zeroes = c/a
1/2 x 1/2 = 1/4
1/4 = 1/4 verify
(iii) 6x2 – 3 – 7x
first we write in order
6x2 - 7x - 3
6x2 - 9x + 2x -3
3x(2x - 3) +1(2x -3)
(2x - 3)(3x + 1)
2x - 3 = 0
2x = 3
x = 3/2
3x + 1 = 0
3x = -1
x = -1/3
so, zeroes are 3/2 and -1/3
Verifications:
6x2 - 7x - 3
sum of zeroes = -b/a
3/2 +(- 1/3) = -(-7)/6
3/2 - 1/3 = 7/6
7/6 = 7/6 verify
product of zeroes = c/a
3/2 x -1/3 = -3/6
-3/6 = -3/6 verify
(iv) 4u2 + 8u
4u is common so,
4u ( u + 2)
4u = 0
u = 0
u + 2 = 0
u = -2
Verifications:
4u2 + 8u
sum of zeroes = -b/a
0 + ( -2) = - 8/4
-2 = -2 verify
product of zeroes = c/a
0 x -2 = 0/4
0 = 0 verify
(v) t2 – 15
t2 – ( )2 . :
)2 . :  X
X  = 15
= 15
From Identitity A2 - B 2 = ( A + B ) (A - B)
(t +  ) (t -
) (t -  )
)
S0, zeroes are  and -
and - 
Verifications:
sum of zeroes = -b/a
 -
-  = 0 = - 0/1
= 0 = - 0/1
product of zeroes = c/a
 x -
x -  = - 15 = -15/1 verify
= - 15 = -15/1 verify
(vi) 3x2 – x – 4
3x2 + 3x - 4 x – 4
3x ( x+1) -4 (x+1)
(3x - 4) ( x + 1)
(3x - 4) = 0
x = 4/3
( x + 1) = 0
x = -1
S0, zeroes are 4/3 and -1
Verifications:
sum of zeroes = -b/a
4/3 + (-1) = -(-1)/3
4/3 - 1 = 1/3 = 1/3
product of zeroes = c/a
4/3 x -1 = -4/3 verify
Question 2.
Find a quadratic polynomial each with the given numbers as the sum and product of zeroes respectively:


Ex 2.3
Question 1.
Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
(i) p(x) = x3 – 3x2 + 5x – 3, g(x) = x2 – 2
(ii) p(x) = x4 – 3x2 + 4x + 5, g(x) = x2 + 1 – x
(iii) p(x) = x4– 5x + 6, g(x) = 2 – x2
Solution:

Question 2.
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial.
(i) t2 – 3, 2t4 + 3t3 – 2t2– 9t – 12
(ii) x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
(iii) x2 + 3x + 1, x5 – 4x3 + x2 + 3x + 1
Solution:

Question 3.
Obtain all other zeroes of 3x4 + 6x3 – 2x2 – 10x – 5, if two of its zeroes are


Question 5.
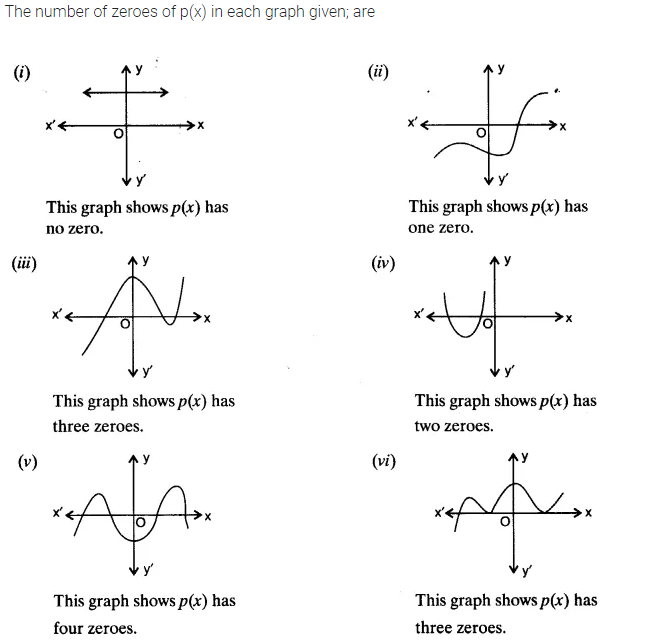
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and:
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solution: