NCERT Solutions Class 7 Maths Ch15 Visualising Solid Shapes
Question 1.
Identify the nets which can be used to make cubes (Cut out copies of the nets and try it):
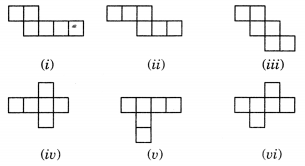
Solution:
Fig. (ii), (iii), (iv) and (vi) can be used to make cubes.
Question 2.
Dice are cubes with dots on each face. Opposite faces of a die always have a total of seven dots on them.
Here are two nets to make dice (cubes); the number inserted in each square indicate the number of dots in that box.
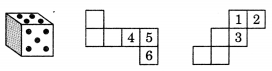
Insert suitable number in the blanks, remembering that the number on the opposite faces should total to 7.
Solution:
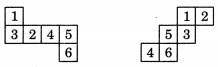
Question 3.
Can this be a net for a die? Explain your answer.
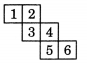
Solution:
If one pair of opposite faces will have 1 and 4 on them, then their total does not come 7.
If we take 3 and 6 on the opposite faces of the die, then the total does not come 7.
Hence, this cannot be for a die.
Question 4.
Here is an incomplete net for making a cube. Complete it in atleast two different ways. Remember that a cube has six faces. How many are there in the net here? (Give two separate diagrams. If you like, you may use a squared sheet for easy manipulation).
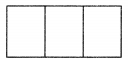
Solution:
There are three faces in the given net.
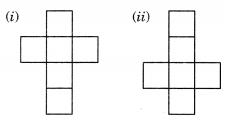
Question 5.
Match the nets with appropriate solids:
Solution:
(a) (ii)
(b) (iii)
(c) (iv)
(d) (i)
Ex 15.2
Question 1.
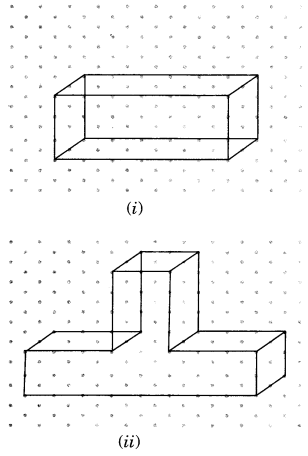
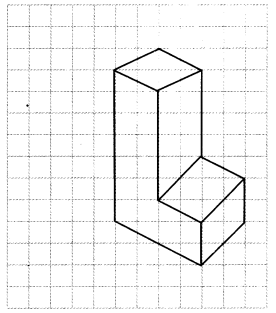
Use isometric dot paper and make an isometric sketch for each one of the given shapes:

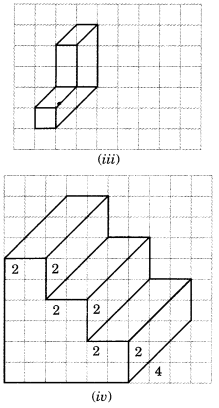
Solution:
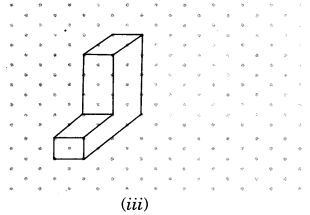
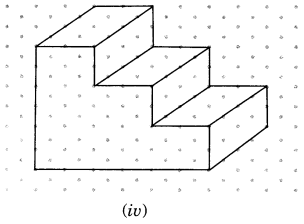
Question 2.
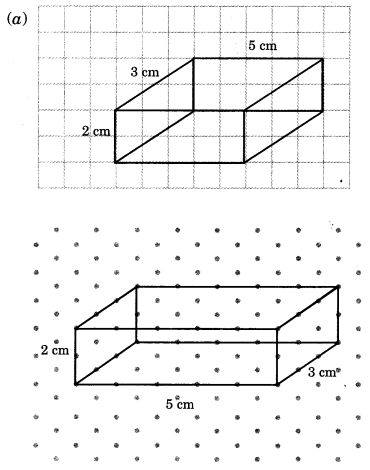
The dimensions of a cuboid are 5 cm, 3 cm and 2 cm. Draw three different isometric sketches of this cuboid.
Solution:
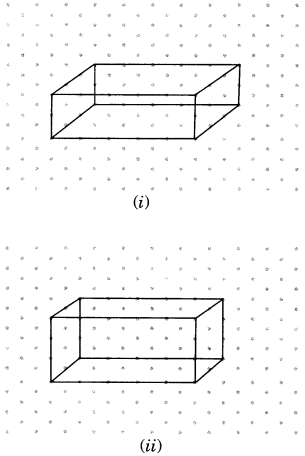
Question 3.
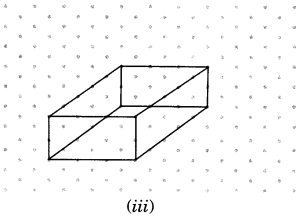
Three cubes with 2 cm edge are placed side by side to form a cuboid. Sketch an oblique or isometric sketch of this cuboid.
Solution:
In the given figure, we have an isometric sketch of a cuboid formed by placing three cubes each of 2 cm edge side by side.
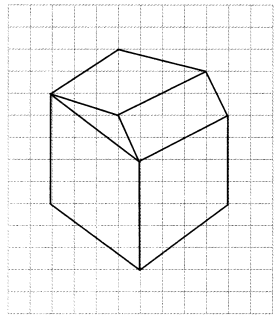
Question 4.
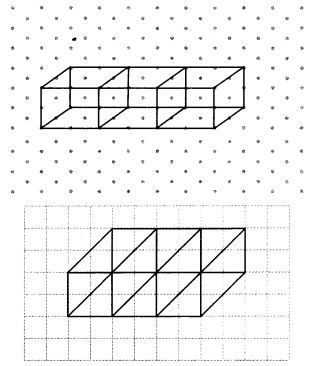
Make an oblique sketch for each one of the given isometric shapes:

Solution:
Question 5.
Give (i) an oblique sketch and (ii) an isometric sketch for each of the following:
(а) A cuboid of dimensions 5 cm, 3 cm and 2 cm. (Is your sketch unique?)
(b) A cube with an edge 4 cm long.
An isometric sheet is attached at the end of the book. You could try to make on it some cubes or cuboids of dimensions specified by your friend.
Solution:
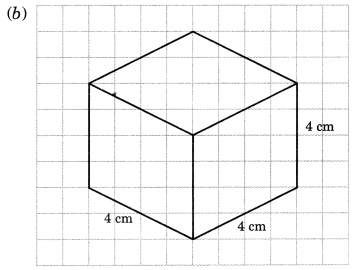

No, this sketch is not unique.
Ex 15.3
Question 1.
What cross-sections do you get when you give a
(i) vertical cut
(ii) horizontal cut to the following solids?
(a) A brick
(b) A round apple
(c) A die
(d) A circular pipe
(e) An ice cream cone.
Solution:
| Solids | Shape of cross-section of vertical cut | Shape of crosssection for horizontal cut |
| (a) A brick | Rectangle | Rectangle |
| (b) A round apple | Circle | Circle |
| (c) A die | Square | Square |
| (d) A circular pipe | Circle | Rectangle |
| (e) An ice cream apple | Triangle | Circle |
Ex 15.4
Question 1.
A bulb is kept burning just right above the following solids. Name the shape of the shadows obtained in each case. Attempt to give a rough sketch of the shadow. (You may try to experiment first and then answer these questions).

Solution:
When the light falls just above the solids.
(i) A ball; the shadow looks like a circle.
(ii) A cylindrical pipe; the shadow looks like nearly rectangular.
(iii) A book; the shadow looks like nearly rectangular.
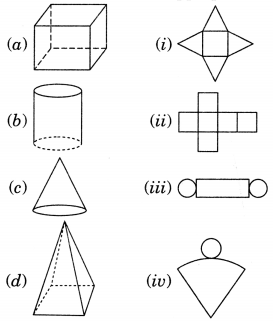
Question 2.
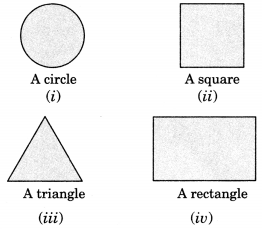
Here are the shadows of some 3-D objects, when seen under the lamp of an overhead projector. Identify the solid(s) that match each shadow. (There may be multiple answers for these!)
Solution:
(i) The given shadow corresponds to a sphere.
(ii) The given shadow corresponds to a cube.
(iii) The given shadow corresponds to a pyramid.
(iv) The given shadow corresponds to a cuboid or a cylinder.
Question 3.
Examine if the following are true statements:
(i) The cube can cast a shadow in the shape of a rectangle.
(ii) The cube can cast a shadow in the shape of a hexagon.
Solution:
(i) The given statement is true.
(ii) The given statement is false.


