NCERT Solutions class 9 Maths Ch- 1 Number Systems

NCERT Solutions Class 9 Maths Chapter 1 Number Systems

Ex 1.1

1. Is zero a rational number? Can you write it in the form p/q where p and q are integers and q ≠ 0?

Solution:

We know that, a number is said to be rational if it can be written in the form p/q , where p and q are integers and q ≠ 0.

Taking the case of ‘0’,

Zero can be written in the form 0/1, 0/2, 0/3 … as well as , 0/1, 0/2, 0/3 ..

Since it satisfies the necessary condition, we can conclude that 0 can be written in the p/q form, where q can either be positive or negative number.

Hence, 0 is a rational number.

2. Find six rational numbers between 3 and 4.

Solution:

There are infinite rational numbers between 3 and 4.

As we have to find 6 rational numbers between 3 and 4, we will multiply both the numbers, 3 and 4, with 6+1 = 7 (or any number greater than 6)

i.e., 3 × (7/7) = 21/7

and, 4 × (7/7) = 28/7. The numbers in between 21/7 and 28/7 will be rational and will fall between 3 and 4.

Hence, 22/7, 23/7, 24/7, 25/7, 26/7, 27/7 are the 6 rational numbers between 3 and 4.

3. Find five rational numbers between 3/5 and 4/5.

Solution:

There are infinite rational numbers between 3/5 and 4/5.

To find out 5 rational numbers between 3/5 and 4/5, we will multiply both the numbers 3/5 and 4/5

with 5+1=6 (or any number greater than 5)

i.e., (3/5) × (6/6) = 18/30

and, (4/5) × (6/6) = 24/30

The numbers in between18/30 and 24/30 will be rational and will fall between 3/5 and 4/5.

Hence,19/30, 20/30, 21/30, 22/30, 23/30 are the 5 rational numbers between 3/5 and 4/5

4. State whether the following statements are true or false. Give reasons for your answers.

(i) Every natural number is a whole number.

Solution:

True

Natural numbers- Numbers starting from 1 to infinity (without fractions or decimals)

i.e., Natural numbers= 1,2,3,4…

Whole numbers- Numbers starting from 0 to infinity (without fractions or decimals)

i.e., Whole numbers= 0,1,2,3…

Or, we can say that whole numbers have all the elements of natural numbers and zero.

Every natural number is a whole number; however, every whole number is not a natural number.

(ii) Every integer is a whole number.

Solution:

False

Integers- Integers are set of numbers that contain positive, negative and 0; excluding fractional and decimal numbers.

i.e., integers= {…-4,-3,-2,-1,0,1,2,3,4…}

Whole numbers- Numbers starting from 0 to infinity (without fractions or decimals)

i.e., Whole numbers= 0,1,2,3….

Hence, we can say that integers include whole numbers as well as negative numbers.

Every whole number is an integer; however, every integer is not a whole number.

(iii) Every rational number is a whole number.

Solution:

False

Rational numbers- All numbers in the form p/q, where p and q are integers and q≠0.

i.e., Rational numbers = 0, 19/30 , 2, 9/-3, -12/7…

Whole numbers- Numbers starting from 0 to infinity (without fractions or decimals)

i.e., Whole numbers= 0,1,2,3….

Hence, we can say that integers include whole numbers as well as negative numbers.

All whole numbers are rational, however, all rational numbers are not whole numbers.

 

Ex 1.2

Question 1.
State whether the following statements are true or false. Justify your answers.
(i) Every irrational number is a real number.
(ii) Every point on the number line is of the form √m , where m is a natural number.
(iii) Every real number is an irrational number.
Solution:
(i) True
Because all rational numbers and all irrational numbers form the group (collection) of real numbers.
(ii) False
Because negative numbers cannot be the square root of any natural number.
(iii) False
Because rational numbers are also a part of real numbers.

Question 2.
Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.
Solution:
No, if we take a positive integer, say 9, its square root is 3, which is a rational number.

Question 3.
Show how √5 can be represented on the number line.
Solution:
Draw a number line and take point O and A on it such that OA = 1 unit. Draw BA ⊥ OA as BA = 1 unit. Join OB = √2 units.
Now draw BB₁ ⊥ OB such that BB₁ =1 unit. Join OB₁ = √3 units.
Next, draw B₁B₂⊥ OB₁such that B₁B₂ = 1 unit.
Join OB₂ = units.
Again draw B₂B₃ ⊥OB₂ such that B₂B₃ = 1 unit.
Join OB₃ = √5 units.

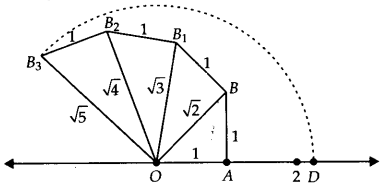
Take O as centre and OB₃ as radius, draw an arc which cuts the number line at D.
Point D
represents √5 on the number line.

 

 Ex 1.3

Question 1.
Write the following in decimal form and say what kind of decimal expansion each has

Solution:
(i) We have,  = 0.36
Thus, the decimal expansion of  is terminating.

(ii) Dividing 1 by 11, we have

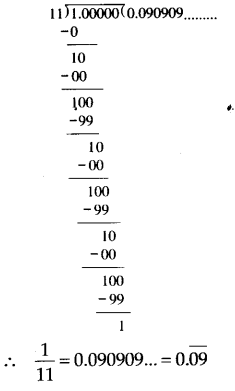
Thus, the decimal expansion of 1/11 is non-terminating repeating.

 

(iii)4

Dividing 33 by 8, we get

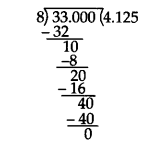
Thus, it is terminating.

 

(iv) Dividing 3 by 13, we get

 

Thus, it is non-terminating repeating.

 

(v) Dividing 2 by 11, we get

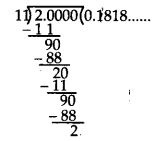
Thus, it is non-terminating repeating.

 

(vi) Dividing 329 by 400, we get

Thus, it is terminating repeating.

2. You know that 1/7 = 0.142857. Can you predict what the decimal expansions of 2/7, 3/7, 4/7, 5/7, 6/7 are, without actually doing the long division? If so, how?

[Hint: Study the remainders while finding the value of 1/7 carefully.]

Solution:

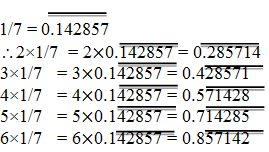
3. Express the following in the form p/q, where p and q are integers and q 0

(i)

Solution:

Assume that  x = 0.666…

Then,10x = 6.666…

10x = 6 + x

9x = 6

x = 2/3

(ii) 0.4

Solution:

$0.4777....$

Assume that x = 0.777…

Then, 10x = 7.777…

10x = 7 + x

x = 7/9

(iii)  0.

Solution:

Assume that  x = 0.001001…

Then, 1000x = 1.001001…

1000x = 1 + x

999x = 1

x = 1/999

4. Express 0.99999…. in the form p/q . Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.

Solution:

Assume that x = 0.9999…..Eq (a)

Multiplying both sides by 10,

10x = 9.9999…. Eq. (b)

Eq.(b) – Eq.(a), we get

(10x = 9.9999)-(x = 0.9999…)

9x = 9

x = 1

The difference between 1 and 0.999999 is 0.000001 which is negligible.

Hence, we can conclude that, 0.999 is too much near 1, therefore, 1 as the answer can be justified.

5. What can the maximum number of digits be in the repeating block of digits in the decimal expansion of 1/17 ? Perform the division to check your answer.

Solution:

1/17

Divide :

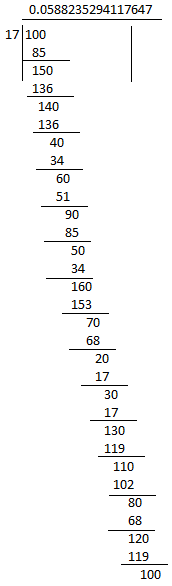
6. Look at several examples of rational numbers in the form p/q (q ≠ 0), where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?

Solution:

We observe that when q is 2, 4, 5, 8, 10… Then the decimal expansion is terminating. For example:

1/2 = 0. 5, denominator q = 2¹

7/8 = 0. 875, denominator q =2³

4/5 = 0. 8, denominator q = 5¹

We can observe that the terminating decimal may be obtained in the situation where prime factorization of the denominator of the given fractions has the power of only 2 or only 5 or both.

7. Write three numbers whose decimal expansions are non-terminating non-recurring.

Solution:

We know that all irrational numbers are non-terminating non-recurring. three numbers with decimal expansions that are non-terminating non-recurring are:

1. √3 = 1.732050807568
2. √26 =5.099019513592
3. √101 = 10.04987562112

8. Find three different irrational numbers between the rational numbers 5/7 and 9/11.

Solution:

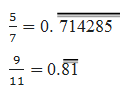
Three different irrational numbers are:

1. 0.73073007300073000073…
2. 0.75075007300075000075…
3. 0.76076007600076000076…

9.  Classify the following numbers as rational or irrational according to their type:

(i)√23

Solution:

√23 = 4.79583152331…

Since the number is non-terminating non-recurring therefore, it is an irrational number.

(ii)√225

Solution:

√225 = 15 = 15/1

Since the number can be represented in p/q form, it is a rational number.

(iii) 0.3796

Solution:

Since the number,0.3796, is terminating, it is a rational number.

(iv) 7.478478

Solution:

The number,7.478478, is non-terminating but recurring, it is a rational number.

(v) 1.101001000100001…

Solution:

Since the number,1.101001000100001…, is non-terminating non-repeating (non-recurring), it is an irrational number.

Exercise 1.4

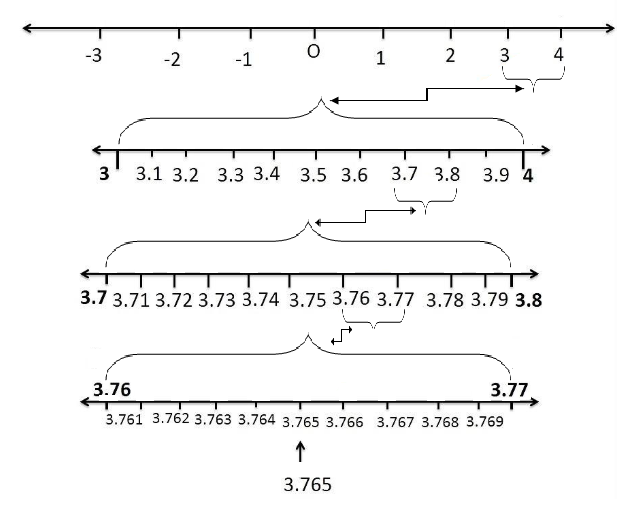
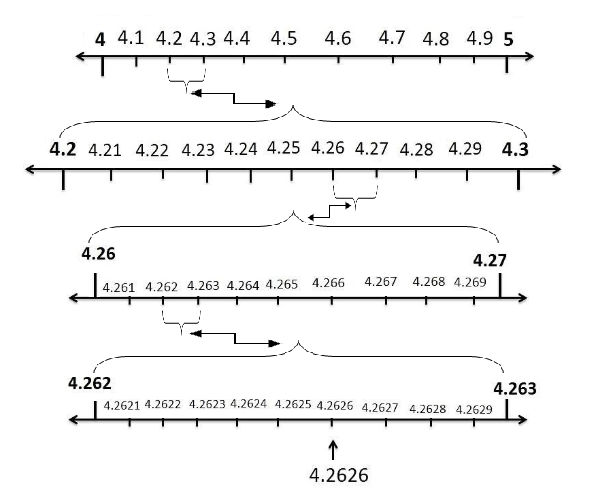
1. Visualise 3.765 on the number line, using successive magnification.

Solution:

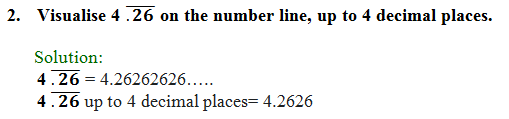
Exercise 1.5

1. Classify the following numbers as rational or irrational:

(i) 2 –√5

Solution:

We know that, √5 = 2.2360679…

Here, 2.2360679…is non-terminating and non-recurring.

Now, substituting the value of √5 in 2 –√5, we get,

2-√5 = 2-2.2360679… = -0.2360679

Since the number, – 0.2360679…, is non-terminating non-recurring, 2 –√5 is an irrational number.

(ii) (3 +√23)- √23

Solution:

(3 +√23) –√23 = 3+√23–√23

= 3

= 3/1

Since the number 3/1 is in p/q form, (3 +√23)- √23 is rational.

(iii) 2√7/7√7

Solution:

2√7/7√7 = ( 2/7)× (√7/√7)

We know that (√7/√7) = 1

Hence, ( 2/7)× (√7/√7) = (2/7)×1 = 2/7

Since the number, 2/7 is in p/q form, 2√7/7√7 is rational.

(iv) 1/√2

Solution:

Multiplying and dividing numerator and denominator by √2 we get,

(1/√2) ×(√2/√2)= √2/2 ( since √2×√2 = 2)

We know that, √2 = 1.4142…

Then, √2/2 = 1.4142/2 = 0.7071..

Since the number , 0.7071..is non-terminating non-recurring, 1/√2 is an irrational number.

(v) 2

Solution:

We know that, the value of = 3.1415

Hence, 2 = 2×3.1415.. = 6.2830…

Since the number, 6.2830…, is non-terminating non-recurring, 2 is an irrational number.

2. Simplify each of the following expressions:

(i) (3+√3)(2+√2)

Solution:

(3+√3)(2+√2 )

Opening the brackets, we get, (3×2)+(3×√2)+(√3×2)+(√3×√2)

= 6+3√2+2√3+√6

(ii) (3+√3)(3-√3 )

Solution:

(3+√3)(3-√3 ) = 3²-(√3)² = 9-3

= 6

(iii) (√5+√2)²

Solution:

(√5+√2)² = √5²+(2×√5×√2)+ √2²

= 5+2×√10+2 = 7+2√10

(iv) (√5-√2)(√5+√2)

Solution:

(√5-√2)(√5+√2) = (√5²-√2²) = 5-2 = 3

3. Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter, (say d). That is, π =c/d. This seems to contradict the fact that π is irrational. How will you resolve this contradiction?

Solution:

There is no contradiction. When we measure a value with a scale, we only obtain an approximate value. We never obtain an exact value. Therefore, we may not realize whether c or d is irrational. The value of π is almost equal to 22/7 or 3.142857…

4. Represent (√9.3) on the number line.

Solution:

Step 1: Draw a 9.3 units long line segment, AB. Extend AB to C such that BC=1 unit.

Step 2: Now, AC = 10.3 units. Let the center of AC be O.

Step 3: Draw a semi-circle of radius OC with center O.

Step 4: Draw a BD perpendicular to AC at point B intersecting the semicircle at D. Join OD.

Step 5: OBD, obtained, is a right angled triangle.

Here, OD 10.3/2 (radius of semi-circle), OC = 10.3/2 , BC = 1

OB = OC – BC

⟹ (10.3/2)-1 = 8.3/2

Using Pythagoras theorem,

We get,

OD²=BD²+OB²

⟹ (10.3/2)² = BD²+(8.3/2)²

⟹ BD^{2 =} (10.3/2)²-(8.3/2)²

⟹ (BD)² = (10.3/2)-(8.3/2)(10.3/2)+(8.3/2)

⟹ BD² = 9.3

⟹ BD =  √9.3

Thus, the length of BD is √9.3.

Step 6: Taking BD as radius and B as center draw an arc which touches the line segment. The point where it touches the line segment is at a distance of √9.3 from O as shown in the figure.

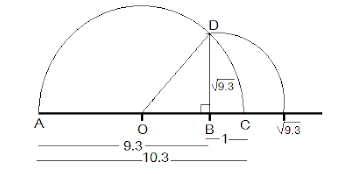
5. Rationalize the denominators of the following:

(i) 1/√7

Solution:

Multiply and divide 1/√7 by √7

(1×√7)/(√7×√7) = √7/7

(ii) 1/(√7-√6)

Solution:

Multiply and divide 1/(√7-√6) by (√7+√6)

[1/(√7-√6)]×(√7+√6)/(√7+√6) = (√7+√6)/(√7-√6)(√7+√6)

 

= (√7+√6)/√7²-√6² [denominator is obtained by the property, (a+b)(a-b) = a²-b²]

= (√7+√6)/(7-6)

= (√7+√6)/1

= √7+√6

(iii) 1/(√5+√2)

Solution:

Multiply and divide 1/(√5+√2) by (√5-√2)

[1/(√5+√2)]×(√5-√2)/(√5-√2) = (√5-√2)/(√5+√2)(√5-√2)

 

= (√5-√2)/(√5²-√2²) [denominator is obtained by the property, (a+b)(a-b) = a²-b²]

= (√5-√2)/(5-2)

= (√5-√2)/3

(iv) 1/(√7-2)

Solution:

Multiply and divide 1/(√7-2) by (√7+2)

1/(√7-2)×(√7+2)/(√7+2) = (√7+2)/(√7-2)(√7+2)

= (√7+2)/(√7²-2²) [denominator is obtained by the property, (a+b)(a-b) = a²-b²]

= (√7+2)/(7-4)

= (√7+2)/3

Exercise 1.6

1. Find:

(i)64^1/2

Solution:

64^1/2 = (8×8)^1/2

= (8²)^½

= 8¹ [⸪2×1/2 = 2/2 =1]

= 8

(ii)32^1/5

Solution:

32^1/5 = (2⁵)^1/5

= (2⁵)^⅕

= 2¹ [⸪5×1/5 = 1]

= 2

(iii)125^1/3

Solution:

(125)^1/3 = (5×5×5)^1/3

= (5³)^⅓

= 5¹ (3×1/3 = 3/3 = 1)

= 5

2. Find:

(i) 9^3/2

Solution:

9^3/2 = (3×3)^3/2

= (3²)^3/2

= 3³ [⸪2×3/2 = 3]

=27

(ii) 32^2/5

Solution:

32^2/5 = (2×2×2×2×2)^2/5

= (2⁵)^2⁄5

= 2² [⸪5×2/5= 2]

= 4

(iii)16^3/4

Solution:

16^3/4 = (2×2×2×2)^3/4

= (2⁴)^3⁄4

= 2³ [⸪4×3/4 = 3]

= 8

(iv) 125^-1/3

125^-1/3 = (5×5×5)^-1/3

= (5³)^-1⁄3

= 5^-1 [⸪3×-1/3 = -1]

= 1/5

3. Simplify:

(i) 2^2/3×2^1/5

Solution:

2^2/3×2^1/5 = 2^(2/3)+(1/5) [⸪Since, a^m×aⁿ=a^m+n____ Laws of exponents]

= 2^13/15 [⸪2/3 + 1/5 = (2×5+3×1)/(3×5) = 13/15]

(ii) (1/3³)⁷

Solution:

(1/3³)⁷ = (3^-3)⁷ [⸪Since,(a^m)ⁿ = a^{m x n}____ Laws of exponents]

= 3^-21

(iii) 11^1/2/11^1/4

Solution:

11^1/2/11^1/4 = 11^(1/2)-(1/4)

= 11^1/4 [⸪(1/2) – (1/4) = (1×4-2×1)/(2×4) = 4-2)/8 = 2/8 = ¼ ]

(iv) 7^1/2×8^1/2

Solution:

7^1/2×8^1/2 = (7×8)^1/2 [⸪Since, (a^m×b^m = (a×b)^m ____ Laws of exponents]

= 56^1/2