NCERT Solutions Maths Ch-1 Sets for Class 11th
Chapter 1 of the NCERT Class 11 Mathematics textbook is titled “Sets”. In this chapter, the concept of a set, its representation, and types are introduced. A set is defined as a well-defined collection of distinct objects or elements. These elements can be anything: numbers, letters, or even abstract concepts. Sets are represented in two primary ways: Roster or Tabular Form and Set-builder Form. The chapter explores various operations on sets such as union, intersection, and complement, as well as Venn diagrams for visualizing relationships between sets. Key concepts like subset, proper subset, and universal set are also covered, along with the notion of cardinality (the number of elements in a set). Understanding sets is fundamental to various branches of mathematics, as it lays the groundwork for further study in areas like probability, algebra, and geometry. The chapter helps in building a strong foundation for higher-level mathematical concepts.
NCERT Solutions of Class 11th Chapter 1 Sets Exercises
Q1. Which of the following are sets? Justify your answer.
(i)The collection of all the months of a year beginning with the letter J.
(ii)The collection of ten most talented writers of India.
(iii)A team of eleven best-cricket batsmen of the world.
(iv)The collection of all boys in your class.
(v)The collection of all natural numbers less than 100.
(vi)A collection of novels written by the writer Munshi Prem Chand.
(vii)The collection of all even integers.
(viii)The collection of questions in this Chapter.
(ix)A collection of most dangerous animals of the world.
A.1. (i)The collection of all months of a year with J as initial are January, June and July. Hence, it is a well-defined and is therefore a set January,June,July .
(ii)The collection of ten most talented writers of India is not well-defined as it may vary from one person to another. Hence, it is not a set.
(iii)The team of 11 best-cricket batsmen of the world is not well-defined as it may vary from one parson to another as they may vary from one person to another. Hence, it is not a set.
(iv)The collection of all boys in your class is well-defined as your-class is fixed. Hence, it is a set.
(v)The collection of all natural numbersless than 100 will be from 1 to 99. Hence, it is well-defined and is therefore a set.
(vi)Novels written by writer Munshi Prem cham is a well-defined collection as he is no more so. Hence it is a set.
(vii)The collection of all even integers is well-defined and hence is a set.
(viii)The collection of questions in this chapter is well-defined and hence is a set.
(ix)The collection of most dangerous animals of the world is not well-defined as it may vary from one person to another.
Q2. Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or ∉ in the blank spaces:
(i)5. . .A(ii)8 . . . A (iii)0. . .A
(iv) 4. . . A (v) 2. . .A (vi) 10. . .A
A.2. (i)5 ∈ A(ii)8 ∉ A(iii)0 ∉ A
(iv)4 ∈ A(v)2 ∈ A(vi)10 ∉ A
Q3. Write the following sets in roster form:
(i)A = {x : x is an integer and –3< x < 7}
(ii) B = {x : x is a natural number less than 6}
(iii) C = {x : x is a two-digit natural number such that the sum of its digits is 8}
(iv) D = {x : x is a prime number which is divisor of 60}
(v) E = The set of all letters in the word TRIGONOMETRY
(vi) F = The set of all letters in the word BETTER
A.3. (i)A = {– 3, –2, –1, 0, 1, 2, 3, 4, 5, 6}
(ii)B = {1, 2, 3, 4, 5}
(iii)C = {17, 26, 35, 44, 53, 62, 71, 80}
(iv)x = Prime number which are divisor of 60
Factors of 60 are 1,2,3,4,5,6,10,12,15,20,30,60
Hence, x = 2, 3, 5
⸫D = {2, 3, 5}
(v) E = {T, R, I, G, O, N, M, E, Y}
(vi) F = {B, E, T, R}
Q4. Write the following sets in the set-builder form:
(i)(3, 6, 9, 12} (ii) {2,4,8,16,32} (iii) {5, 25, 125, 625}
(iv) {2, 4, 6, . . .} (v) {1,4,9, . . .,100}
A.4. (i) {3,6,9,12}={3 × 1, 3 × 2, 3 × 3, 3 × 4}
= {x : x = 3n, n is natural number and 1≤ n ≤ 4}
(ii){2,4,8,16,32}={21, 22, 23, 24, 25}
={x : x = 2n, n is natural number and 1 ≤ n ≤ 5}
(iii){5,25,125,625}={51, 52, 53, 54}
={x : x = 5n, n is natural number and 1 ≤ n ≤ 4}
(iv){2,4,6,}={2 × 1, 2 × 2, 2 × 3, …}
={x : x = 2n, n is a natural number}
(v){1,4,9, …, 100}={12, 22, 32, …, 102}
= {x : x = n2, x is a natural number and 1 ≤ n ≤ 10}
Q5. List all the elements of the following sets :
(i)A = {x : x is an odd natural number}
(ii) B = {x : x is an integer, −12<x<92
(iii) C = {x : x is an integer, x2≤4 }
(iv)D = {x : x is a letter in the word “LOYAL”}
(v) E = {x : x is a month of a year not having 31 days}
(vi)F = {x : x is a consonant in the English alphabet which precedes k }.
A.5. (i)A = {1, 3, 5, 7, …}
(ii)B ={0,1,2,3,4} (as 92 =4.5 and −12 = –0.5)
(iii)x2 ≤ 4
x2 ≤ 22
x ≤ ± 2
So, C ={–2, –1,0,1,2}
(vi)D = {L, O, Y, A}
(v)E = {February, April, June, September, November}
(vi)F = {b, c, d, f, g, h, j}
Q6. Match each of the set on the left in the roster form with the same set on the right described in set-builder form:
(i){1, 2, 3, 6} (a) {x : x is a prime number and a divisor of 6}
(ii) {2, 3} (b) {x : x is an odd natural number less than 10}
(iii) {M,A,T,H,E,I,C,S} (c){x : x is natural number and divisor of 6}
(iv) {1, 3, 5, 7, 9} (d){x : x is a letter of the word MATHEMATICS}.
A.6. (i)(i) (c)
(ii) (a)
(iii) (d)
(iv) (b)
Q.1: Which of the following given below is null set?
(i). Set of odd natural numbers which is divisible by 2.
(ii). Set of even numbers which are prime
(iii). {x: x is a natural number, x<5 and x>7}
(iv). {y: y is a point common to any two parallel lines}
Solution:
(i)There is no odd number that can be divided by 2.
⸫The given set is a null set.
(ii)An even prime number is 2. Hence, the set will have 2 as element. ⸫ The given set is not a null set.
(iii)As there is no natural number which is both less than 5 and greater than 7. ⸫ The given set is a null set.
(iv)Two parallel lines never meets and hence no common point. ⸫ The given set is a null set.
Q.2: State whether the following sets are infinite or finite:
(i). A set of months of a year.
(ii). {1, 2, 3 ….}
(iii). {1, 2, 3…99, 100}
(iv). The set of positive integers which are greater than 100.
(v). The set of prime numbers which are less than 99
Solution:
(i)The set of months of a year has 12 elements. Here, the set is finite.
(ii)The given set has the natural number as its elements. Hence, the set is infinite.
(iii)The given set has 100 elements i.e., from 1 to 100. Hence, the set is finite.
(iv)There are infinite numbers of positive integers greater than 100. Hence the set is infinite.
(v)The numbers of prime number less than 99 is finite. Hence, the set is finite.
Q.3: State whether the following sets are infinite or finite:
(i). The set of lines parallel to the x – axis.
(ii). The set of letters in the vowels.
(iii). The set of numbers multiple of 10.
(iv). The set of humans living on Earth.
(v). The set of circles passing through the origin (0, 0).
Solution:
(i)We can draw infinite number of lines parallel to x-axis.
⸫The set is infinite.
(ii)There are 26 letters in the English alphabet.
⸫The set is finite.
(iii)There are infinite number which are a multiple of 5.
⸫The set is infinite
(iv)The numbers of animals living on earth are finite.
⸫The set is finite.
(v)There can be infinite number of circular passing through origin (0,0).
⸫The set is infinite.
Q.4: In the following set given below, state whether A = B or not:
(i). A = {w, x, y, z}
B = {z, y, x, w}
(ii). A = {5, 9, 13, 17}
B = {9, 5, 17, 19}
(iii). A = {4, 2, 6, 10, 8}
B = {x: x is positive even integer and x≤10 }
(iv). A = {x: x is a multiple of 10}
B = {10, 15, 20, 25, 30 …}
Solution:
(i)As A and B has a, b, c and d as elements and are exactly the same, Hence, A = B.
(ii)Hence, 12 ∈ A but 12 ∉ B
Similarly 18 ∈ B but 18 ∉ A.
So, A ≠ B.
(iii)A = {2,4,6,8,10} and B = {2,4,6,8,10}
So, A=B.
(v)A={10,20,30,40, …} and B={10,15,20,25,30, …}
So, A ≠ B.
Q.5 In the following set given below, is the pair of sets equal?
(i). A = {3, 4}
B = {y: y is solution of y²+5y+6=0}
(ii). A = {a: a is a letter in the word FOLLOW}
B = {b: b is a letter in the word WOLF}
Solution:
(i)A = {2, 3)
B = {x : x is solution of x2 + 5x + 6 = 0}
So, x2 + 5x + 6 = 0
x2 + 2x + 3x + 6 = 0
x(x+2) + 3(x+2) = 0
(x+2)(x+3) = 0
x = –2, –3
So, B = {–2, –3}
So, A ≠ B.
(ii)A = {x : x is a letter in word FOLLOW}
A = {F, O, L, W}
B = {x : x is a letter in word WOLF}
B = {W, O, L, F}
So, A = B as the elements are all same.
Q.6: From the following sets, select equal sets:
A = {2, 4, 8, 12}
B = {1, 2, 3, 4}
C = {4, 8, 12, 14}
D = {3, 1, 4, 2}
E = {–1, 1}
F = {0, a}
G = {1, –1}
H = {0, 1}
Solution:
B = D = {1, 2, 3, 4} = {3, 1, 4, 2}
E = G = {–1, 1} = {1, –1}.
Q1. Make correct statements by filling in the symbols ⊂or ₡ in the blank spaces :
(i) { 2, 3, 4 } . . . { 1, 2, 3, 4,5 } (ii) { a, b, c } . . . { b, c, d }
(iii) {x : x is a student of Class XI of your school}. . .{x : x student of your school}
(iv) {x : x is a circle in the plane} . . .{x : x is a circle in the same plane with radius 1 unit}
(v) {x : x is a triangle in a plane} . . . {x : x is a rectangle in the plane}
(vi) {x : x is an equilateral triangle in a plane} . . . {x : x is a triangle in the same plane}
(vii) {x : x is an even natural number} . . . {x : x is an integer}
Solution:
(i){2,3,4} ⊂ {1,2,3,4,5}
(ii){a, b, c} ₡ {b, c, d}
(iii){x : x is a student of class XI of yours school} ⊂ {x : x is a student of your school}
(iv)As any circle in the plane can have radius more or less than 1 unit.
(x : x is a circle in the plane) ₡ {x : x is a circle in the same plane with radius 1 unit}
(v)As a triangle can never be a rectangle.
{x : x is a triangle in a plane} ₡ {x : x is a triangle in the same plane}
(vi)Any triangle in a plane can be scaler, isosceles, equilateral.
So. {x : x is a equilateral triangle in a plane} ⊂ {x : x is a triangle in the same plane}
(vii)As all even natural number is also an integer.
{x : x is an even natural number} ⊂ {x : x is an integer}.
Q2. Examine whether the following statements are true or false:
(i) { a, b } ₡ { b, c, a }
(ii) { a, e } ⊂ { x : x is a vowel in the English alphabet}
(iii) { 1, 2, 3 } ⊂ { 1, 3, 5 }
(iv) { a } ⊂ { a, b, c }
(v) { a } ∈ { a, b, c }
(vi) { x : x is an even natural number less than 6} ⊂ { x : x is a natural number which divides 36}
Solution
(i)False as every element of set {a, b} is also an element of {b, c, a} hence {a, b } ⊂ { b, c, a }.
(ii)True as every element in {a, e} is also a vowel in English alphabet.
(iii)False as 2 ∈ {1, 2, 3} but 2 ∉ {1, 3, 5}.
(iv)True as a ∈ {a} is also a ∈ {a, b, c}
(v)False as a ∈ {a, b, c} but {a} ∈ {a, b, c}
(vi){x : x is an even natural number less than 6} = {2, 4}
{x : x is a natural number which divides 36} = {1, 2, 3, 4, 6, 9, 12, 18, 36}
As {2, 4} ⊂ {1, 2, 3, 4, 6, 9, 12, 18, 36}
It is true.
Q.3. Let A = { 1, 2, { 3, 4 }, 5 }. Which of the following statements are incorrect and why?
(i) {3, 4} ⊂ A (ii) {3, 4} ∈ A (iii) {{3, 4}} ⊂ A
(iv) 1 ∈ A (v) 1 ⊂ A (vi) {1, 2, 5} ⊂ A
(vii) {1, 2, 5} ∈ A (viii) {1, 2, 3} ⊂ A (ix) ϕ∈ A
(x) ϕ⊂ A (xi) { ϕ } ⊂ A
Solution:
(i)False as 3 ∉ A and 4 ∉ 4. So, {3, 4} ⊂ A.
(ii)True as {3, 4} ∈ A. i.e, {3, 4} is an element of A.
(iii)True as {3, 4} ∈ A so, {3, 4} ⊂ A.
(iv)True as 1 is an element of A.
(v)False as 1 is not a set so it cannot be a subset of A.
(vi)True as 1 ∈ A, 2 ∈ A and 5 ∈ A. so, {1, 2, 5} ⊂ A.
(vii)False as {1, 2, 5} is not an element of A.
(viii)False of 3 ∉ A.
(ix)False as ϕ is not an element of A.
(x)True, ϕ ⸦ A as ϕ is a subset of every set.
(xi)False, as ϕ is not an element of A.
Q4. Write down all the subsets of the following sets
(i) {a} (ii) {a, b}
(iii) {1, 2, 3} (iv) ϕ
Solution:
(i)Subset of {a} = {a}, ϕ .
(ii)Subset of {a, b} = ϕ ,{a},{b},{a, b}
(iii)Subset of {1,2,3} = ϕ ,{1},{2},{3}, {1,2}, {1,3}, {2,3}, {1,2,3}.
(iv)Subset of ϕ = ϕ .
Q5. How many elements has P(A), if A = ϕ ?
Solution
As A= ϕ , no elements
n(A) = 0 = m
So, n[P(A)] = 2m = 20 = 1.
Q6. Write the following as intervals:
(i) {x : x ∈ R, – 4 <x < 6} (ii) {x : x ∈ R, – 12 < x < –10}
(iii) {x : x ∈ R, 0 ≤ x < 7} (iv) {x : x ∈ R, 3 ≤ x ≤ 4}
Solution
(i)As x does not include –4 while 6 is included.
(–4, 6].
(ii)As x does not include both –12 and –10.
(–12, –10)
(iii)As x includes 0 but does not includes 7.
[0, 7)
(iv)As includes both 3 and 4
[3, 4]
Q7. Write the following intervals in set-builder form :
(i) (– 3, 0) (ii) [6 , 12] (iii) (6, 12] (iv) [–23, 5)
Solution
(i)[–3, 0] = {x : x such that x ∈ R, –3 < x <0}
(ii)[6, 12] = {x : x ∈ R, 6 ≤ x ≤ 12}
(iii)(6, 12] = {x : x ∈ R, 6 < x ≤ 12}
(iv)[–23, 5) = {x : x ∈ R, –23 ≤ x < 5}
Q8. What universal set(s) would you propose for each of the following:
(i)The set of right triangles. (ii) The set of isosceles triangles.
Solution
(i)The set of all triangles. U= {x : x is a triangle in a plane}
(ii) The set of all triangles. U= {x : x is a triangle in a plane}
Q9. Given the sets A = {1, 3, 5}, B = {2, 4, 6} and C = {0, 2, 4, 6, 8}, which of the following may be considered as universal set (s) for all the three sets A, B and C
(i) {0, 1, 2, 3, 4, 5, 6}
(ii) ϕ
(iii) {0,1,2,3,4,5,6,7,8,9,10}
(iv) {1,2,3,4,5,6,7,8}
Solution
Universal set of A, B and C must includes all elements of A, B and C, i.e. 0,1,2,3,4,5,6,8.
So, the universal set of A, B and C is (iii) {0,1,2,3,4,5,6,7,8,9,10}.
Q1. Find the union of each of the following pairs of sets:
(i) X = {1, 3, 5} Y = {1, 2, 3}
(ii) A = [ a, e, i, o, u} B = {a, b, c}
(iii) A = {x : x is a natural number and multiple of 3}
B = {x : x is a natural number less than 6}
(iv) A = {x : x is a natural number and 1 < x ≤ 6 }
B = {x : x is a natural number and 6 < x <10 }
(v) A = {1, 2, 3}, B = ϕ
ans.1. (i)X∪ Y = {1,3,5}∪ {1,2,3} = {1,2,3,5}.
(ii)A ∪B = {a, e, i, o, u} ∪{a, b, c} = {a, b, c, e, i, o, u}
(iii)A = {3, 6, 9, 12 …}
B = {1, 2, 3, 4, 5}
So, A∪ B = {3, 6, 9, 12, …}∪ {1, 2, 3, 4, 5}
= {1, 2, 3, 4, 5, 6, 9, 12 …}
(iv)A = {2, 3, 4, 5, 6}
B = {7, 8, 9}
So, A∪ B = {2, 3, 4, 5, 6}∪ {7, 8, 9} = {2, 3, 4, 5, 6, 7, 8, 9}
(v)A ∪B = {1, 2, 3} ∪ ϕ = {1, 2, 3}.
Q2. Let A = { a, b }, B = { a, b, c}. Is A ⊂ B ? What is A ∪ B ?
ans.2. Given,A = {a, b}
B = {a, b, c}
Yes A ⊂ B as a, b ∈ A and a, b ∈ B.
And A ∪ B = {a, b} ∪{a, b, c} = {a, b, c} = B
Q3.If A and B are two sets such that A ⊂ B, then what is A ∪ B ?
ans.3.If A ⸦ B then let a ∈ A and also a ∈ B.
but b ∈ B and b ∉ A i.e, A = {a} and B = {a, b}
So, A ∪ B = {x : x ∈ A or x ∈ B}
= {a, b}
= B
Q4. If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8 } and D = { 7, 8, 9, 10 }; find
(i) A ∪B (ii) A ∪ C (iii) B ∪C (iv) B ∪ D
(v) A ∪B ∪C (vi) A ∪ B ∪ D (vii) B ∪ C ∪ D
ans.4. (i)A ∪ B = {1, 2, 3, 4} ∪ {3, 4, 5, 6}
= {1, 2, 3, 4, 5, 6}
(ii)A ∪C = {1, 2, 3, 4} ∪ {5, 6, 7, 8}
= {1, 2, 3, 4, 5, 6, 7, 8}
(iii)B ∪ C = {3, 4, 5, 6} ∪{5, 6, 7, 8}
= {3, 4, 5, 6, 7, 8}
(iv)B ∪D = {3, 4, 5, 6} ∪{7, 8, 9, 10}
= {3, 4, 5, 6, 7, 8, 9, 10}
(v)A ∪ B ∪C = (A ∪B) ∪ C = {1,2,3,4,5,6} ∪{5,6,7,8}
= {1, 2, 3, 4, 5, 6, 7, 8}
(vi)A ∪B ∪ D = (A ∪ B) ∪ D = {1,2,3,4,5,6} ∪ {7,8,9,10}
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(vii)B ∪ C ∪ D = (B ∪ C) ∪ D = {3,4,5,6,7,8} ∪ {7,8,9,10}
= {3, 4, 5, 6, 7, 8, 9, 10}
Q5. Find the intersection of each pair of sets of question 1 above.
ans.5. (i)X ∩ Y = {1,3,5} ∩ {1,2,3} = {1,3}
(ii)A = {a, e, i, o, u} ∩ {a, b, c} = {a}
(iii)A ∩ B = {3,6,9,12 …} ∩ {1,2,3,4,5}
= {3}
(iv)A ∩ B = {2,3,4,5,6} ∩ {7,8,9} = ϕ
(v)A ∩ B = {1,2,3} ∩ ϕ = ϕ
Q6. If A = { 3, 5, 7, 9, 11 }, B = {7, 9, 11, 13}, C = {11, 13, 15}and D = {15, 17}; find
(i) A ∩ B(ii)B ∩ C (iii) A ∩ C ∩ D
(iv) A ∩ C (v) B ∩ D (vi) A ∩ (B ∪ C)
(vii) A ∩ D (viii) A ∩ (B ∪ D) (ix)(A ∩ B) ∩ (B ∪ C )
(x) (A ∪ D) ∩ (B ∪ C)
ans.6. (i)A ∩ B = {3,5,7,9,11} ∩ {7,9,11,13}
= {7, 9, 11}
(ii)B ∩ C = {7,9,11,13} ∩ {11,13,15}
= {11,13}
(iii)A ∩ C ∩ D = (A ∩ C) ∩ D
= [{3,5,7,9,11} ∩ {11,13,15}] ∩ {15,17}.
= {11} ∩ {15,17} = ϕ .
(iv)A ∩ C = {3,5,7,9,11} ∩ {11,13,15}.
= {11}
(v)B ∩ D = {7,9,11,13} ∩ {15,17}= ϕ
(vi)A ∩ (B∪ C) = {3,5,7,9,11} ∩ [{7,9,11,13}∪ {11,13,15}]
= {3,5,7,9,11} ∩ {7,9,11,13,15}.
= {7,9,11}
(vii)A ∩ D = {3,5,7,9,11} ∩ {15,17} = ϕ .
(viii)A ∩ (B ∪ D) = {3,5,7,9,11} ∩ [{7,9,11,13} ∪ {15,17}]
= {3,5,7,9,11} ∩ {7,9,11,13,15,17}
= {7,9,11}
(ix)(A ∩ B) ∩ (B ∪ C) = [{3,5,7,9,11} ∩{7,9,11,13}] ∩ [{7,9,11, 13} ∪ {11,13, 15}]
= {7,9,11} ∩ {7,9,11,13,15}
= {7,9,11}.
(x)(A ∪ D) ∩ (B ∪ C) = [{3,5,7,9,11} ∪ {15,17}] ∩ [{7, 9, 11, 13} ∪ {11, 13, 15}
={3,5,7,9,11,15,17} ∩ {7,9,11,13,15}
={7,9,11,15}.
Q7. If A = {x : x is a natural number }, B = {x : x is an even natural number}
C = {x : x is an odd natural number} and D = {x : x is a prime number }, find
A ∩ B (ii) A ∩ C (iii) A ∩ D
(iv) B ∩ C (v) B ∩ D (vi) C ∩ D
ans.7. A = {1,2,3,4,5, 6, …}
B = {2,4,6, …}
C = {1,3,5, …}
D = {2,3,5, …,}
(i)A ∩ B = {1,2,3,4 …} ∩ {2,4,6, …} = {2,4,6 …} = B.
(ii)A ∩ C = {1,2,3,4, …} ∩ {1,3,5 …} = {1,3,5, …} = C.
(iii)B ∩ C = {2,4,6, …} ∩ {1,3,5, …} = ϕ .
(iv)B ∩ D = {2,4,6 …} ∩ {2,3,5 …} = {2}
(v)C ∩ D = {1,3,5, …} ∩ {2,3,5 …} = {3,5,7 …} = {x : x is odd prime number}
Q.8. Which of the following pairs of sets are disjoint
(i){1, 2, 3, 4} and {x : x is a natural number and 4≤x≤6 }
(ii) {a, e, i, o, u } and { c, d, e, f }
(iii) {x : x is an even integer} and {x : x is an odd integer}
ans.8. (i){1,2,3,4} ∩ {x : x is a natural number and 4 ≤ x ≤ 6}
{1, 2, 3, 4} ∩ {4, 5, 6}
{4} ≠∅
Hence, the given pair of set is not disjoint.
(ii){a, e, i, o, u} ∩ {c, d, e, f}
{e} ≠∅
Hence, the given pair of set is not disjoint.
(iii){x: x is an even integer} ∩ {x: x is are odd integer}.
=∅
As there is no integer which is both even and odd at the same time.
⸫ Given pair of set are disjoint.
Q9. If A = {3, 6, 9, 12, 15, 18, 21}, B = { 4, 8, 12, 16, 20},
C = {2, 4, 6, 8, 10, 12, 14, 16}, D = {5, 10, 15, 20}; find
(i) A – B (ii) A – C (iii) A – D (iv) B – A
(v) C – A (vi) D – A (vii) B – C (viii) B – D
(ix) C – B (x) D – B (xi) C – D (xii) D – C
ans.9. (i)A – B = {3,6,9,12,15,18,21} – {4,8,12,16,20}
= {3,6,9,15,18,21}
(ii)A – C = {3,6,9,12,15,18,21} – {2,4,6,8,10,12,14,16}
= {3,9,15,18,21}
(iii)A – D = {3,6,9,12,15,18,21} – {5,10,15,20}
= {3,6,9,12,18,21}
(iv)B – A = {4,8,12,16,20} – {3,6,9,12,15,18,21}
= {4,8,16,20}
(v)C – A = {2,4,6,8,10,12,14,16} – {3,6,9,12,15,18,21}
= {2,4,8,10,14,16}
(vi)D – A = {5,10,15,20} – {3,6,9,12,15,18,21}
={5,10,20}
(vii)B – C={4,8,12,16,20} – {2,4,6,8,10,12,14,16}
={20}
(viii)B – D ={4,8,12,16,20} – {5,10,15,20}
= {4,8,12,16}
(ix)C – B = {2,4,6,8,10,12,14,16} – {4,8,12,16,20}
= {2,6,10,14}
(x)D – B = {5,10,15,20} – {4,8,12,16,20}
= {5,10,15}
(xi)C – D = {2,4,6,8,10,12,14,16} – {5,10,15,20}
= {2,4,6,8,12,14,16}
(xii)D – C = {5,10,15,20} – {2,4,6,8,10,12,14,16}
= {5,15,20}
Q10. If X= { a, b, c, d } and Y = { f, b, d, g}, find
(i)X – Y (ii)Y – X (iii) X ∩Y
ans.10. (i)X – Y = {a, b, c, d} – (f, b, d, g}
= {a, c}
(ii) Y – X = {f, b, d, g} – {a, b, c, d}
= {f, g}
(iii)X ∩ Y = {a, b, c, d} ∩ {f, b, d, g}
= {b, d}.
Q11. If R is the set of real numbers and Q is the set of rational numbers, then what is R – Q?
ans.11. R – Q = {x: x is a real number but not rational number}
= {x: x is an irrational number}
Since real number = rational number + irrational number
Q12. State whether each of the following statement is true or false. Justify your answer.
(i) {2, 3, 4, 5} and {3, 6} are disjoint sets.
(ii) {a, e, i, o, u} and {a, b, c, d}are disjoint sets.
(iii) {2, 6, 10, 14} and {3, 7, 11, 15} are disjoint sets.
(iv) {2, 6, 10} and {3, 7, 11} are disjoint sets.
Ans.12. (i)False, as {2,3,4,5} ∩ {3,6} = {3} ≠ ϕ .Hence sets are not disjoint.
(ii)False as {a, e, i, o, u} ∩ {a, b, c, d} = {a} ≠ ϕ Hence sets are not disjoint.
(iii)True as {2,6,10,14} ∩ {3,7,11,15} = ϕ . Hence sets are disjoint.
(iv)True as {2,6,10} ∩ {3,7,11}= ϕ . Hence sets are disjoint.
Q1. Let U = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }, A = { 1, 2, 3, 4}, B = { 2, 4, 6, 8 } andC = { 3, 4, 5, 6 }.
Find (i) A ‘ (ii)B ‘ (iii)(A ∪ C) ‘ (iv)(A ∪ B) ‘
(v) (A ‘ ) ‘ (vi) (B – C) ‘
A.1. (i)A ‘ = U – A = {1,2,3,4,5,6,7,8,9} – {1,2,3,4}
= {5,6,7,8,9}
(ii)B ‘ = U – B = {1,2,3,4,5,6,7,8,9} – {2,4,6,8}
= {1,3,5,7,9}.
(iii)(A ∪C) ‘ = A ‘ ∩ C ‘
= {5,6,7,8,9} ∩ [U – C] [⸪ (i)]
= {5,6,7,8,9} ∩ [{1,2,3,4,5,6,1,8,9} – {3,4,5,6}]
= {5,6,7,8,9} ∩ {1,2,7,8,9}
= {7,8,9}
(iv)(A ∪ B) ‘ = A ‘ ∩ B ‘ [By demorgan’s law]
= {5,6,7,8,9} ∩ {1,3,5,7,9} [⸪ (i) and (ii)]
= {5,7,9}.
(v)(A ‘) ‘ = U – A ‘ = {1,2,3,4,5,6,7,8,9} – {5,6,7,8,9} [⸪ (1)]
= {1,2,3,4} = A
(A ‘) ‘ = A.
(vi)(B – C) ‘ = U – (B – C) = {1,2,3,4,5,6,7,8,9} – [{2, 4, 6, 8} – {3, 4, 5, 6}]
= {1,2,3,4,5,6,7,8,9} – {2,8}
= {1,3,4, 5, 6,7,9}.
Q2. If U = { a, b, c, d, e, f, g, h}, find the complements of the following sets :
(i) A = {a, b, c} (ii) B = {d, e, f, g}
(iii) C = {a, c, e, g} (iv) D = { f, g, h, a}
A.2. (i)A ‘ = U – A = {a, b, c, d, e, f, g, h} – {a, b, c}
= {d, e, f, g, h}
(ii)B ‘ = U – B = {a, b, c, d, e, f, g, h} – {d, e, f, g}
= {a, b, c, h}.
(iii)C ‘ = U – C = {a, b, c, d, e, f, g, h} – {a, c, e, g}.
= {b, d, f, h}
(iv)D ‘ = U – D = {a, b, c, d, e, f, g, h} – {f, g, h, a}
= {b, c, d, e}
Q3. Taking the set of natural numbers as the universal set, write down the complements of the following sets:
(i) {x : x is an even natural number} (ii) { x : x is an odd natural number }
(iii) {x : x is a positive multiple of 3} (iv) { x : x is a prime number }
(v) {x : x is a natural number divisible by 3 and 5}
(vi) {x : x is a perfect square } (vii) { x : x is a perfect cube}
(viii) {x : x + 5 = 8 } (ix) { x : 2x + 5 = 9}
(x) {x : x ≥ 7} (xi) { x : x ∈ N and 2x + 1 > 10 }
A.3. (i){x : x is an odd natural number}
(ii){x : x is an even natural number}
(iii){x : x is not a multiple of 3}
(iv){x : x is a positive composite number and x = 1}
(v){x : x is a natural number not divisible by 3 and 5}.
(vi){x : x is not a perfect square}
(vii){x : x is not a perfect cube}
(viii)We have, x + 5 = 8.
x = 8 – 5 = 3
x = 3
⸫ {x : x ≠ 3, x ϵ N}
(ix)We have,
2x + 5 = 9
2x = 9 – 5
2x = 4
x = 2
⸫{x : x ϵ N and x ≠ 2}
(x){x : x < 7} = {1,2,3,4,5,6}
(xi)We have,
2x + 1 >10
2x >10 – 1
x > 92
⸫ {x:x∈x<92} ={1,2,3,4}
Q4. If U = {1, 2, 3, 4, 5, 6, 7, 8, 9 }, A = {2, 4, 6, 8} and B = { 2, 3, 5, 7}. Verify that
(i) A ∪ B) ‘ = A ‘ ∩ B ‘ (ii) A ∩ B) ‘ = A ‘ ∪B ‘
A.4. (i)L.H.S = (A ∪ B) ‘ = U – (A ∪B)
= {1,2,3,4,5,6,7,8,9} – [{2,4,6,8) ∪ {2,3,5,7}]
= {1,2,3,4,5,6,7,8,9} – {2,3,4,5,6,7,8}
= {1,9}
R.H.S. = A ‘ ∩ B ‘ = [U – A] ∩ [U ∪ B]
= [{1,2,3,4,5,6,7,8,9}–{2,4,6,8}] ∩ [{1,2,3,4,5,6,7,8,9}–{2,3,5,7}]
= {1,3,5,7,9} ∩ {1,4,6,8,9}
= {1,9}
⸫ L.H.S. = R.H.S.
(A B) = A ∩ B.
(ii)L.H.S. = (A ∩ B) ‘ = U – (A ∩ B)
= {1,2,3,4,5,6,7,8,9} – [{2,4,6,8} ∩ {2,3,5,7}]
= {1,2,3,4,5,6,7,8,9} – {2}
= {1,3,4,5,6,7,8,9}
R.H.S. = A ‘ ∪B ‘
= [U – A] ∪[U – B]
= [{1,2,3,4,5,6,7,8,9} – {2,4,6,8}] [{1,2,3,4,5,6,7,8,9} – {2,3,5,7}]
= {1,3,5,7,9} ∪ {1,4,6,8,9}
= {1,3,4,5,6,7,8,9}
⸫ L.H.S. = R.H.S.
(A ∩ B) ‘ = A ‘ ∪ B ‘.
Q5. Draw appropriate Venn diagram for each of the following :
(i) (A ∪ B) ‘ , (ii) A ‘ ∪ B ‘ , (iii) (A ∪ B) ‘ , (iv) A ‘ ∪ B ‘
A.5.
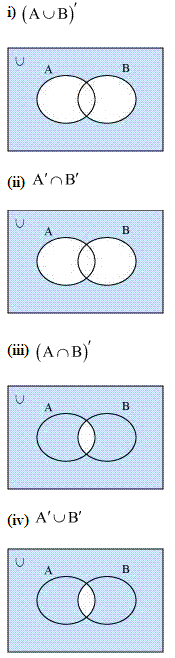
Q.6. Let U be the set of all triangles in a plane. If A is the set of all triangles with at least one angle different from 60°, , what is A ‘?
A.6. A ‘ = U – A
= Set of all triangle in a plane – Set of all triangle with at least the angle different from 60°.
= Set of all triangle with each angle 60°.
A´ = set of all equilateral triangle.
Q7. Fill in the blanks to make each of the following a true statement :
(i) A ∪ A ‘= . . . (ii) ϕ’∩ A = . . .
(iii) A ∩ A ‘= . . . (iv)U ‘ ∩ A = . . .
A.7. (i)A ∪A ‘ = U
(ii) ϕ∩ A = U ∩ A = A.
(iii)A ∩ A ‘ = ϕ .
(iv)U ‘ ∩ A = ϕ ∩ A = ϕ .
Q1. If X and Y are two sets such that n( X ) = 17, n ( Y ) = 23 and n(X ∪ Y) = 38,find n(X ∩ Y).
A.1. Given, n (X)= 17
n (Y) = 23
n(X ∪Y)= 38.
So, n(X ∪ Y) = n(X) + n(Y) n(X ∩Y)
n(X ∩Y) = n(X) + n(Y) n(X ∪Y)
= 17 + 23 38.
= 2
Q2. If X and Y are two sets such that X ∪ Y has 18 elements, X has 8 elements and Y has 15 elements; how many elements does X ∩ Y have?
A.2. Given, n(X ∪Y) = 18.
n(X) = 8.n(Y) = 15.n(X ∩Y) = ?
Usingn(X ∩Y) = n(X) + n(Y) n(X ∪Y)
= 8 + 15 18.
= 5.
Q3. In a group of 400 people, 250 can speak Hindi and 200 can speak English. How many people can speak both Hindi and English?
A.3. Let H and E be set if people who speak Hindi and English respectively. there,
n(H) = 250, people speak Hindi n(E) = 200, people speak English
n(H ∪E) = 400, people speaks either Hindi or English
So, n(H ∩E) = n(H) + n(E) n(H ∩E)
= 250 + 200 400
= 50
So, 50 people can speak both Hindi and English.
Q4. If S and T are two sets such that S has 21 elements, T has 32 elements, and S ∩T has 11 elements, how many elements does S ∪ T have?
A.4. Given,n(S) = 21
n(T) = 32
n(S ∩T) = 11.
Using, n(S ∪T) = n(S) + n(T) n(S ∩T)
= 21 + 32 11
= 42.
Q5. If X and Y are two sets such that X has 40 elements, X ∪ Y has 60 elements and X ∩ Y has 10 elements, how many elements does Y have?
A5. Given, n(X) = 40
n(Y ∪Y) = 60.
n(X ∩Y) = 10.
n(Y) = ?
Using, n(X ∪Y) = n(X) + n(Y) n(X ∩Y)
60 = 40 + n(y) 10.
n(Y) = 60 40 + 10
n(Y) = 30.
Q6. In a group of 70 people, 37 like coffee, 52 like tea and each person likes at least one of the two drinks. How many people like both coffee and tea?
A.6. Let A and B but the set of people who likes coffee and tea.
Then, n(A) = 37. no. of people who like coffee
n(B) = 52, no. of people who like tea.
As each person likes at least one of the two drink,
n(A ∪B) = 70.
So using, n(A ∪B) = n(A) + n(B) n (A ∩B)
n(A ∩B) = n(A) + n(B) n(A ∪B)
= 37 + 52 70
= 89 70
= 19
So, 19 people likes both coffee and tea.
Q7. In a group of 65 people, 40 like cricket, 10 like both cricket and tennis. How many like tennis only and not cricket? How many like tennis?
A.7. Let C and T be the set of people who likes cricket and tennis respectively. Then,
n(C) = 40, people who likes cricket
n(C ∪T) = 65, people who likes either cricket or tennis
and n(C ∩T) = 10, people who likes both
So, n(C ∪T) = n(C) + n(T) n(C ∩T)
65 = 40 + n(T) 10
n(T) = 35
So, 35 people likes tennis
And number of people who likes tennis only and not cricket
(TC) = n(T) n(C ∩T) = 35 10 = 25.
Q8. In a committee, 50 people speak French, 20 speak Spanish and 10 speak both Spanish and French. How many speak at least one of these two languages?
A.8. Let A and B be set of people who speaks Frenchand Spanish respectively. Then,
n(A) = 50, people speak French
n(B) = 20, people speak Spanish.
n(A ∩B) = 10, speaks both French& Spanish.
So, number of people who speaks at least one of these two languages
= n(A ∪B)
= n(A) + n(B) n(A ∩B)
= 50 + 20 10
= 60
