NCERT Solutions for Class 10 Maths Chapter 10, Circles, provide a comprehensive guide for students to understand concepts related to circles, including their properties, tangents, and theorems. This chapter delves into the basics of circles, covering key topics like the tangent to a circle, the number of tangents from a point outside the circle, and the theorem stating that the tangent at any point of a circle is perpendicular to the radius at that point. These solutions offer step-by-step explanations and examples that help students grasp complex ideas with ease, preparing them for both board exams and practical applications. Designed according to the CBSE syllabus, the solutions enable students to strengthen their problem-solving skills and gain a solid understanding of circle geometry.
NCERT Solutions Maths Ch-10 Circles
We try to teach you all Questions in easy way. We solve all chapter wise sums of maths textbook. In every chapter include NCERT solutions. For solutions of Exercise 10.1 click on Tabs :
1. How many tangents can a circle have?
Answer:
There can be infinite tangents to a circle. A circle is made up of infinite points which are at an equal distance from a point. Since there are infinite points on the circumference of a circle, infinite tangents can be drawn from them.
2. Fill in the blanks:
(i) A tangent to a circle intersects it in …………… point(s).
(ii) A line intersecting a circle in two points is called a ………….
(iii) A circle can have …………… parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called …………
Answer:
(i) A tangent to a circle intersects it in one point(s).
(ii) A line intersecting a circle in two points is called a secant.
(iii) A circle can have two parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called the point of contact.
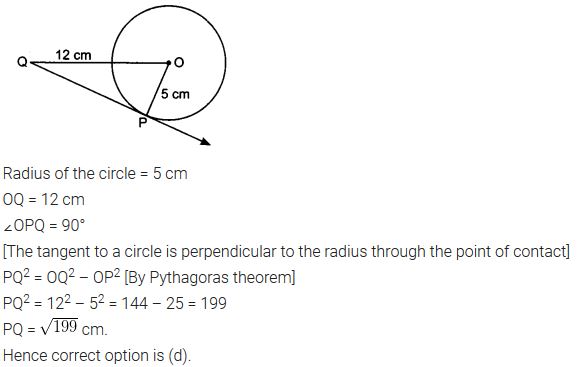
3. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at
a point Q so that OQ = 12 cm. Length PQ is :
(A) 12 cm
(B) 13 cm
(C) 8.5 cm
(D) √119 cm
Solution:
Question 4.
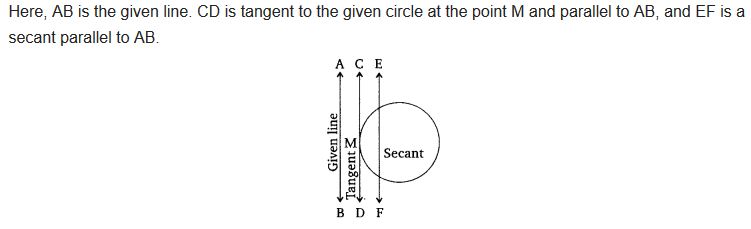
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Solution:
In Q.1 to 3 choose the correct option and give justification.
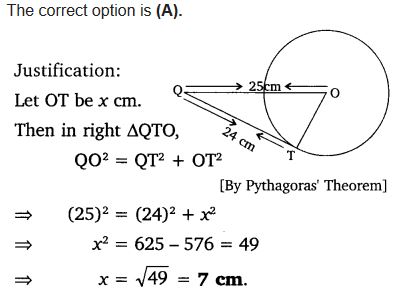
Question 1.
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(a) 7 cm
(b) 12 cm
(c) 15 cm
(d) 24.5 cm
Solution:
Question 2.
In figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to
(a) 60°
(b) 70°
(c) 80°
(d) 90°
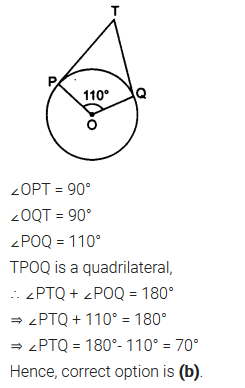
Question 3.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠POA is equal to
(a) 50°
(b) 60°
(c) 70°
(d) 80°
Solution:

Question 4.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Solution:
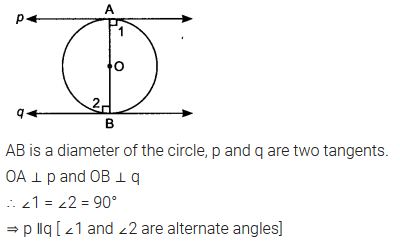
Question 5.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Solution:
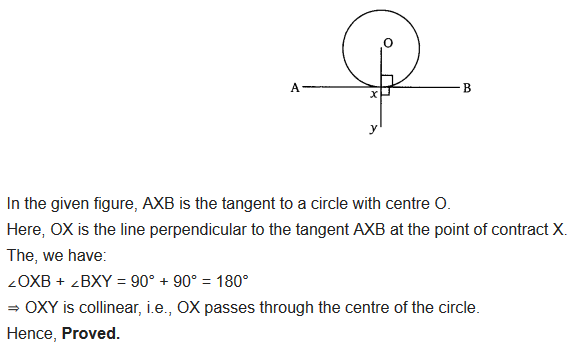
Question 6.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Solution:
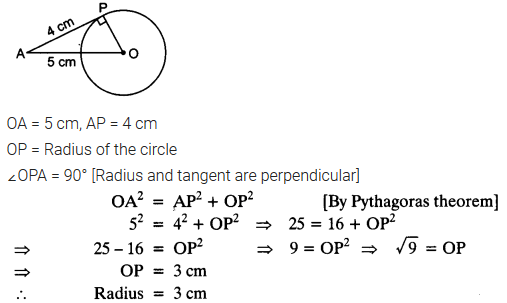
Question 7.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution:
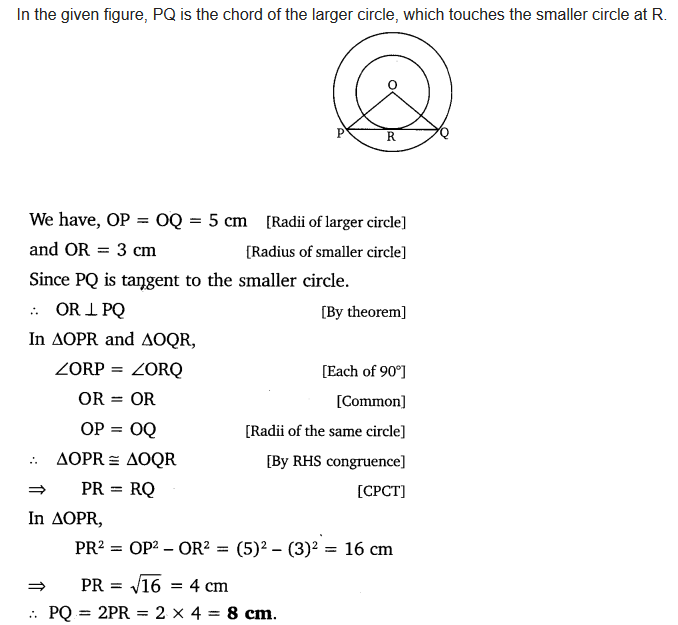
Question 8.
A quadrilateral ABCD is drawn to circumscribe a circle (see figure). Prove that AB + CD = AD + BC.
Solution:
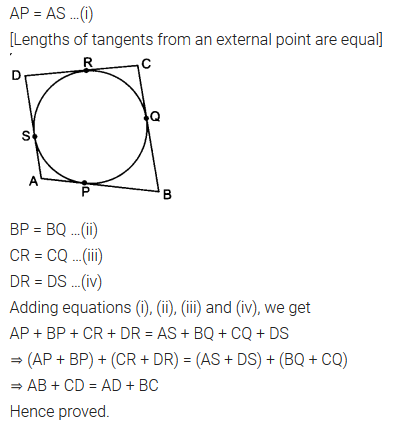
Question 9.
In figure, XY and X’Y’ are two parallel tangents to a circle , x with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°.

Solution:

Question 10.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
Solution:
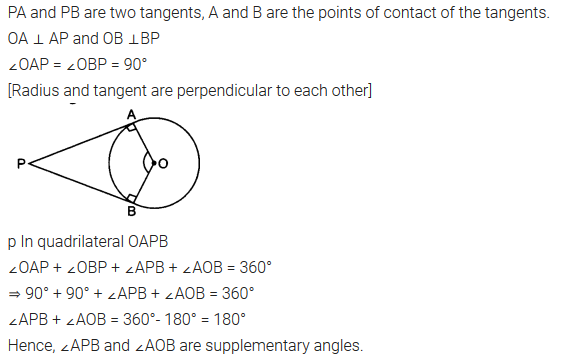
Question 11.
Prove that the parallelogram circumscribing a circle is a rhombus.
Solution:
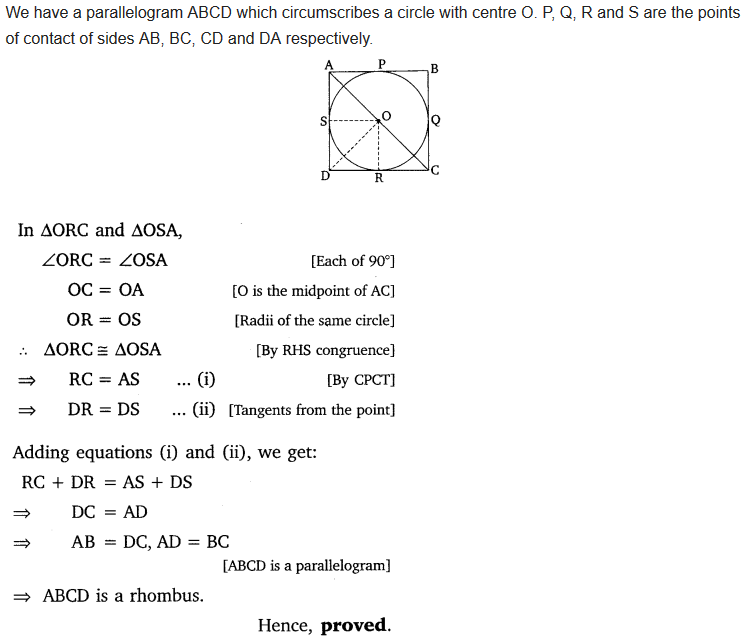
Question 12.
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see figure). Find the sides AB and AC.
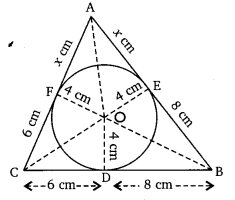
Solution:
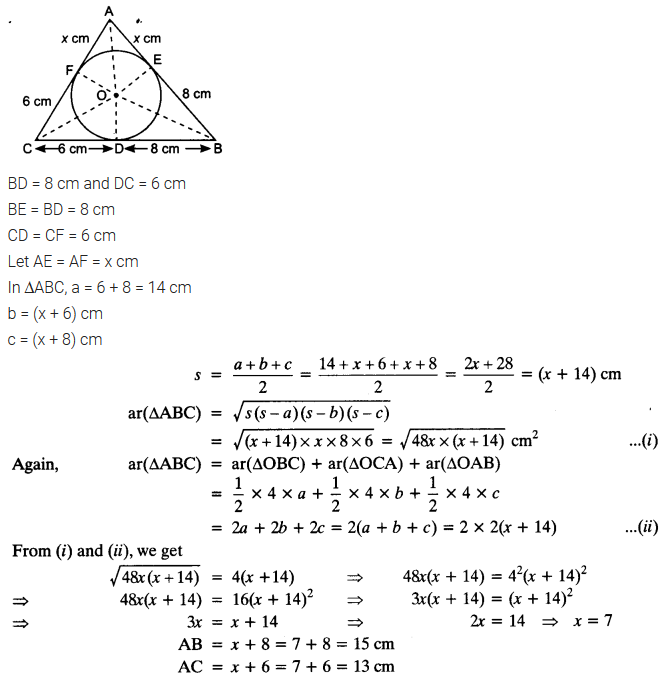
Question 13.
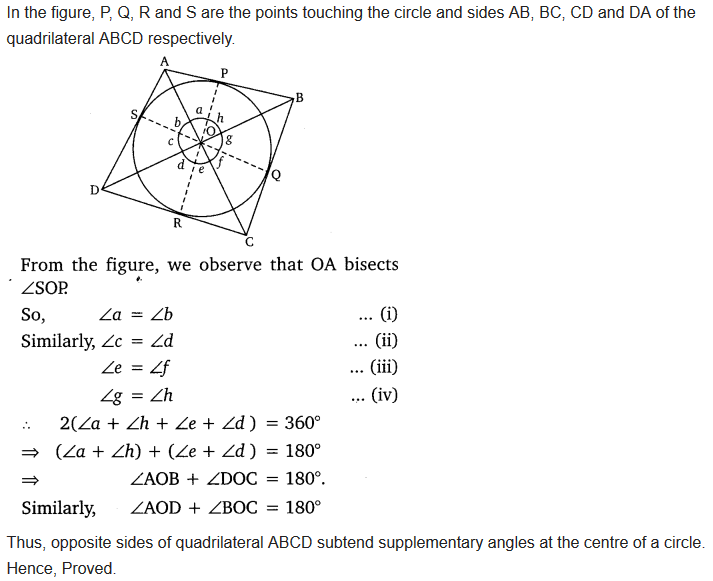
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution: