Chapter 15 of the NCERT Class 9 Mathematics textbook covers the topic of Probability. It introduces students to the basic concepts of probability, emphasizing the idea of chance and uncertainty in events. The chapter begins with the definition of probability as a measure of the likelihood of an event occurring, which is expressed as a number between 0 and 1.
The chapter includes various examples, such as rolling dice and drawing cards, to illustrate how to determine favorable outcomes and total outcomes. It also discusses the difference between theoretical probability and experimental probability, highlighting the importance of conducting experiments to observe outcomes in real-life scenarios.
Additionally, the chapter explains the concept of complementary events and how to calculate the probability of the occurrence of at least one of several events. Exercises at the end of the chapter help reinforce these concepts, allowing students to practice problem-solving skills related to probability. Overall, this chapter serves as a foundational introduction to the principles of probability, preparing students for more advanced topics in mathematics.
NCERT Solutions of Class 9th Chapter 15 Probability Exercise 15.1
We try to teach you all Questions in easy way. We solve all chapter wise sums of maths textbook. In every chapter include NCERT solutions. For solutions of Exercise 15.1, click on Tabs :
1. In a cricket match, a batswoman hits a boundary 6 times out of 30 balls she plays. Find the probability that she did not hit a boundary.
Solution:
According to the question,
Total number of balls = 30
Numbers of boundary = 6
Number of time bats woman didn’t hit boundary = 30 – 6 = 24
Probability she did not hit a boundary = 24/30 = 4/5
2. 1500 families with 2 children were selected randomly, and the following data were recorded:

Compute the probability of a family, chosen at random, having
(i) 2 girls (ii) 1 girl (iii) No girl
Also check whether the sum of these probabilities is 1.
Solution:
Total numbers of families = 1500
(i) Numbers of families having 2 girls = 475
Probability = Numbers of families having 2 girls/Total numbers of families
= 475/1500 = 19/60
(ii) Numbers of families having 1 girls = 814
Probability = Numbers of families having 1 girls/Total numbers of families
= 814/1500 = 407/750
(iii) Numbers of families having 2 girls = 211
Probability = Numbers of families having 0 girls/Total numbers of families
= 211/1500
Sum of the probability = (19/60)+(407/750)+(211/1500)
= (475+814+211)/1500
= 1500/1500 = 1
Yes, the sum of these probabilities is 1.
3. Refer to Example 5, Section 14.4, Chapter 14. Find the probability that a student of the class was born in August.
Solution:
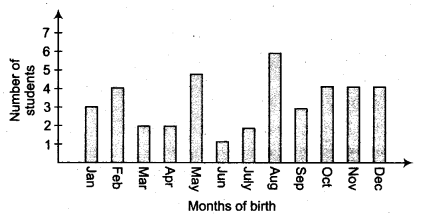
Total numbers of students in the class = 40
Numbers of students born in August = 6
The probability that a student of the class was born in August, = 6/40 = 3/20
4. Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes:

If the three coins are simultaneously tossed again, compute the probability of 2 heads coming up.
Solution:
Number of times 2 heads come up = 72
Total number of times the coins were tossed = 200
∴, the probability of 2 heads coming up = 72/200 = 9/25
5. An organisation selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family. The information gathered is listed in the table below:
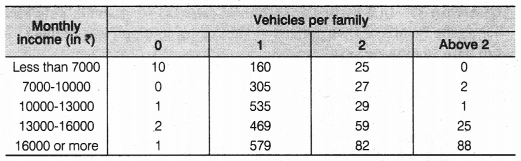
Suppose a family is chosen. Find the probability that the family chosen is
(i) earning ₹10000 – 13000 per month and owning exactly 2 vehicles.
(ii) earning ₹16000 or more per month and owning exactly 1 vehicle.
(iii) earning less than ₹7000 per month and does not own any vehicle.
(iv) earning ₹13000 – 16000 per month and owning more than 2 vehicles.
(v) owning not more than 1 vehicle.
Solution:
Total number of families = 2400
(i) Numbers of families earning ₹10000 –13000 per month and owning exactly 2 vehicles = 29
∴, the probability that the family chosen is earning ₹10000 – 13000 per month and owning exactly 2 vehicles = 29/2400
(ii) Number of families earning ₹16000 or more per month and owning exactly 1 vehicle = 579
∴, the probability that the family chosen is earning₹16000 or more per month and owning exactly 1 vehicle = 579/2400
(iii) Number of families earning less than ₹7000 per month and does not own any vehicle = 10
∴, the probability that the family chosen is earning less than ₹7000 per month and does not own any vehicle = 10/2400 = 1/240
(iv) Number of families earning ₹13000-16000 per month and owning more than 2 vehicles = 25
∴, the probability that the family chosen is earning ₹13000 – 16000 per month and owning more than 2 vehicles = 25/2400 = 1/96
(v) Number of families owning not more than 1 vehicle = 10+160+0+305+1+535+2+469+1+579
= 2062
∴, the probability that the family chosen owns not more than 1 vehicle = 2062/2400 = 1031/1200
6. A teacher wanted to analyse the performance of two sections of students in a mathematics test of 100 marks. Looking at their performances, she found that a few students got under 20 marks and a few got 70 marks or above. So she decided to group them into intervals of varying sizes as follows
0 – 20, 20 – 30, …, 60 – 70, 70 – 100. Then she formed the following table
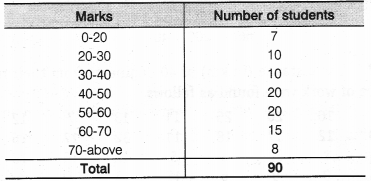
(i) Find the probability that a student obtained less than 20% in the mathematics test.
(ii) Find the probability that a student obtained marks 60 or above.
Solution:
Total number of students = 90
(i) Number of students who obtained less than 20% in the mathematics test = 7
∴, the probability that a student obtained less than 20% in the mathematics test = 7/90
(ii) Number of students who obtained marks 60 or above = 15+8 = 23
∴, the probability that a student obtained marks 60 or above = 23/90
7. To know the opinion of the students about the subject statistics, a survey of 200 students was conducted. The data is recorded in the following table.

Find the probability that a student chosen at random
(i) likes statistics,
(ii) does not like it.
Solution:
Total number of students = 135+65 = 200
(i) Number of students who like statistics = 135
, the probability that a student likes statistics = 135/200 = 27/40
(ii) Number of students who do not like statistics = 65
∴, the probability that a student does not like statistics = 65/200 = 13/40
8. The distance (in km) of 40 engineers from their residence to their place of work were found as follows

What is the empirical probability that an engineer lives:
(i) less than 7 km from her place of work?
(ii) more than or equal to 7 km from her place of work?
(iii) Within ½ km from her place of work?
Solution:
The distance (in km) of 40 engineers from their residence to their place of work were found as follows:
5 3 10 20 25 11 13 7 12 31 19 10 12 17 18 11 3 2
17 16 2 7 9 7 8 3 5 12 15 18 3 12 14 2 9 6
15 15 7 6 12
Total numbers of engineers = 40
(i) Number of engineers living less than 7 km from their place of work = 9
,the probability that an engineer lives less than 7 km from her place of work = 9/40
(ii) Number of engineers living more than or equal to 7 km from their place of work = 40-9 = 31
,probability that an engineer lives more than or equal to 7 km from her place of work = 31/40
(iii) Number of engineers living within ½ km from their place of work = 0
∴, the probability that an engineer lives within ½ km from her place of work = 0/40 = 0
9. Activity : Note the frequency of two-wheelers, three-wheelers and four-wheelers going past during a time interval, in front of your school gate. Find the probability that any one vehicle out of the total vehicles you have observed is a two-wheeler.
Solution:
The question is an activity to be performed by the students.
Hence, perform the activity by yourself and note down your inference.
10. Activity : Ask all the students in your class to write a 3-digit number. Choose any student from the room at random. What is the probability that the number written by her/him is divisible by 3? Remember that a number is divisible by 3, if the sum of its digits is divisible by 3.
Solution:
The question is an activity to be performed by the students.
Hence, perform the activity by yourself and note down your inference.
11. Eleven bags of wheat flour, each marked 5 kg, actually contained the following weights of flour (in kg):
4.97 5.05 5.08 5.03 5.00 5.06 5.08 4.98 5.04 5.07 5.00
Find the probability that any of these bags chosen at random contains more than 5 kg of flour.
Solution:
Total number of bags present = 11
Number of bags containing more than 5 kg of flour = 7
∴, the probability that any of the bags chosen at random contains more than 5 kg of flour = 7/11
12. In Q.5, Exercise 14.2, you were asked to prepare a frequency distribution table, regarding the concentration of sulphur dioxide in the air in parts per million of a certain city for 30 days. Using this table, find the probability of the concentration of sulphur dioxide in the interval 0.12-0.16 on any of these days.
The data obtained for 30 days is as follows:
0.03 0.08 0.08 0.09 0.04 0.17 0.16 0.05 0.02 0.06 0.18 0.20 0.11 0.08 0.12 0.13 0.22 0.07 0.08 0.01 0.10 0.06 0.09 0.18 0.11 0.07 0.05 0.07 0.01 0.04
Solution:
Total number of days in which the data was recorded = 30 days
Numbers of days in which sulphur dioxide was present in between the interval 0.12-0.16 = 2
∴, the probability of the concentration of sulphur dioxide in the interval 0.12-0.16 on any of these days = 2/30 = 1/15
13. In Q.1, Exercise 14.2, you were asked to prepare a frequency distribution table regarding the blood groups of 30 students of a class. Use this table to determine the probability that a student of this class, selected at random, has blood group AB.
The blood groups of 30 students of Class VIII are recorded as follows:
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O, A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O.
Solution:
Total numbers of students = 30
Number of students having blood group AB = 3
∴, the probability that a student of this class, selected at random, has blood group AB = 3/30 = 1/10
