Number Patterns:
- Understanding sequences and series.
- Identifying arithmetic and geometric progressions.
Divisibility Rules:
- Rules for divisibility by 2, 3, 4, 5, 6, 9, and 10.
- How to check if a number is divisible by another without performing long division.
Prime and Composite Numbers:
- Definition and properties of prime numbers (numbers with exactly two distinct positive divisors).
- Composite numbers (numbers with more than two positive divisors).
Even and Odd Numbers:
- Characteristics of even (divisible by 2) and odd numbers (not divisible by 2).
- Operations involving even and odd numbers.
Magic Squares and Puzzles:
- Introduction to magic squares and number puzzles.
- Solving problems related to number arrangements.
Algebraic Expressions:
- Basic manipulation of algebraic expressions.
- Understanding how numbers can represent variables in equations
NCERT Solutions of Class 8th Chapter 11 Mensuration Exercise 16.1, 16.2
We try to teach you all Questions in easy way. We solve all chapter wise sums of maths textbook. In every chapter include NCERT solutions. For solutions of Exercise 16.1 and 16.2
Find the values of the letters in each of the following and give reasons for the steps involved.
Question 1.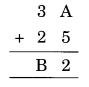
Solution:
Question 2.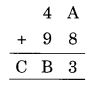
Solution: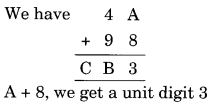

Question 3.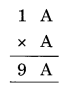
Solution: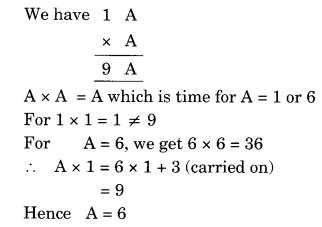
Question 4.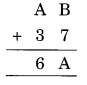
Solution: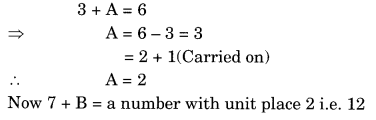
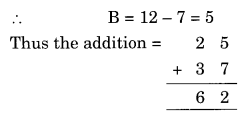
Question 5.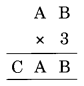
Solution:
3 × B = B
⇒ B = D
3 × A = CA
⇒ 3 × 5 = 15
Thus A = 5 and C = 1
Hence A = 5, B = 0 and C = 1
Question 6.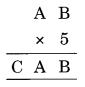
Solution:
5 × B = B
⇒ B = 0 or 5
5 × A = CA
5 × 5 = 25
Only possible when B = 0
Thus A = 5 and C = 2
Hence A = 5, B = 0 and C = 2
Question 7.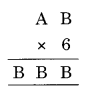
Solution:
B × 6 = B
6 × 4 = 24 → B = 4 and 2 is carried to
6 × A = BB
⇒ 6 × 7 = 42 + 2 (carried on) = 44
Thus B = 7
Hence A = 7 and B = 4
Question 8.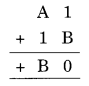
Solution:
1 + B = 0
1 + 9 = 10 → unit digit is 0 and 1 is carried to A
+ 1 +1 (carried on) = B = 9
A + 2 = 9 ⇒ A = 9 – 2 = 7
Hence A = 7 and B = 9
Question 9.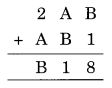
Solution:
B + 1 = 8 ⇒ B = 8 – 1 = 7
A + B = a number with unit digit 1
A + B = 11
⇒ A + 7 = 11
⇒ A = 11 – 7 = 4 (1 Carried to)
Now 1 carried on + 2 + A = B
3 + A = 7
⇒ A = 7 – 3 = 4
Hence A = 4, B = 7
Question 10.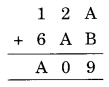
Solution:
9 = A + B
9 = 1 + 8 or 2 + 7 or 3 + 6 or 4 + 5 or 8 + 1 or 7 + 2 or 6 + 3 or 5 + 4 or 0 + 9 or 9 + 0
Now 0 is required at unit place
2 + A = 10
⇒ A = 10 – 2 = 8
B = 9 – 8 = 1
1 + 6 + 1 (carried on) = A = 8
Hence A = 8 and B = 1
Question 1.
If 21y5 is a multiple of 9, where y is a digit, what is the value of y?
Solution:
A number is divisible by 9 if the sum of its digits is also divisible by 9.
Sum of the digits of 21y5 = 2 + 1 +y + 5 = 8 + y
(8 + y) ÷ 9 = 1
⇒ 8 + y = 9
⇒ y = 9 – 8 = 1
Hence, the required value of y = 1.
Question 2.
If 31z5 is a multiple of 9, where z is a digit, what is the value of z?
Solution:
A number is a multiple of 9 when the sum of its digits is also divisible by 9.
Sum of the digits of 31z5 = 3 + 1 + z + 5
3 + 1 + 2 + 5 = 9k where k is an integer.
For k = 1,
3 + 1 + z + 5 = 9
⇒ z = 9 – 9 = 0
For k = 2,
3 + 1 + z + 5 = 18
⇒ z = 18 – 9 = 9
k = 3 is not possible because 3 + 1 + z + 5 = 27
⇒ z = 27 – 9 = 18 which is not a digit.
Hence the required value of z is 0 or 9
Question 3.
If 24x is a multiple of 3, where x is a digit, what is the value of x?
Solution:
Since 24x is a multiple of 3, the sum of digits 6 + x is a multiple of 3; so 6 + x is one of these numbers; 0, 3, 6, 12, 15, 18, ……..
6 + x = 3k where k is any integer.
For k = 0,
6 + x = 3 × 0
⇒ 6 + x = 0
x = -6. Not possible
For k = 1,
6 + x = 3 × 1
⇒ 6 + x = 3
⇒ x = 3 – 6 = -3. Not possible
For k = 2,
6 + x = 3 × 2
⇒ 6 + x = 6
⇒ x = 6 – 6 = 0
2 + 4 + 0 = 6 multiple of 3
For k = 3,
6 + x = 3 × 3
⇒ x = 9 – 6 = 3
2 + 4 + 3 = 9 multiple of 3
For k = 4,
6 + x = 3 × 4
⇒ 6 + x = 12
⇒ x = 12 – 6 = 6
2 + 4 + 6 = 12 which is multiple of 3
For k = 5,
6 + x = 3 × 5
⇒ x = 15 – 6 = 9
2 + 4 + 9 = 15 which is multiple of 3
For k = 6,
6 + x = 3 × 6
⇒ x = 18 – 6 = 12 not possible as x is digit
Hence the required values of x are 0, 3, 6 or 9.
Question 4.
If 31z5 is a multiple of 3, where z is a digit, what might be the value of z?
Solution:
A number is a multiple of 3 if the sum of its digits is divisible by 3.
3 + 1 + z + 5 = 3k where k is an integer
⇒ 9 + z = 3k
⇒ z = 3k – 9
Here, k = 0, 1, 2 is not possible as z is a digit of the number.
For k = 3,
z = 3 × 3 – 9 = 9 – 9 = 0
9 + 0 = 9 multiple of 3
For k = 4,
z = 3 × 4 – 9 = 12 – 9 = 3
9 + 3 = 12 multiple of 3
For k = 5,
z = 3 × 5 – 9 = 15 – 9 = 6
9 + 6 = 15 multiple of 3
For k = 6,
z = 3 × 6 – 9 = 18 – 9 = 9
9 + 9 = 18 multiple of 3
For k = 7,
z = 3 × 7 – 9 = 21 – 9 = 12 not possible as z is a digit
Hence, the required values of 2 are 0, 3, 6 and 9.
