Chapter 2 of the NCERT Maths textbook for Class 11, titled Relations and Functions, introduces two fundamental concepts in mathematics that are foundational for higher studies. A relation is a way of associating elements of one set with elements of another set, or within the same set. It is expressed as a collection of ordered pairs, where each pair contains an element from the first set and one from the second set. A function, which is a special type of relation, associates each element from one set (called the domain) to exactly one element of another set (called the range). The chapter delves into types of relations such as reflexive, symmetric, transitive, and antisymmetric, and explores the different types of functions, including one-to-one (injective), onto (surjective), and bijective functions. Understanding these concepts is crucial for solving problems involving mappings, domains, and ranges, and is the building block for studying more complex mathematical topics.
NCERT Solutions Maths Ch-2 Relations and Functions for Class 11th
NCERT Solutions of Class 11th Chapter2 Relations and Functions Exercises

Q2. If the set A has 3 elements and the set B = {3, 4, 5}, then find the number of elements in (A×B).
A.2. Given, n(A) = 3
n(B) = 3 or B = {3,4,5}
So, number of elements in A× B = n(A× B) = n(A)× n(B) = 3 ×3 = 9.
Q3. If G = {7, 8} and H = {5, 4, 2}, find G × H and H × G.
A.3. Given, G = {7, 8} and H = {5, 4, 2}
By the definition of the Cartesian product,
G ×H = {(x, y): x∈G and y = ∈ H}
= {((7, 5), (7, 4), (7, 2), (8, 5),(8,4), (8,2)}
H× G = {(x, y): x∈ H and y ∈G}
= {(5, 7), (5, 8), (4,7), (4, 8), (2, 7), (2,8)}
Q4. State whether each of the following statements are true or false. If the statement is false, rewrite the given statement correctly.
(i) If P = {m, n} and Q = { n, m}, then P × Q = {(m, n),(n, m)}.
(ii) If A and B are non-empty sets, then A × B is a non-empty set of ordered pairs (x, y) such that x ∈ A and y ∈ B.
(iii) If A = {1, 2}, B = {3, 4}, then A × ( B ∩ ϕ ) = ϕ .
A.4. (i) False. Here P = {m, n}, n(p)=2
Q = {n, m}, n(Q)=2
n(P× Q) = n(P)× n(Q) = 2× 2 = 4.
So, P ×Q = {((m, n),(m, m),(n, n),(n, m)}
(ii) True.
(iii) True. { A ×(B ∩ ϕ ) = A× ϕ . { ∵ B ∩ ϕ = ϕ }
= n(A) ×0 {∵ ϕ is empty set}
= ϕ
Q5. If A = {–1, 1}, find A × A × A.
A.5. Given, A = {1,1}
So, A× A = {(1,1),(1,1),(1,1),(1,1)}
A ×A ×A = {(1,1),(1,1),(1,1),(1,1)} ×{1,1}
= {(1,1.1),(1, 1, 1),(1, 1, 1,),(1,1,1), (1,1,1), (1, 1,1), (1, 1,1), (1,1,1)}
Q6. If A × B = {(a, x),(a , y), (b, x), (b, y)}. Find A and B.
A.6. Given,
A ×B = {(a, x),(a, y),(b, x),(b, y)}
We know that,
A ×B = {(p, q); p ∈ A and q ∈ B}
So, A = {a, b} and B = {x, y}.
Q7. Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}. Verify that (i) A × (B∩ C) = (A × B)∩ (A × C). (ii) A × C is a subset of B × D.
A.7.Given,
A={1, 2}, B = {1,2,3,4}, C={5,6} and D={5,6,7,8}
(i)L.H. S = A ×(B∩ C) = {1,2} [{1,2,3,4} ∩{5,6}]
={1,2}× ϕ
= ϕ .
R.H.S = (A× B)∩ (A ×C)=[{1,2}×{1,2,3,4}]∩[{1,2} {5,6}]
=[{(1 , 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)]∩ [{1,5),(1,6),(2,5), (2,6)}]
= ϕ .
Hence, L.H.S= R.H.S.
(ii)A× C ={1, 2}× {5,6}
={(1,5),(1,6),(2,5),(2,6)}
B× D ={1,2,3,4} ×{5,6,7,8}
={(1,5),(1,6),(1,7),(1,8),(2,5),(2,6),(2,7),(2,8),(3,5),(3,6),(3,7),(3,8),(4,5),(4,6),(4,7),(4,8)}
As every element of A C is also an element of B× D.
A ×C ⊂ B ×D
Q8. Let A = {1, 2} and B = {3, 4}. Write A × B. How many subsets will A × B have? List them.
A.8. A Given, A={1,2}
B={3,4}
So, A× B={(1,3),(1,4),(2,3),(2, 4)}
i.e., n(A ×B)=4
A ×B will have subset =24=16.They are,
Φ,{(1,3)},{(1,4)},{(2, 3)},{(2,4)},{(1,3),(1,4)},{(1,3),(2,3)},
{(1,3),(2, 4)},{(1,4),(2, 3)},{(1,4),(2, 4)}, {(2,3),(2, 4)},
{(1,3),(1,4),(2, 3)},{(1,3),(1,4),(2,4)}, {(1,3),(2,3),(2, 4)},{(1,4),(2,3),(2,4)},
and {(1,3),(1,4),(2,3),(2,4)}
Q9. Let A and B be two sets such that n(A) = 3 and n(B) = 2. If (x, 1), (y, 2), (z, 1) are in A × B, find A and B, where x, y and z are distinct elements.
A.9. Given, n(A)=3
n(B)= 2
So, n(Ax B)=n(A).n(B)=3x 2=6
as (x, 1),(y, 2),(z, 1) ∈Ax B={(x, y), x∈Aand y∈B}.
A={x, y, z} and B={1,2}
As n(A) = 3as n(B) = 2
Q10. The Cartesian product A × A has 9 elements among which are found (–1, 0) and (0,1). Find the set A and the remaining elements of A × A.
A.10. Given, n(A × A)=9
n(A) ×n(A) = 9.
n(A)2 = 32.
n(A) = 3 .
And (–1,0),(0,1) ∈ A × A i.e., A × A = {(x, y), x ∈ A, y ∈ B}
⸫A={–1,0,1}
And A × A={–1,0,1} × {–1,0,1}
={(–1, –1),( –1,0),( –1,1),(0, –1),(0,0),(0,1),(1, –1),(1,0),(1,1)}
Q1. Let A = {1, 2, 3,…,14}. Define a relation R from A to A by R = {(x, y) : 3x – y = 0, where x, y ∈ A}. Write down its domain, co domain and range.
A.1. Given,A ={1,2,3, …, 14}
R ={(x, y): 3x – y = 0; x, y ∈ A}
={(x, y): 3x = y; x, y ∈ A}.
= {(1,3),(2,6),(3,9),(4,12)}
Domain of R is the set of all the first elements of the ordered pairs in R
So, domain of R={1,2,3,4}
Codomain of R is the whole set A.
So, codomain of R={1,2,3, …, 14}
Range of R is the set of all the second elements of the ordered pains in R.
So, range of R={3,6,9,12}
Q2. Define a relation R on the set N of natural numbers by R = {(x, y) : y = x + 5, x is a natural number less than 4; x, y ∈ N}. Depict this relationship using roster form. Write down the domain and the range.
A.2. Given,R ={(x, y): y = x + 5, x is a natural number less than 4; x, y ∈ N}
={(x, y): y = x + 5; x, y ∈ N and x < 4}.
={(1,1+5), (2,2+5), (3,3+5)}
={(1,6), (2,7), (3,8)}
So, domain of R = {1,2,3}
range of R = {6,7,8}
Q3. A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R from A to B by R = {(x, y): the difference between x and y is odd; x ∈ A, y ∈ B}. Write R in roster form.
A.3. Given,A={1,2,3,5}
B={4,6,9}
R={(x, y) : the difference of x & y is odd; x ∈ A, y ∈ B}.
={(x, y):|x – y| is odd and x ∈ A, y ∈ B}
={(1,4),(1,6),(2,9),(3,4),(3,6),(5,4),(5,6)}.
Q4. The Fig 2.7 shows a relationship between the sets P and Q. Write this relation
(i) in set-builder form (ii) roster form. What is its domain and range?
A.4. As R is a relation from set P to Q.
(i)R = {(x, y): x – 2 = y ; 5 ≤ x ≤ 7}
(ii)R = {(5,3),(6,4),(7,5)}
Domain of R={5,6,7}
range of R={3,4,5}
Q5. Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b): a , b ∈ A, b is exactly divisible by a}.
(i) Write R in roster form
(ii) Find the domain of R
(iii) Find the range of R.
A.5. Given, A={1,2,3,4,6}
R={(a, b): a, b ∈ A, b is exactly divisible by a}
(i)R={(1,1),(1,2),(1,3),(1,4),(1,6),(2,2),(2,4),(2,6), (3,3),(3,6),(4,4),(6,6)}
(ii)Domain of R={1,2,3,4,6}
(iii)Range of R={1,2,3,4,6}
Q6. Determine the domain and range of the relation R defined by R = {(x, x + 5) : x ∈ {0, 1, 2, 3, 4, 5}}.
A.6. Given,R ={(x, x+5): x ∈ {0,1,2,3,4,5}}
={(0,0+5), (1,1+5), (2,2+5), (3,3+5), (4,4+5), (5,5+5)}
={(0,5),(1,6),(2,7),(3,8),(4,9),(5,10)}
So, domain of R={0,1,2,3,4,5}
range of R={5,6,7,8,9,10}
Q7. Write the relation R = {(x,x3) : x is a prime number less than 10} in roster form.
A.7. GivenR={(x, x3) : x is a prime number less than 10}
R ={(x, x3) : x = 2,3,5,7}
={(2,23),(3,33),(5,53),(7,73)}
={(2,8),(3,27),(5,125),(7,343)}
Q8. Let A = {x, y, z} and B = {1, 2}. Find the number of relations from A to B.
A.8. Given, A={x, y, z}so, n(A)=3
B={1,2} so n(B)=2
⸫ n(A × B)=n(A) ×n(B)=3 × 2=6
Hence, no. of relation from A to B=Number of subsets of A × B
=26
=64.
Q9. Let R be the relation on Z defined by R = {(a,b): a, b ∈ Z, a – b is an integer}. Find the domain and range of R.
A.9. Given,R={(a, b): a, b ∈ z and a – b is an integer}
We know that, the difference of two integers is also an integer.
R={(a, b): a – b ∈ z & a, b ∈ z}
Domain of R=Z.
Range of R= Z.
Q1. Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.
(i) {(2,1), (5,1), (8,1), (11,1), (14,1), (17,1)}
(ii) {(2,1), (4,2), (6,3), (8,4), (10,5), (12,6), (14,7)}
(iii) {(1,3), (1,5), (2,5)}.
A.1. (i)Domain of the given relation ={2,5,8,11,14,17}
Since every element of the domain has one and only one image, the given relation is a fxn.
So, domain ={2,5,8,11,14,17}
range ={1}
(ii)Domain of the given relation ={2,4,6,8,10,12,14}
Since every element of the domain has one and only one image, the given relation is a fxn.
So, domain = {2, 4, 6, 8, 10, 12, 14}
range ={1,2,3,4,5,6,7}
(iii)Domain of the given relation ={1,2}
As element 1 has more than one image i.e., 3 and 5, the given relation is not a fxn.

Q3. A function f is defined by f(x) = 2x –5. Write down the values of
(i) f (0), (ii) f (7), (iii) f (–3).
A.3. Give, f(x) = 2x – 5.
(i)f(0)=(2 × 0) –5=0 – 5= –5
(ii)f(7)=(2 × 7) –5=14 – 5=9
(iii)f(–3)=2 ×(–3) –5= –6 – 5= –11.
Q4. The function ‘t’ which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by t(C) = 9 C / 5 + 3 2 .
Find (i) t(0) (ii) t(28) (iii) t(–10) (iv) The value of C, when t(C) = 212.
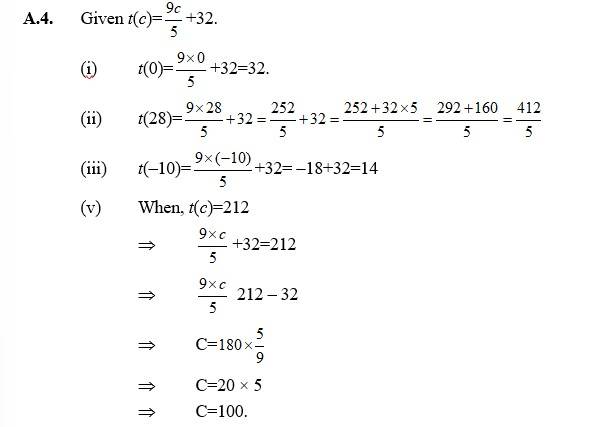
Q5. Find the range of each of the following functions.
(i) f (x) = 2 – 3x, x ∈ R, x > 0.
(ii) f (x) = x2+ 2, x is a real number.
(iii) f (x) = x, x is a real number.
A.5. (i)f(x)=2 – 3x, x ∈ R, x>0.
Given, x>0
3x>3 × 0
3x>0
(–1) × 3x<(–1) × 0.
–3x<0
2 – 3x<0+2
2 – 3x<2
i.e., f(x) < 2
Hene, range of f(x) = (– ꝏ, 2)
(ii)Given, f(x) = x2+2, x is a real number.
Since, x is a real number,
x2 ≥ 0 (x2=0 for x=0)
x2+2 ≥ 0+2
x2+2 ≥ 2
f(x) ≥ 2
⸫Range of f(x) = [2, ꝏ)
(iii)Given, f(x) = x, x is a real number.
As, f(x) = x, the range of f(x) is also real.
i.e., Range of f(x) = R.
