Here’s a summary of the key concepts and solutions for Chapter 5: Data Handling from the NCERT Class 8 Maths textbook.
Data: Information collected for analysis. Data can be quantitative (numerical) or qualitative (categorical).
Organizing Data: Data can be organized in various ways, including:
- Tables: To present data clearly.
- Bar Graphs: Useful for comparing quantities.
- Histograms: For showing frequency distribution of continuous data.
- Pie Charts: To represent parts of a whole.
Mean, Median, Mode:
- Mean: Average of a data set. Calculated by adding all the values and dividing by the number of values.
- Median: The middle value when data is arranged in ascending or descending order.
- Mode: The value that appears most frequently in a data set.
Range: The difference between the highest and lowest values in a data set.
Probability: The likelihood of an event occurring, calculated as the ratio of favorable outcomes to total outcomes.
NCERT Solutions of Class 8th Chapter 5 Data Handling Exercise 5.1, 5.2 and 5.3
We try to teach you all Questions in easy way. We solve all chapter wise sums of maths textbook. In every chapter include NCERT solutions. For solutions of Exercise 5.1, 5.2 and 5.3 click on Tabs :
Question 1.
For which of these would you use a histogram to show the data?
(i) The number of letters for different areas in a postman’s bag.
(ii) The height of competitors in an athletics meet.
(iii) The number of cassettes produced by 5 companies.
(iv) The number of passengers boarding trains from 7 a.m to 7 p.m at a station.
Give a reason for each.
Solution:
(i) The number of areas cannot be represented in class-intervals. So, we cannot use the histogram to show the data.
(ii) Height of competitors can be divided into intervals.
(iii) Companies cannot be divided into intervals.
(iv) Time for boarding the train can be divided into intervals.
Question 2.
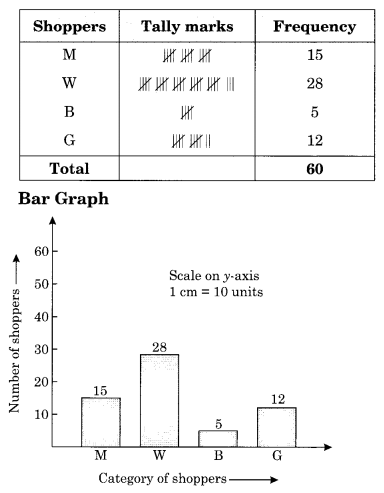
The shoppers who come to a departmental store are marked as: man (M), woman (W), boy (B) or girl (G). The following list gives the shoppers who came during the first hour in the morning.
W W W G B W W M G G M M W W W W
G B M W B G G M W W M M W W W
M W B W G M W W W W G W M M W
W M W G W M G W M M B G G W
Make a frequency distribution table using tally marks. Draw a bar graph to illustrate it.
Solution:
Question 3.
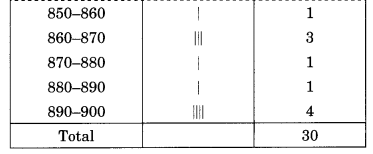
The weekly wages (in ₹) of 30 workers in a factory are:
830, 835, 890, 810, 835, 836, 869, 845, 898, 890,
820, 860, 832, 833, 855, 845, 804, 808, 812, 840,
885, 835, 835, 836, 878, 840, 868, 890, 806, 840
Using tally marks make a frequency table with intervals as 800-810, 810-820 and so on.
Solution:

Question 4.
Draw a histogram for the frequency table made for the data in Question 3, and answer the following questions:
(i) Which group has the maximum number of workers?
(ii) How many workers earn ₹ 850 and more?
(iii) How many workers earn less than ₹ 850?
Solution:
Refer to the frequency table of Question No. 3.
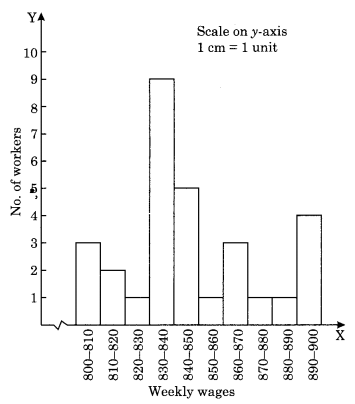
(i) Group 830-840 has the maximum number of workers, i.e., 9.
(ii) 10 workers earn equal and more than Rs. 850.
(iii) 20 workers earn less than Rs. 850.
Question 5.
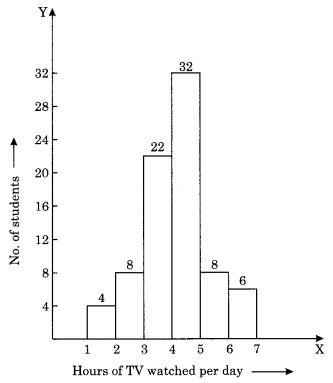
The number of hours for which students of a particular class watched television during holidays is shown through the given graph.
Answer the following questions.
(i) For how many hours did the maximum number of students watch TV?
(ii) How many students watched TV for less than 4 hours?
(iii) How many students spent more than 5 hours watching TV?
Solution:
(i) 32 is the maximum number of students who watched TV for 4 to 5 hours.
(ii) 4 + 8 + 22 = 34 students watched TV for less than 4 hours.
(iii) 8 + 6 = 14 students watched TV for more than 5 hours.
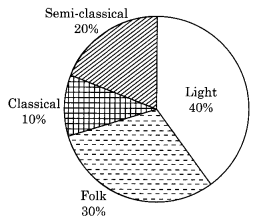
1. A survey was made to find the type of music that a certain group of young people liked in a city.
Adjoining pie chart shows the findings of this survey. From this pie chart, answer the following:
(i) If 20 people liked classical music, how many young people were surveyed?
(ii) Which type of music is liked by the maximum number of people?
(iii) If a cassette company were to make 1000 CD’s, how many of each type would they
make?
Solution:
(i) 10% represents 100 people.
⟹20% represents = (100×20)/10 = 200
∴, 200 people were surveyed.
(ii) Since 40% of the total people surveyed liked light music and no other form of song liked more than that, we can conclude that Light music is liked by the maximum number of people.
(iii) CD’s of classical music = (10 × 1000)/100 = 100
CD’s of semi-classical music = (20 × 1000)/100 = 200
CD’s of light music = (40 × 1000)/100 = 400
CD’s of folk music = (30 × 1000)/100 = 300
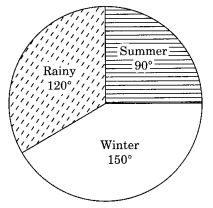
Question 2. A group of 360 people were asked to vote for their favorite season from the three
seasons rainy, winter and summer.
(i) Which season got the most votes?
(ii)Find the central angle of each sector.
(iii) Draw a pie chart to show this information

Solution:
(i) (i) Winter season got the most votes, i.e. 150
(ii) Central angle of summer season= (90×360)/360= 90o
Central angle of rainy season= (120×360)/360= 120o
Central angle of winter season= (150×360)/360= 150o
(iii) Pie chart
Question 3.
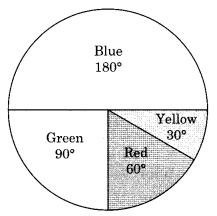
Draw a pie chart showing the following information. The table shows the colours preferred by a group of people.
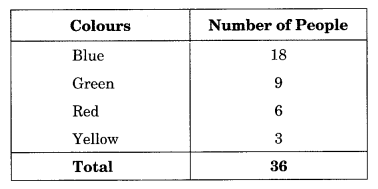
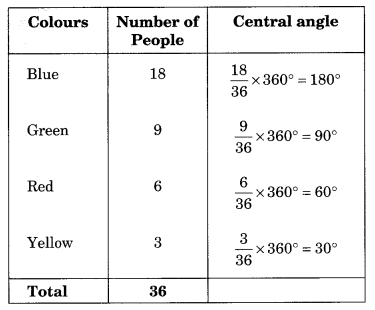
Solution:
Table to find the central angle of each sector
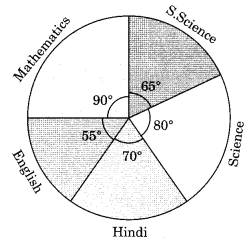
Question 4. The adjoining pie chart gives the marks scored in an examination by a student in Hindi, English, Mathematics, Social Science and Science. If the total marks obtained by the students were 540, answer the following questions.
(i) In which subject did the student score 105 marks?
(Hint: for 540 marks, the central angle = 360°. So, for 105 marks, what is the central angle?)
(ii) How many more marks were obtained by the student in Mathematics than in Hindi?
(iii) Examine whether the sum of the marks obtained in Social Science and Mathematics is more than that in Science and Hindi. (Hint: Just study the central angles).
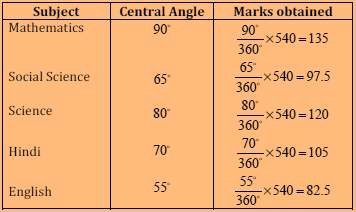
(i) The student scored 105 marks in Hindi.
(ii) Marks obtained in Mathematics = 135 Marks obtained in Hindi = 105 Difference = 135 – 105 = 30
Thus, 30 more marks were obtained by the student in Mathematics than in Hindi.
(iii) The sum of marks in Social Science and Mathematics = 97.5 + 135 = 232.5 The sum of marks in Science and Hindi = 120 + 105 = 225
∴, the sum of the marks in Social Science and Mathematics is more than that in Science and Hindi.
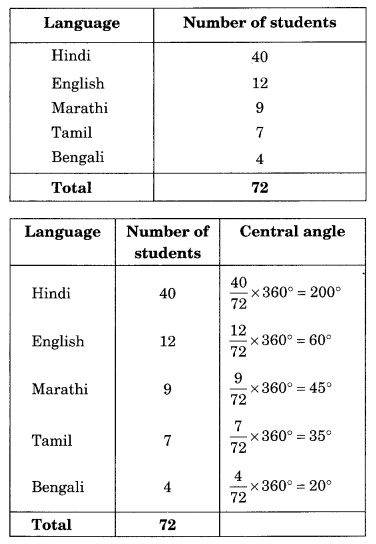
5. The number of students in a hostel, speaking different languages is given below. Display the data in a pie chart.
List the outcomes you can see in these experiments.
(a) Spinning a wheel (b) Tossing two coins together
Solution:
(a) There are four letters A, B, C and D in a spinning wheel. So there are 4 outcomes.
(b) When two coins are tossed together. There are four possible outcomes HH, HT, TH, TT.
2. When a die is thrown, list the outcomes of an event of getting
(i) (a) a prime number (b) not a prime number.
(ii) (a) a number greater than 5 (b) a number not greater than 5.
Solution:
(i) (a) Outcomes of event of getting a prime number are 2, 3 and 5.
(b) Outcomes of event of not getting a prime number are 1, 4 and 6.
(ii) (a) Outcomes of event of getting a number greater than 5 is 6.
(b) Outcomes of event of not getting a number greater than 5 are 1, 2, 3, 4 and 5.
3. Find the.
(a) Probability of the pointer stopping on D in (Question 1-(a)).
(b) Probability of getting an ace from a well shuffled deck of 52 playing cards.
(c) Probability of getting a red apple.
Solution:
(a) In a spinning wheel, there are five pointers A, A, B, C, D. So there are five
outcomes. Pointer stops at D which is one outcome.
So the probability of the pointer stopping on D = 1/5
(b) There are 4 aces in a deck of 52 playing cards. So there are four events of getting an ace.
So, probability of getting an ace = 4/52 = 1/13
(c) Total number of apples = 7
Number of red apples = 4
Probability of getting red apple = 4/7
4. Numbers 1 to 10 are written on ten separate slips (one number on one slip), kept in a box and mixed well. One slip is chosen from the box without looking into it. What is the probability of .
(i) getting a number 6?
(ii) getting a number less than 6? (iii) getting a number greater than 6? (iv)getting a 1-digit number?
Solution:
(i) Outcome of getting a number 6 from ten separate slips is one.
∴, probability of getting a number 6 = 1/10
(ii) Numbers less than 6 are 1, 2, 3, 4 and 5 which are five. So there are 5 outcomes.
∴, probability of getting a number less 6 =5/10 = ½
(iii)Number greater than 6 out of ten that are 7, 8, 9, 10. So there are 4 possible outcomes.
∴, probability of getting a number greater than 6 = 4/10 = 2/5
(iv) One digit numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9 out of ten.
∴, probability of getting a 1-digit number = 9/10
5. If you have a spinning wheel with 3 green sectors, 1 blue sector and 1 red sector, what is the probability of getting a green sector? What is the probability of getting a non-blue sector?
Solution:
A total of five sectors are present.
Out of the five sectors, three sectors are green.
∴, probability of getting a green sector = 3/5
Out of the five sectors, one sector is blue. Hence, Non-blue sectors = 5 – 1 = 4 sectors
∴, probability of getting a non-blue sector= 4/5
6. Find the probabilities of the events given in Question 2.
Solution:
When a die is thrown, there are total six outcomes, i.e., 1, 2, 3, 4, 5 and 6.
(i)
(a) 2, 3, 5 are the prime numbers. So there are 3 outcomes out of 6.
∴,probability of getting a prime number =3/6 = ½
(b) 1, 4, 6 are not the prime numbers. So there are 3 outcomes out of 6.
∴,probability of getting a prime number =3/6 = ½
(ii)
(c) Only 6 is greater than 5.
So there is one outcome out of 6.
∴,probability of getting a number greater than 5= 1/6
(d) Numbers not greater than 5 are 1, 2, 3, 4 and 5. So there are 5 outcomes out of 6.
∴,probability of not getting a number greater than 5= 5/6
