NCERT Solutions Maths Ch-8 Quadrilaterals for Class 9th
NCERT Solutions of Class 9th Chapter 8 Quadrilaterals Exercise 8.1, 8.2
We try to teach you all Questions in easy way. We solve all chapter wise sums of maths textbook. In every chapter include NCERT solutions. For solutions of Exercise 8.1, 8.2 click on Tabs :
Question 1.
The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.
Solution:
Let the angles of the quadrilateral be 3x, 5x, 9x and 13x.
∴ 3x + 5x + 9x + 13x = 360°
[Angle sum property of a quadrilateral]
⇒ 30x = 360°
⇒ x = 
∴ 3x = 3 x 12° = 36°
5x = 5 x 12° = 60°
9x = 9 x 12° = 108°
13a = 13 x 12° = 156°
⇒ The required angles of the quadrilateral are 36°, 60°, 108° and 156°.
Question 2.
If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Solution:
Let ABCD is a parallelogram such that AC = BD.
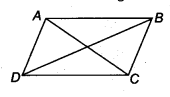
In ∆ABC and ∆DCB,
AC = DB [Given]
AB = DC [Opposite sides of a parallelogram]
BC = CB [Common]
∴ ∆ABC ≅ ∆DCB [By SSS congruency]
⇒ ∠ABC = ∠DCB [By C.P.C.T.] …(1)
Now, AB || DC and BC is a transversal. [ ∵ ABCD is a parallelogram]
∴ ∠ABC + ∠DCB = 180° … (2) [Co-interior angles]
From (1) and (2), we have
∠ABC = ∠DCB = 90°
i.e., ABCD is a parallelogram having an angle equal to 90°.
∴ ABCD is a rectangle.
Question 3.
Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Solution:
Let ABCD be a quadrilateral such that the diagonals AC and BD bisect each other at right angles at O.
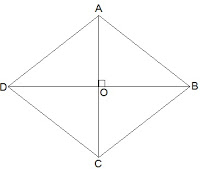
∴ In ∆AOB and ∆AOD, we have
AO = AO [Common]
OB = OD [O is the mid-point of BD]
∠AOB = ∠AOD [Each 90]
∴ ∆AQB ≅ ∆AOD [By,SAS congruency
∴ AB = AD [By C.P.C.T.] ……..(1)
Similarly, AB = BC .. .(2)
BC = CD …..(3)
CD = DA ……(4)
∴ From (1), (2), (3) and (4), we have
AB = BC = CD = DA
Thus, the quadrilateral ABCD is a rhombus.
Question 4.
Show that the diagonals of a square are equal and bisect each other at right angles.
Solution:
Let ABCD be a square such that its diagonals AC and BD intersect at O.
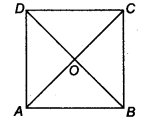
(i) To prove that the diagonals are equal, we need to prove AC = BD.
In ∆ABC and ∆BAD, we have
AB = BA [Common]
BC = AD [Sides of a square ABCD]
∠ABC = ∠BAD [Each angle is 90°]
∴ ∆ABC ≅ ∆BAD [By SAS congruency]
AC = BD [By C.P.C.T.] …(1)
(ii) AD || BC and AC is a transversal. [∵ A square is a parallelogram]
∴ ∠1 = ∠3
[Alternate interior angles are equal]
Similarly, ∠2 = ∠4
Now, in ∆OAD and ∆OCB, we have
AD = CB [Sides of a square ABCD]
∠1 = ∠3 [Proved]
∠2 = ∠4 [Proved]
∴ ∆OAD ≅ ∆OCB [By ASA congruency]
⇒ OA = OC and OD = OB [By C.P.C.T.]
i.e., the diagonals AC and BD bisect each other at O. …….(2)
(iii) In ∆OBA and ∆ODA, we have
OB = OD [Proved]
BA = DA [Sides of a square ABCD]
OA = OA [Common]
∴ ∆OBA ≅ ∆ODA [By SSS congruency]
⇒ ∠AOB = ∠AOD [By C.P.C.T.] …(3)
∵ ∠AOB and ∠AOD form a linear pair.
∴∠AOB + ∠AOD = 180°
∴∠AOB = ∠AOD = 90° [By(3)]
⇒ AC ⊥ BD …(4)
From (1), (2) and (4), we get AC and BD are equal and bisect each other at right angles.
Question 5.
Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Solution:
Let ABCD be a quadrilateral such that diagonals AC and BD are equal and bisect each other at right angles.
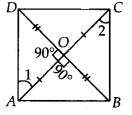
Now, in ∆AOD and ∆AOB, We have
∠AOD = ∠AOB [Each 90°]
AO = AO [Common]
OD = OB [ ∵ O is the midpoint of BD]
∴ ∆AOD ≅ ∆AOB [By SAS congruency]
⇒ AD = AB [By C.P.C.T.] …(1)
Similarly, we have
AB = BC … (2)
BC = CD …(3)
CD = DA …(4)
From (1), (2), (3) and (4), we have
AB = BC = CD = DA
∴ Quadrilateral ABCD have all sides equal.
In ∆AOD and ∆COB, we have
AO = CO [Given]
OD = OB [Given]
∠AOD = ∠COB [Vertically opposite angles]
So, ∆AOD ≅ ∆COB [By SAS congruency]
∴∠1 = ∠2 [By C.P.C.T.]
But, they form a pair of alternate interior angles.
∴ AD || BC
Similarly, AB || DC
∴ ABCD is a parallelogram.
∴ Parallelogram having all its sides equal is a rhombus.
∴ ABCD is a rhombus.
Now, in ∆ABC and ∆BAD, we have
AC = BD [Given]
BC = AD [Proved]
AB = BA [Common]
∴ ∆ABC ≅ ∆BAD [By SSS congruency]
∴ ∠ABC = ∠BAD [By C.P.C.T.] ……(5)
Since, AD || BC and AB is a transversal.
∴∠ABC + ∠BAD = 180° .. .(6) [ Co – interior angles]
⇒ ∠ABC = ∠BAD = 90° [By(5) & (6)]
So, rhombus ABCD is having one angle equal to 90°.
Thus, ABCD is a square.
Question 6.
Diagonal AC of a parallelogram ABCD bisects ∠A (see figure). Show that
(i) it bisects ∠C also,
(ii) ABCD is a rhombus.
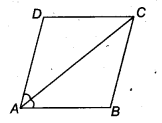
Solution:
(i) In ΔADC and ΔCBA,
AD = CB (Opposite sides of a parallelogram)
DC = BA (Opposite sides of a parallelogram)
AC = CA (Common Side)
, ΔADC ≅ ΔCBA [SSS congruency]
Thus,
∠ACD = ∠CAB by CPCT
and ∠CAB = ∠CAD (Given)
⇒ ∠ACD = ∠BCA
Thus,
AC bisects ∠C also.
(ii) ∠ACD = ∠CAD (Proved above)
⇒ AD = CD (Opposite sides of equal angles of a triangle are equal)
Also, AB = BC = CD = DA (Opposite sides of a parallelogram)
Thus,
ABCD is a rhombus.
Question 7.
ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
Solution:
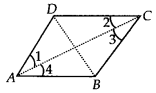
Solution:
Since, ABCD is a rhombus.
⇒ AB = BC = CD = DA
Also, AB || CD and AD || BC
Now, CD = AD ⇒ ∠1 = ∠2 …….(1)
[ ∵ Angles opposite to equal sides of a triangle are equal]
Also, AD || BC and AC is the transversal.
[ ∵ Every rhombus is a parallelogram]
⇒ ∠1 = ∠3 …(2)
[ ∵ Alternate interior angles are equal]
From (1) and (2), we have
∠2 = ∠3 …(3)
Since, AB || DC and AC is transversal.
∴ ∠2 = ∠4 …(4)
[ ∵ Alternate interior angles are equal] From (1) and (4),
we have ∠1 = ∠4
∴ AC bisects ∠C as well as ∠A.
Similarly, we can prove that BD bisects ∠B as well as ∠D.
Question 8.
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that
(i) ABCD is a square
(ii) diagonal BD bisects ∠B as well as ∠D.
Solution:
We have a rectangle ABCD such that AC bisects ∠A as well as ∠C.
i.e., ∠1 = ∠4 and ∠2 = ∠3 ……..(1)
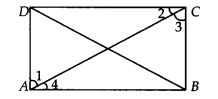
(i) Since, every rectangle is a parallelogram.
∴ ABCD is a parallelogram.
⇒ AB || CD and AC is a transversal.
∴∠2 = ∠4 …(2)
[ ∵ Alternate interior angles are equal]
From (1) and (2), we have
∠3 = ∠4
In ∆ABC, ∠3 = ∠4
⇒ AB = BC
[ ∵ Sides opposite to equal angles of a A are equal]
Similarly, CD = DA
So, ABCD is a rectangle having adjacent sides equal.
⇒ ABCD is a square.
(ii) Since, ABCD is a square and diagonals of a square bisect the opposite angles.
So, BD bisects ∠B as well as ∠D.
Question 9.
In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig. 8.20). Show that:
(i) ΔAPD ≅ ΔCQB
(ii) AP = CQ
(iii) ΔAQB ≅ ΔCPD
(iv) AQ = CP
(v) APCQ is a parallelogram
Solution:
(i) In ΔAPD and ΔCQB,
DP = BQ (Given)
∠ADP = ∠CBQ (Alternate interior angles)
AD = BC (Opposite sides of a parallelogram)
Thus, ΔAPD ≅ ΔCQB [SAS congruency]
(ii) AP = CQ by CPCT as ΔAPD ≅ ΔCQB.
(iii) In ΔAQB and ΔCPD,
BQ = DP (Given)
∠ABQ = ∠CDP (Alternate interior angles)
AB = CD (Opposite sides of a parallelogram)
Thus, ΔAQB ≅ ΔCPD [SAS congruency]
(iv) As ΔAQB ≅ ΔCPD
AQ = CP [CPCT]
(v) From the questions (ii) and (iv), it is clear that APCQ has equal opposite sides and also has equal and opposite angles. , APCQ is a parallelogram.
Question 10.
ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see Fig. 8.21). Show that
(i) ΔAPB ≅ ΔCQD
(ii) AP = CQ
Solution:
(i) In ΔAPB and ΔCQD,
∠ABP = ∠CDQ (Alternate interior angles)
∠APB = ∠CQD (= 90o as AP and CQ are perpendiculars)
AB = CD (ABCD is a parallelogram)
, ΔAPB ≅ ΔCQD [AAS congruency]
(ii) As ΔAPB ≅ ΔCQD.
, AP = CQ [CPCT]
Question 11.
In ΔABC and ΔDEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F respectively (see Fig. 8.22).
Show that
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ΔABC ≅ ΔDEF.
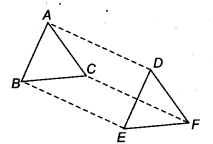
Solution:
(i) We have AB = DE [Given]
and AB || DE [Given]
i. e., ABED is a quadrilateral in which a pair of opposite sides (AB and DE) are parallel and of equal length.
∴ ABED is a parallelogram.
(ii) BC = EF [Given]
and BC || EF [Given]
i.e. BEFC is a quadrilateral in which a pair of opposite sides (BC and EF) are parallel and of equal length.
∴ BEFC is a parallelogram.
(iii) ABED is a parallelogram [Proved]
∴ AD || BE and AD = BE …(1)
[ ∵ Opposite sides of a parallelogram are equal and parallel] Also, BEFC is a parallelogram. [Proved]
BE || CF and BE = CF …(2)
[ ∵ Opposite sides of a parallelogram are equal and parallel]
From (1) and (2), we have
AD || CF and AD = CF
(iv) Since, AD || CF and AD = CF [Proved]
i.e., In quadrilateral ACFD, one pair of opposite sides (AD and CF) are parallel and of equal length.
∴Quadrilateral ACFD is a parallelogram.
(v) Since, ACFD is a parallelogram. [Proved]
So, AC =DF [∵ Opposite sides of a parallelogram are equal]
(vi) In ∆ABC and ∆DFF, we have
AB = DE [Given]
BC = EF [Given]
AC = DE [Proved in (v) part]
∆ABC ≅ ∆DFF [By SSS congruency]
Question 12.
ABCD is a trapezium in which AB || CD and AD = BC (see figure). Show that
(i )∠A=∠B
(ii )∠C=∠D
(iii) ∆ABC ≅ ∆BAD
(iv) diagonal AC = diagonal BD
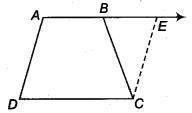
Solution:
To Construct: Draw a line through C parallel to DA intersecting AB produced at E.
(i) CE = AD (Opposite sides of a parallelogram)
AD = BC (Given)
, BC = CE
⇒∠CBE = ∠CEB
also,
∠A+∠CBE = 180° (Angles on the same side of transversal and ∠CBE = ∠CEB)
∠B +∠CBE = 180° ( As Linear pair)
⇒∠A = ∠B
(ii) ∠A+∠D = ∠B+∠C = 180° (Angles on the same side of transversal)
⇒∠A+∠D = ∠A+∠C (∠A = ∠B)
⇒∠D = ∠C
(iii) In ΔABC and ΔBAD,
AB = AB (Common)
∠DBA = ∠CBA
AD = BC (Given)
, ΔABC ≅ ΔBAD [SAS congruency]
(iv) Diagonal AC = diagonal BD by CPCT as ΔABC ≅ ΔBA.
Question 1.
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see figure). AC is a diagonal. Show that
(i) SR || AC and SR = 
(ii) PQ = SR
(iii) PQRS is a parallelogram.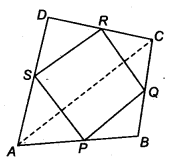
Solution:
(i) In ∆ACD, We have
∴ S is the mid-point of AD and R is the mid-point of CD.
SR =
[By mid-point theorem]
(ii) In ∆ABC, P is the mid-point of AB and Q is the mid-point of BC.
PQ =
[By mid-point theorem]
From (1) and (2), we get
PQ =
⇒ PQ = SR and PQ || SR
(iii) In a quadrilateral PQRS,
PQ = SR and PQ || SR [Proved]
∴ PQRS is a parallelogram.
Question 2.
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rectangle.
Solution:
We have a rhombus ABCD and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Join AC.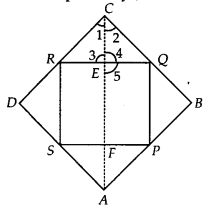
In ∆ABC, P and Q are the mid-points of AB and BC respectively.
∴ PQ =
[By mid-point theorem]
In ∆ADC, R and S are the mid-points of CD and DA respectively.
∴ SR =
[By mid-point theorem]
From (1) and (2), we get
PQ =
⇒ PQ = SR and PQ || SR
∴ PQRS is a parallelogram. …….(3)
Now, in ∆ERC and ∆EQC,
∠1 = ∠2
[ ∵ The diagonals of a rhombus bisect the opposite angles]
CR = CQ [ ∵
CE = CE [Common]
∴ ∆ERC ≅ ∆EQC [By SAS congruency]
⇒ ∠3 = ∠4 …(4) [By C.P.C.T.]
But ∠3 + ∠4 = 180° ……(5) [Linear pair]
From (4) and (5), we get
⇒ ∠3 = ∠4 = 90°
Now, ∠RQP = 180° – ∠b [ Y Co-interior angles for PQ || AC and EQ is transversal]
But ∠5 = ∠3
[ ∵ Vertically opposite angles are equal]
∴ ∠5 = 90°
So, ∠RQP = 180° – ∠5 = 90°
∴ One angle of parallelogram PQRS is 90°.
Thus, PQRS is a rectangle.
Question 3.
ABCD is a rectangle and P, Q, R ans S are mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rhombus.
Solution:
We have,
Now, in ∆ABC, we have
PQ =
[By mid-point theorem]
Similarly, in ∆ADC, we have
SR =
From (1) and (2), we get
PQ = SR and PQ || SR
∴ PQRS is a parallelogram.
Now, in ∆PAS and ∆PBQ, we have
∠A = ∠B [Each 90°]
AP = BP [ ∵ P is the mid-point of AB]
AS = BQ [∵
∴ ∆PAS ≅ ∆PBQ [By SAS congruency]
⇒ PS = PQ [By C.P.C.T.]
Also, PS = QR and PQ = SR [∵opposite sides of a parallelogram are equal]
So, PQ = QR = RS = SP i.e., PQRS is a parallelogram having all of its sides equal.
Hence, PQRS is a rhombus.
Question 4.
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see figure). Show that F is the mid-point of BC.
Solution:
We have,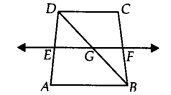
In ∆DAB, we know that E is the mid-point of
AD and EG || AB [∵ EF || AB]
Using the converse of mid-point theorem, we get, G is the mid-point of BD.
Again in ABDC, we have G is the midpoint of BD and GF || DC.
[∵ AB || DC and EF || AB and GF is a part of EF]
Using the converse of the mid-point theorem, we get, F is the mid-point of BC.
Question 5.
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see figure). Show that the line segments AF and EC trisect the diagonal BD.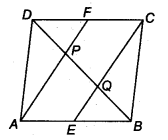
Solution:
Since, the opposite sides of a parallelogram are parallel and equal.
∴ AB || DC
⇒ AE || FC …(1)
and AB = DC
⇒
⇒ AE = FC …(2)
From (1) and (2), we have
AE || PC and AE = PC
∴ ∆ECF is a parallelogram.
Now, in ∆DQC, we have F is the mid-point of DC and FP || CQ
[∵ AF || CE]
⇒ DP = PQ …(3)
[By converse of mid-point theorem] Similarly, in A BAP, E is the mid-point of AB and EQ || AP [∵AF || CE]
⇒ BQ = PQ …(4)
[By converse of mid-point theorem]
∴ From (3) and (4), we have
DP = PQ = BQ
So, the line segments AF and EC trisect the diagonal BD.
Question 6.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Solution:
Let ABCD be a quadrilateral, where P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively.
Join PQ, QR, RS and SP.
Let us also join PR, SQ and AC.
Now, in ∆ABC, we have P and Q are the mid-points of its sides AB and BC respectively.
∴ PQ || AC and PQ =
[By mid-point theorem]
Similarly, RS || AC and RS =
∴ By (1) and (2), we get
PQ || RS, PQ = RS
∴ PQRS is a parallelogram.
And the diagonals of a parallelogram bisect each other, i.e., PR and SQ bisect each other. Thus, the line segments joining the midpoints of opposite sides of a quadrilateral ABCD bisect each other.
Question 7.
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA =
Solution:
we have
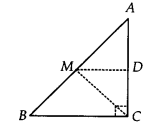
(i) In ∆ACB, We have
M is the mid-point of AB. [Given]
MD || BC , [Given]
∴ Using the converse of mid-point theorem,
D is the mid-point of AC.
(ii) Since, MD || BC and AC is a transversal.
∠MDA = ∠BCA
[ ∵ Corresponding angles are equal] As
∠BCA = 90° [Given]
∠MDA = 90°
⇒ MD ⊥AC.
(iii) In ∆ADM and ∆CDM, we have
∠ADM = ∠CDM [Each equal to 90°]
MD = MD [Common]
AD = CD [∵ D is the mid-point of AC]
∴ ∆ADM ≅ ∆CDM [By SAS congruency]
⇒ MA = MC [By C.P.C.T.] .. .(1)
∵ M is the mid-point of AB [Given]
MA =
From (1) and (2), we have
CM = MA =