Chapter 12 of the NCERT Maths textbook for Class 7 focuses on algebraic expressions. It introduces concepts such as variables, constants, coefficients, and the formation of algebraic expressions. Students learn to simplify expressions by combining like terms and performing basic operations like addition and subtraction.
NCERT Solutions for Class 7 Maths Chapter 12 Algebraic expressions EX- 12.1 and 12.2
We try to teach you all Questions in easy way. We solve all chapter wise sums of maths textbook. In every chapter include NCERT solutions. For solutions of Exercise 12.1, 12.2, 12.3, 12.4
NCERT Solutions of class 7th maths Chapter 12 Algebraic expressions Ex- 12.1
1. Get the algebraic expressions in the following cases using variables, constants and arithmetic operations.
(i) Subtraction of z from y.
Solution:-
= Y – z
(ii) One-half of the sum of numbers x and y.
Solution:-
= ½ (x + y)
= (x + y)/2
(iii) The number z multiplied by itself.
Solution:-
= z × z
= z2
(iv) One-fourth of the product of numbers p and q.
Solution:-
= ¼ (p × q)
= pq/4
(v) Numbers x and y both squared and added.
Solution:-
= x2 + y2
(vi) Number 5 added to three times the product of numbers m and n.
Solution:-
= 3mn + 5
(vii) Product of numbers y and z subtracted from 10.
Solution:-
= 10 – (y × z)
= 10 – yz
(viii) Sum of numbers a and b subtracted from their product.
Solution:-
= (a × b) – (a + b)
= ab – (a + b)
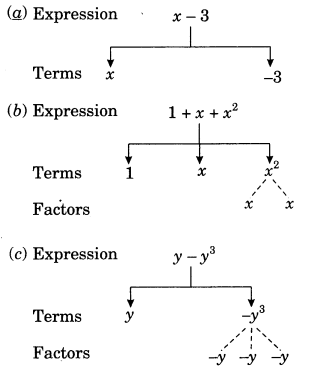
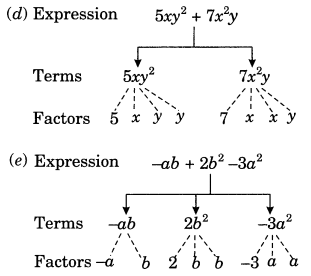
2. (i) Identify the terms and their factors in the following expressions
Show the terms and factors by tree diagrams.
(a) x – 3
(b) 1 + x + x2
(c) y – y3
(d) 5xy2 + 7x2 y
(e) -ab + 2b2 – 3a2
Solution:
(ii) Identify terms and factors in the expression
given below:
(a) -4x + 5
(b) -4x + 5y
(c) 5y + 3y2
(d) xy + 2x2y2
(e) pq + q
(f) 1.2ab – 2.4b + 3.6a
(g) 34x+14
(h) 0.1p2 + 0.2q2
Solution:

Question 4.
(a) Identify terms which contain x and give the
coefficient of x.
(i) y2x + y
(ii) 13y2 – 8yx
(iii) x + y + 2
(iv) 5 + z + zx
(v) 1 + x + xy
(vi) 12 xy2 + 25
(vii) 7x + xy2
Solution:

(b) Identify terms which contain y2 and give the coefficients of y2.
(i) 8 – xy2
(ii) 5y2 + 7x
(iii) 2x2y – 15xy2 + 7y2
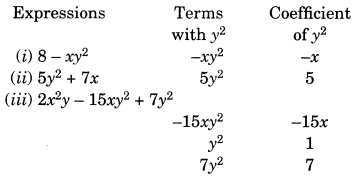
Question 5.
Classify into monomials, binomials and trinomials:
(i) 4y – 7x
(ii) y2
(iii) x + y – xy
(iv) 100
(v) ab – a – b
(vi) 5 – 3t
(vii) 4p2q – 4pq2
(viii) 7mn
(ix) z2 – 3z + 8
(x) a2 + b2
(xi) z2 + z
(xii) 1 + x + x2
Solution:
(i)4y – 7z – Binomial
(ii) y2 – Monomial
(iii) x + y – xy – Trinomial
(iv) 100 Monomial
(v) ab – a – b – Trinomial
(vi) 5 – 3t – Binomial
(vii) 4p2q – 4pq2 – Binomial
(viii) 7mn – Monomial
(ix) z2 -3z + 8 – Trinomial
(x) a2 + b2 – Binomial
(xi) z2 + z – Binomial
(xii) 1 + x + x2 – Trinomial
Question 6.
State whether a given pair of terms is of like or unlike terms.
(i) 1, 100
(ii) -7x, 52x
(iii) -29x, -29y
(iv) 14xy, 42yx
(v) 4m2p, 4mp2
(vi) 12xz, 12 x2y2
Solution:
(i) 1, 100 – Like
(ii) -7x, 52x – Like
(iii) -29x, -29y – Unlike
(iv) 14xy, 42yx – Like
(v) 4m2p, 4mp2 – Unlike
(vi) 12xz, 12x2z2 – Unlike
Question 7.
Identify like terms in the following:
(a)-xy2, -4yx2, 8×2, 2xy2, 7y2, -11×2, -100x, -11yx, 20x2y, -6×2, y, 2xy, 3x
(b) 10pq, 7p, 8q, -p2q2, -7qp, -100q, -23, 12q2p2, -5p2, 41, 2405p, 78qp, 13p2q, qp2, 701p2
Solution:
(a) Like terms are:
(i) -xy2, 2xy2
(ii) -4yx2, 20x2y
(iii)8×2, -11×2, -6×2
(iv) 7y, y
(v) -100x, 3x
(vi) -11yx, 2xy
(b) Like terms are:
(i) 10pq, – 7qp, 78qp
(ii) 7p, 2405p
(iii) 8q, -100q
(iv) -p2q2, 12 q2p2
(v) -23, 41
(vi) -5p2, 701p2
NCERT Solutions of class 7th maths Chapter 12 Algebraic expressions Ex- 12.2
1. Simplify combining like terms:
(i) 21b – 32 + 7b – 20b
Solution:-
When term have the same algebraic factors, they are like terms.
Then,
= (21b + 7b – 20b) – 32
= b (21 + 7 – 20) – 32
= b (28 – 20) – 32
= b (8) – 32
= 8b – 32
(ii) – z2 + 13z2 – 5z + 7z3 – 15z
Solution:-
When term have the same algebraic factors, they are like terms.
Then,
= 7z3 + (-z2 + 13z2) + (-5z – 15z)
= 7z3 + z2 (-1 + 13) + z (-5 – 15)
= 7z3 + z2 (12) + z (-20)
= 7z3 + 12z2 – 20z
(iii) p – (p – q) – q – (q – p)
Solution:-
When term have the same algebraic factors, they are like terms.
Then,
= p – p + q – q – q + p
= p – q
(iv) 3a – 2b – ab – (a – b + ab) + 3ab + b – a
Solution:-
When term have the same algebraic factors, they are like terms.
Then,
= 3a – 2b – ab – a + b – ab + 3ab + b – a
= 3a – a – a – 2b + b + b – ab – ab + 3ab
= a (1 – 1- 1) + b (-2 + 1 + 1) + ab (-1 -1 + 3)
= a (1 – 2) + b (-2 + 2) + ab (-2 + 3)
= a (1) + b (0) + ab (1)
= a + ab
(v) 5x2y – 5×2 + 3yx2 – 3y2 + x2 – y2 + 8xy2 – 3y2
Solution:-
When term have the same algebraic factors, they are like terms.
Then,
= 5x2y + 3yx2 – 5×2 + x2 – 3y2 – y2 – 3y2
= x2y (5 + 3) + x2 (- 5 + 1) + y2 (-3 – 1 -3) + 8xy2
= x2y (8) + x2 (-4) + y2 (-7) + 8xy2
= 8x2y – 4×2 – 7y2 + 8xy2
(vi) (3y2 + 5y – 4) – (8y – y2 – 4)
Solution:-
When term have the same algebraic factors, they are like terms.
Then,
= 3y2 + 5y – 4 – 8y + y2 + 4
= 3y2 + y2 + 5y – 8y – 4 + 4
= y2 (3 + 1) + y (5 – 8) + (-4 + 4)
= y2 (4) + y (-3) + (0)
= 4y2 – 3y
2. Add:
(i) 3mn, – 5mn, 8mn, – 4mn
Solution:-
When term have the same algebraic factors, they are like terms.
Then, we have to add the like terms
= 3mn + (-5mn) + 8mn + (- 4mn)
= 3mn – 5mn + 8mn – 4mn
= mn (3 – 5 + 8 – 4)
= mn (11 – 9)
= mn (2)
= 2mn
(ii) t – 8tz, 3tz – z, z – t
Solution:-
When term have the same algebraic factors, they are like terms.
Then, we have to add the like terms
= t – 8tz + (3tz – z) + (z – t)
= t – 8tz + 3tz – z + z – t
= t – t – 8tz + 3tz – z + z
= t (1 – 1) + tz (- 8 + 3) + z (-1 + 1)
= t (0) + tz (- 5) + z (0)
= – 5tz
(iii) – 7mn + 5, 12mn + 2, 9mn – 8, – 2mn – 3
Solution:-
When term have the same algebraic factors, they are like terms.
Then, we have to add the like terms
= – 7mn + 5 + 12mn + 2 + (9mn – 8) + (- 2mn – 3)
= – 7mn + 5 + 12mn + 2 + 9mn – 8 – 2mn – 3
= – 7mn + 12mn + 9mn – 2mn + 5 + 2 – 8 – 3
= mn (-7 + 12 + 9 – 2) + (5 + 2 – 8 – 3)
= mn (- 9 + 21) + (7 – 11)
= mn (12) – 4
= 12mn – 4
(iv) a + b – 3, b – a + 3, a – b + 3
Solution:-
When term have the same algebraic factors, they are like terms.
Then, we have to add the like terms
= a + b – 3 + (b – a + 3) + (a – b + 3)
= a + b – 3 + b – a + 3 + a – b + 3
= a – a + a + b + b – b – 3 + 3 + 3
= a (1 – 1 + 1) + b (1 + 1 – 1) + (-3 + 3 + 3)
= a (2 -1) + b (2 -1) + (-3 + 6)
= a (1) + b (1) + (3)
= a + b + 3
(v) 14x + 10y – 12xy – 13, 18 – 7x – 10y + 8xy, 4xy
Solution:-
When term have the same algebraic factors, they are like terms.
Then, we have to add the like terms
= 14x + 10y – 12xy – 13 + (18 – 7x – 10y + 8xy) + 4xy
= 14x + 10y – 12xy – 13 + 18 – 7x – 10y + 8xy + 4xy
= 14x – 7x + 10y– 10y – 12xy + 8xy + 4xy – 13 + 18
= x (14 – 7) + y (10 – 10) + xy(-12 + 8 + 4) + (-13 + 18)
= x (7) + y (0) + xy(0) + (5)
= 7x + 5
(vi) 5m – 7n, 3n – 4m + 2, 2m – 3mn – 5
Solution:-
When term have the same algebraic factors, they are like terms.
Then, we have to add the like terms
= 5m – 7n + (3n – 4m + 2) + (2m – 3mn – 5)
= 5m – 7n + 3n – 4m + 2 + 2m – 3mn – 5
= 5m – 4m + 2m – 7n + 3n – 3mn + 2 – 5
= m (5 – 4 + 2) + n (-7 + 3) – 3mn + (2 – 5)
= m (3) + n (-4) – 3mn + (-3)
= 3m – 4n – 3mn – 3
(vii) 4x2y, – 3xy2, –5xy2, 5x2y
Solution:-
When term have the same algebraic factors, they are like terms.
Then, we have to add the like terms
= 4x2y + (-3xy2) + (-5xy2) + 5x2y
= 4x2y + 5x2y – 3xy2 – 5xy2
= x2y (4 + 5) + xy2 (-3 – 5)
= x2y (9) + xy2 (- 8)
= 9x2y – 8xy2
(viii) 3p2q2 – 4pq + 5, – 10 p2q2, 15 + 9pq + 7p2q2
Solution:-
When term have the same algebraic factors, they are like terms.
Then, we have to add the like terms
= 3p2q2 – 4pq + 5 + (- 10p2q2) + 15 + 9pq + 7p2q2
= 3p2q2 – 10p2q2 + 7p2q2 – 4pq + 9pq + 5 + 15
= p2q2 (3 -10 + 7) + pq (-4 + 9) + (5 + 15)
= p2q2 (0) + pq (5) + 20
= 5pq + 20
(ix) ab – 4a, 4b – ab, 4a – 4b
Solution:-
When term have the same algebraic factors, they are like terms.
Then, we have to add the like terms
= ab – 4a + (4b – ab) + (4a – 4b)
= ab – 4a + 4b – ab + 4a – 4b
= ab – ab – 4a + 4a + 4b – 4b
= ab (1 -1) + a (4 – 4) + b (4 – 4)
= ab (0) + a (0) + b (0)
= 0
(x) x2 – y2 – 1, y2 – 1 – x2, 1 – x2 – y2
Solution:-
When term have the same algebraic factors, they are like terms.
Then, we have to add the like terms
= x2 – y2 – 1 + (y2 – 1 – x2) + (1 – x2 – y2)
= x2 – y2 – 1 + y2 – 1 – x2 + 1 – x2 – y2
= x2 – x2 – x2 – y2 + y2 – y2 – 1 – 1 + 1
= x2 (1 – 1- 1) + y2 (-1 + 1 – 1) + (-1 -1 + 1)
= x2 (1 – 2) + y2 (-2 +1) + (-2 + 1)
= x2 (-1) + y2 (-1) + (-1)
= -x2 – y2 -1
3. Subtract:
(i) –5y2 from y2
Solution:-
When term have the same algebraic factors, they are like terms.
Then, we have to subtract the like terms
= y2 – (-5y2)
= y2 + 5y2
= 6y2
(ii) 6xy from –12xy
Solution:-
When term have the same algebraic factors, they are like terms.
Then, we have to subtract the like terms
= -12xy – 6xy
= – 18xy
(iii) (a – b) from (a + b)
Solution:-
When term have the same algebraic factors, they are like terms.
Then, we have to subtract the like terms
= (a + b) – (a – b)
= a + b – a + b
= a – a + b + b
= a (1 – 1) + b (1 + 1)
= a (0) + b (2)
= 2b
(iv) a (b – 5) from b (5 – a)
Solution:-
When term have the same algebraic factors, they are like terms.
Then, we have to subtract the like terms
= b (5 -a) – a (b – 5)
= 5b – ab – ab + 5a
= 5b + ab (-1 -1) + 5a
= 5a + 5b – 2ab
(v) –m2 + 5mn from 4m2 – 3mn + 8
Solution:-
When term have the same algebraic factors, they are like terms.
Then, we have to subtract the like terms
= 4m2 – 3mn + 8 – (- m2 + 5mn)
= 4m2 – 3mn + 8 + m2 – 5mn
= 4m2 + m2 – 3mn – 5mn + 8
= 5m2 – 8mn + 8
(vi) – x2 + 10x – 5 from 5x – 10
Solution:-
When term have the same algebraic factors, they are like terms.
Then, we have to subtract the like terms
= 5x – 10 – (-x2 + 10x – 5)
= 5x – 10 + x2 – 10x + 5
= x2 + 5x – 10x – 10 + 5
= x2 – 5x – 5
(vii) 5a2 – 7ab + 5b2 from 3ab – 2a2 – 2b2
Solution:-
When term have the same algebraic factors, they are like terms.
Then, we have to subtract the like terms
= 3ab – 2a2 – 2b2 – (5a2 – 7ab + 5b2)
= 3ab – 2a2 – 2b2 – 5a2 + 7ab – 5b2
= 3ab + 7ab – 2a2 – 5a2 – 2b2 – 5b2
= 10ab – 7a2 – 7b2
(viii) 4pq – 5q2 – 3p2 from 5p2 + 3q2 – pq
Solution:-
When term have the same algebraic factors, they are like terms.
Then, we have to subtract the like terms
= 5p2 + 3q2 – pq – (4pq – 5q2 – 3p2)
= 5p2 + 3q2 – pq – 4pq + 5q2 + 3p2
= 5p2 + 3p2 + 3q2 + 5q2 – pq – 4pq
= 8p2 + 8q2 – 5pq
4. (a) What should be added to x2 + xy + y2 to obtain 2×2 + 3xy?
Solution:-
Let us assume p be the required term
Then,
p + (x2 + xy + y2) = 2×2 + 3xy
p = (2×2 + 3xy) – (x2 + xy + y2)
p = 2×2 + 3xy – x2 – xy – y2
p = 2×2 – x2 + 3xy – xy – y2
p = x2 + 2xy – y2
(b) What should be subtracted from 2a + 8b + 10 to get – 3a + 7b + 16?
Solution:-
Let us assume x be the required term
Then,
2a + 8b + 10 – x = -3a + 7b + 16
x = (2a + 8b + 10) – (-3a + 7b + 16)
x = 2a + 8b + 10 + 3a – 7b – 16
x = 2a + 3a + 8b – 7b + 10 – 16
x = 5a + b – 6
5. What should be taken away from 3×2 – 4y2 + 5xy + 20 to obtain – x2 – y2 + 6xy + 20?
Solution:-
Let us assume a be the required term
Then,
3×2 – 4y2 + 5xy + 20 – a = -x2 – y2 + 6xy + 20
a = 3×2 – 4y2 + 5xy + 20 – (-x2 – y2 + 6xy + 20)
a = 3×2 – 4y2 + 5xy + 20 + x2 + y2 – 6xy – 20
a = 3×2 + x2 – 4y2 + y2 + 5xy – 6xy + 20 – 20
a = 4×2 – 3y2 – xy
6. (a) From the sum of 3x – y + 11 and – y – 11, subtract 3x – y – 11.
Solution:-
First we have to find out the sum of 3x – y + 11 and – y – 11
= 3x – y + 11 + (-y – 11)
= 3x – y + 11 – y – 11
= 3x – y – y + 11 – 11
= 3x – 2y
Now, subtract 3x – y – 11 from 3x – 2y
= 3x – 2y – (3x – y – 11)
= 3x – 2y – 3x + y + 11
= 3x – 3x – 2y + y + 11
= -y + 11
(b) From the sum of 4 + 3x and 5 – 4x + 2×2, subtract the sum of 3×2 – 5x and
–x2 + 2x + 5.
Solution:-
First we have to find out the sum of 4 + 3x and 5 – 4x + 2×2
= 4 + 3x + (5 – 4x + 2×2)
= 4 + 3x + 5 – 4x + 2×2
= 4 + 5 + 3x – 4x + 2×2
= 9 – x + 2×2
= 2×2 – x + 9 … [equation 1]
Then, we have to find out the sum of 3×2 – 5x and – x2 + 2x + 5
= 3×2 – 5x + (-x2 + 2x + 5)
= 3×2 – 5x – x2 + 2x + 5
= 3×2 – x2 – 5x + 2x + 5
= 2×2 – 3x + 5 … [equation 2]
Now, we have to subtract equation (2) from equation (1)
= 2×2 – x + 9 – (2×2 – 3x + 5)
= 2×2 – x + 9 – 2×2 + 3x – 5
= 2×2 – 2×2 – x + 3x + 9 – 5
= 2x + 4
NCERT Solutions of class 7th maths Chapter 12 Algebraic expressions Ex- 12.3
1. If m = 2, find the value of:
(i) m – 2
Solution:-
From the question it is given that m = 2
Then, substitute the value of m in the question
= 2 -2
= 0
(ii) 3m – 5
Solution:-
From the question it is given that m = 2
Then, substitute the value of m in the question
= (3 × 2) – 5
= 6 – 5
= 1
(iii) 9 – 5m
Solution:-
From the question it is given that m = 2
Then, substitute the value of m in the question
= 9 – (5 × 2)
= 9 – 10
= – 1
(iv) 3m2 – 2m – 7
Solution:-
From the question it is given that m = 2
Then, substitute the value of m in the question
= (3 × 22) – (2 × 2) – 7
= (3 × 4) – (4) – 7
= 12 – 4 -7
= 12 – 11
= 1
(v) (5m/2) – 4
Solution:-
From the question it is given that m = 2
Then, substitute the value of m in the question
= ((5 × 2)/2) – 4
= (10/2) – 4
= 5 – 4
= 1
2. If p = – 2, find the value of:
(i) 4p + 7
Solution:-
From the question it is given that p = -2
Then, substitute the value of p in the question
= (4 × (-2)) + 7
= -8 + 7
= -1
(ii) – 3p2 + 4p + 7
Solution:-
From the question it is given that p = -2
Then, substitute the value of p in the question
= (-3 × (-2)2) + (4 × (-2)) + 7
= (-3 × 4) + (-8) + 7
= -12 – 8 + 7
= -20 + 7
= -13
(iii) – 2p3 – 3p2 + 4p + 7
Solution:-
From the question it is given that p = -2
Then, substitute the value of p in the question
= (-2 × (-2)3) – (3 × (-2)2) + (4 × (-2)) + 7
= (-2 × -8) – (3 × 4) + (-8) + 7
= 16 – 12 – 8 + 7
= 23 – 20
= 3
3. Find the value of the following expressions, when x = –1:
(i) 2x – 7
Solution:-
From the question it is given that x = -1
Then, substitute the value of x in the question
= (2 × -1) – 7
= – 2 – 7
= – 9
(ii) – x + 2
Solution:-
From the question it is given that x = -1
Then, substitute the value of x in the question
= – (-1) + 2
= 1 + 2
= 3
(iii) x2 + 2x + 1
Solution:-
From the question it is given that x = -1
Then, substitute the value of x in the question
= (-1)2 + (2 × -1) + 1
= 1 – 2 + 1
= 2 – 2
= 0
(iv) 2x2 – x – 2
Solution:-
From the question it is given that x = -1
Then, substitute the value of x in the question
= (2 × (-1)2) – (-1) – 2
= (2 × 1) + 1 – 2
= 2 + 1 – 2
= 3 – 2
= 1
4. If a = 2, b = – 2, find the value of:
(i) a2 + b2
Solution:-
From the question it is given that a = 2, b = -2
Then, substitute the value of a and b in the question
= (2)2 + (-2)2
= 4 + 4
= 8
(ii) a2 + ab + b2
Solution:-
From the question it is given that a = 2, b = -2
Then, substitute the value of a and b in the question
= 22 + (2 × -2) + (-2)2
= 4 + (-4) + (4)
= 4 – 4 + 4
= 4
(iii) a2 – b2
Solution:-
From the question it is given that a = 2, b = -2
Then, substitute the value of a and b in the question
= 22 – (-2)2
= 4 – (4)
= 4 – 4
= 0
5. When a = 0, b = – 1, find the value of the given expressions:
(i) 2a + 2b
Solution:-
From the question it is given that a = 0, b = -1
Then, substitute the value of a and b in the question
= (2 × 0) + (2 × -1)
= 0 – 2
= -2
(ii) 2a2 + b2 + 1
Solution:-
From the question it is given that a = 0, b = -1
Then, substitute the value of a and b in the question
= (2 × 02) + (-1)2 + 1
= 0 + 1 + 1
= 2
(iii) 2a2b + 2ab2 + ab
Solution:-
From the question it is given that a = 0, b = -1
Then, substitute the value of a and b in the question
= (2 × 02 × -1) + (2 × 0 × (-1)2) + (0 × -1)
= 0 + 0 +0
= 0
(iv) a2 + ab + 2
Solution:-
From the question it is given that a = 0, b = -1
Then, substitute the value of a and b in the question
= (02) + (0 × (-1)) + 2
= 0 + 0 + 2
= 2
6. Simplify the expressions and find the value if x is equal to 2
(i) x + 7 + 4 (x – 5)
Solution:-
From the question it is given that x = 2
We have,
= x + 7 + 4x – 20
= 5x + 7 – 20
Then, substitute the value of x in the equation
= (5 × 2) + 7 – 20
= 10 + 7 – 20
= 17 – 20
= – 3
(ii) 3 (x + 2) + 5x – 7
Solution:-
From the question it is given that x = 2
We have,
= 3x + 6 + 5x – 7
= 8x – 1
Then, substitute the value of x in the equation
= (8 × 2) – 1
= 16 – 1
= 15
(iii) 6x + 5 (x – 2)
Solution:-
From the question it is given that x = 2
We have,
= 6x + 5x – 10
= 11x – 10
Then, substitute the value of x in the equation
= (11 × 2) – 10
= 22 – 10
= 12
(iv) 4(2x – 1) + 3x + 11
Solution:-
From the question it is given that x = 2
We have,
= 8x – 4 + 3x + 11
= 11x + 7
Then, substitute the value of x in the equation
= (11 × 2) + 7
= 22 + 7
= 29
7. Simplify these expressions and find their values if x = 3, a = – 1, b = – 2.
(i) 3x – 5 – x + 9
Solution:-
From the question it is given that x = 3
We have,
= 3x – x – 5 + 9
= 2x + 4
Then, substitute the value of x in the equation
= (2 × 3) + 4
= 6 + 4
= 10
(ii) 2 – 8x + 4x + 4
Solution:-
From the question it is given that x = 3
We have,
= 2 + 4 – 8x + 4x
= 6 – 4x
Then, substitute the value of x in the equation
= 6 – (4 × 3)
= 6 – 12
= – 6
(iii) 3a + 5 – 8a + 1
Solution:-
From the question it is given that a = -1
We have,
= 3a – 8a + 5 + 1
= – 5a + 6
Then, substitute the value of a in the equation
= – (5 × (-1)) + 6
= – (-5) + 6
= 5 + 6
= 11
(iv) 10 – 3b – 4 – 5b
Solution:-
From the question it is given that b = -2
We have,
= 10 – 4 – 3b – 5b
= 6 – 8b
Then, substitute the value of b in the equation
= 6 – (8 × (-2))
= 6 – (-16)
= 6 + 16
= 22
(v) 2a – 2b – 4 – 5 + a
Solution:-
From the question it is given that a = -1, b = -2
We have,
= 2a + a – 2b – 4 – 5
= 3a – 2b – 9
Then, substitute the value of a and b in the equation
= (3 × (-1)) – (2 × (-2)) – 9
= -3 – (-4) – 9
= – 3 + 4 – 9
= -12 + 4
= -8
8. (i) If z = 10, find the value of z3 – 3(z – 10).
Solution:-
From the question it is given that z = 10
We have,
= z3 – 3z + 30
Then, substitute the value of z in the equation
= (10)3 – (3 × 10) + 30
= 1000 – 30 + 30
= 1000
(ii) If p = – 10, find the value of p2 – 2p – 100
Solution:-
From the question it is given that p = -10
We have,
= p2 – 2p – 100
Then, substitute the value of p in the equation
= (-10)2 – (2 × (-10)) – 100
= 100 + 20 – 100
= 20
9. What should be the value of a if the value of 2x2 + x – a equals to 5, when x = 0?
Solution:-
From the question it is given that x = 0
We have,
2x2 + x – a = 5
a = 2x2 + x – 5
Then, substitute the value of x in the equation
a = (2 × 02) + 0 – 5
a = 0 + 0 – 5
a = -5
10. Simplify the expression and find its value when a = 5 and b = – 3.
2(a2 + ab) + 3 – ab
Solution:-
From the question it is given that a = 5 and b = -3
We have,
= 2a2 + 2ab + 3 – ab
= 2a2 + ab + 3
Then, substitute the value of a and b in the equation
= (2 × 52) + (5 × (-3)) + 3
= (2 × 25) + (-15) + 3
= 50 – 15 + 3
= 53 – 15
= 38
NCERT Solutions of class 7th maths Chapter 12 Algebraic expressions Ex- 12.4
Question 1.
Observe the patterns of digits made from line segments of equal length. You will find such segmented digits on the display of electronic watches or calculators.

If the number of digits formed is taken to be n, the number of segments required to form n digits is given by the algebraic expression appearing on the right of each pattern. How many segments are required to form 5, 10, 100 digits of the kind 6, 4, 3.
Solution:
(i) The number of line segments required to form
n digits is given by the expressions.
6 = 5n + 1
For 5 figures, the number of line segments = 5 × 5 + 1 = 25 + 1 = 26
For 10 figures, the number of line segments = 5 × 10 + 1
= 50 + 1 = 51
For 100 figures, the number of line segments = 5 × 100 + 1
= 500 + 1 = 501
4 = 3n + 1
For 5 figures, the number of line segments =3 ×5 + 1
= 15 + 1 = 16
For 10 figures, the number of line segments = 3 × 10 + 1
= 30 + 1 = 31
For 100 figures, the number of line segments = 3 × 100 + 1
= 300 + 1 = 301
8 = 5n + 1
For 5 figures, the number of line numbers = 5 × 5 + 2
= 25 + 2 = 27
For 10 figures, the number of line segments = 5 × 10 + 2
= 50 + 2 = 52
For 100 figures, the number of line segments = 5 × 100 + 2
= 500 + 2 = 502
Question 2.
Use the given algebraic expression to complete the table of number patterns:
| S.No. | Expression | Terms | |||||||||
| 1st | 2nd | 3rd | 4th | 5th | … | 10th | … | 100th | … | ||
| (i) | 2n – 1 | 1 | 3 | 5 | 7 | 9 | – | 19 | – | – | – |
| (ii) | 3n + 2 | 5 | 8 | 11 | 14 | – | – | – | – | – | – |
| (iii) | 4n + 1 | 5 | 9 | 13 | 17 | – | – | – | – | – | – |
| (iv) | 7n + 20 | 27 | 34 | 41 | 48 | – | – | – | – | – | – |
| (v) | n2 + 1 | 2 | 5 | 10 | 17 | – | – | – | – | 10,001 | – |
Solution:
(i) Given expression is 2n – 1
For n = 100, 2 × 100 – 1
= 200 – 1 = 199
(ii) Given expression is 3n + 2
For n = 5, 3 × 5 + 2 = 15 + 2 = 17
For n = 10, 3 × 10 + 2 = 30 + 2 = 32
For n = 100, 3 × 100 + 2 = 300 + 2 = 302
(iii) Given expression is 4n + 1
For n = 5, 4 × 5 + 1 = 20 + 1 = 21
For n = 10, 4 × 10 + 1 = 40 + 1 = 41
For n = 100, 4 × 100 + 1 = 400 + 1 = 401
(iv) Given expression is 7n + 20
For n = 5, 7 × 5 + 20 = 35 + 20 = 55
For n = 10, 7 × 10 + 20 = 70 + 20 = 90
For n = 100, 7 × 100 + 20 = 700 + 20 = 720
(v) Given expression is n2 + 1
For n = 5, 52 + 1 = 25 + 1 = 26
For n = 10, 102 + 1 = 100 + 1 = 101
