NCERT Solutions Maths Chapter 3 Trigonometric Functions For Class 11

Chapter 3 of NCERT Maths for Class 11, titled “Trigonometric Functions,” introduces the fundamental concepts of trigonometry and explores the relationships between the angles and sides of a triangle. It covers the six trigonometric ratios—sine, cosine, tangent, cosecant, secant, and cotangent—defining them in terms of a right-angled triangle. The chapter also delves into the unit circle, allowing students to understand the trigonometric functions for all real angles, not just those in a right triangle. Additionally, the chapter explores the graphical representation of these functions, their properties, and how to evaluate them for different angles. Students are also introduced to the concepts of amplitude, period, and phase shift. The chapter lays the foundation for more advanced trigonometric identities and equations, helping students develop a deeper understanding of the subject.

NCERT Solutions of Class 11th Chapter 3 Trigonometric Functions:

Q1. Find the radian measures corresponding to the following degree measures:

(i) 25° (ii) – 47°30′ (iii) 240° (iv) 520°

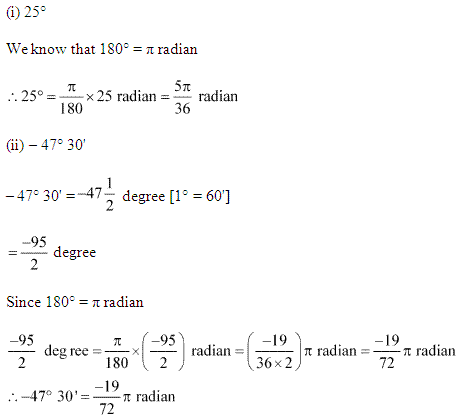
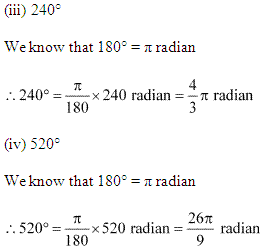
Q2. Find the degree measures corresponding to the following radian measures (Use π=22/7).

(i) 11/16 (ii)-4 (iii) 5π/3 (iv) 7π/6

A.2. (i) 11/16

We know that radian= 180°,

Hence, 11/16 radian= 11/16 × 180°/π = 11/16 × 180°/22/7 = 11/16 × 7/22 ×180 °

= 315/8°

=39° 3°/8

= 39 °+ 3 ×6°/8 minute (as 1 °=60′)

=39°+22′+ 12′

=39°+22′+ 60/2” (as 1′=60”)

=39°+22′+30”.

=39° 22′ 30”.

(ii) -4

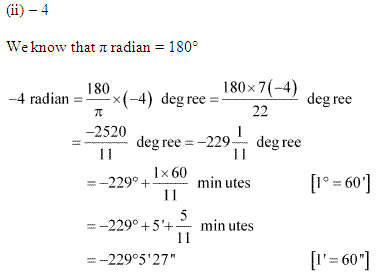
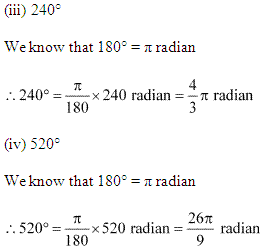
Q3. A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?

A.3. Given that a wheel makes 360 revolutions in one minute

Then, number of revolutions in one second = 360/60 =6.

In 1 complete revolution the wheel turns 360°= 2π radian.

So, In 6 revolution, the wheel will turns 6×2π radian = 12π radian.

Hence, in one second the wheel will turn an angle of 12π radian.

Q4. Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm (Use π=22/7).

A.4. Here l = 22cm.

r =100cm. Ø = ?

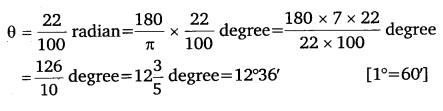
Q5. In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.
Ans:

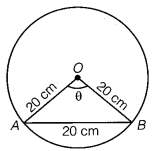
Given, diameter = 40 cm
∴ radius (r) = 40/2 = 20 cm
and length of chord, AB = 20 cm
Thus, ∆OAB is an equilateral triangle.
We know that,
θ = Arc AB/ radius
⇒ Arc AB = θ × r
= π/3 × 20 .
= 20/3 π cm.

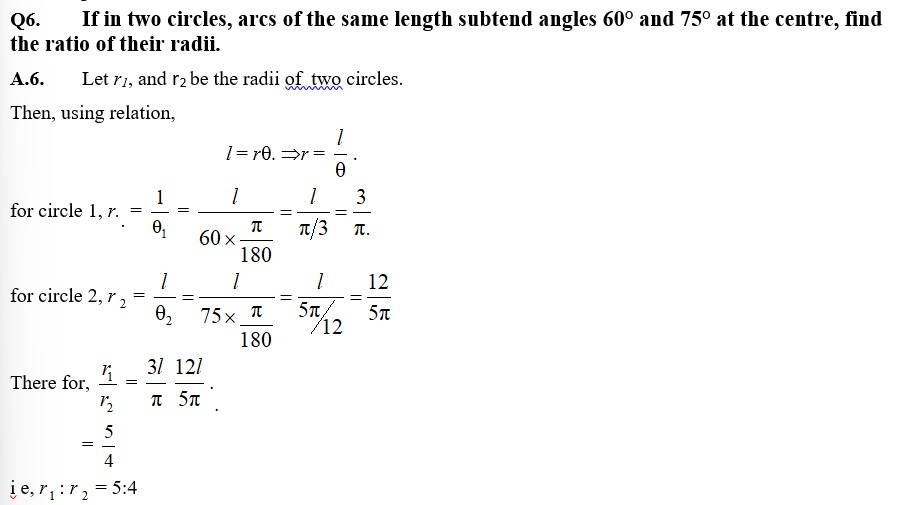
Q7. Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length

(i) 10 cm (ii) 15 cm (iii) 21 cm

A.7. Here,

r= length of pendulum.

r= 75 cm.

then
θ = l/r.

(i)Are of length, l = 10 cm

θ = 10/75 radian
= 2/15 radian

(ii) Here, l = 15 cm
θ = 15/75 radian
θ = 1/5 radian

(iii) Here, l = 21 cm
θ = 21/75 radian
= 7/25 radian.

Q1. Find the values of other five trigonometric functions if –

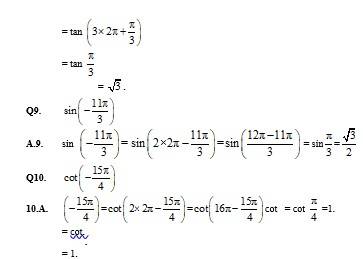
Q1. Prove that: sin² π/6 + cos² π/3 – tan² π/4 = – 12
Ans: L.H.S.= sin² π/6 + cos² π/3 – tan² π/4

= (1/2)²+(1/2)² – (1)²

= 1/4+/41=−1/2

= R.H.S.
Q2. Prove that: 2 sin² π/6 + cosec² 7π/6 cos² π/3 = 3/2

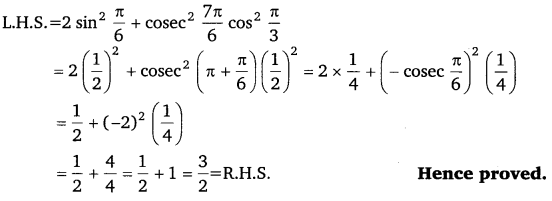
Q3. Prove that : cot² π/6 + cosec 5π/6 + 3 tan² π/6 = 6

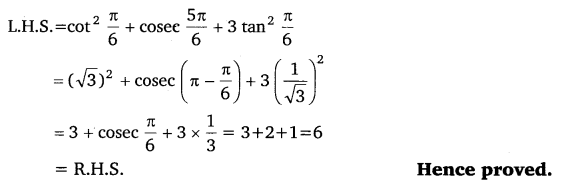
Q4. Prove that: 2 sin² 3π/4 + 2 cos² π/4 + 2 sec² π/3 = 10

Ans. L.H.S = 2sin²3π/4+2cos²π/4+2sec²π/3

Here. Sin 3π/4 = Sin ( 4π – π /4 )

= 2{sin(π−π/4)}²+2(1/√2)²+ 2(2)²

= 2{sinπ/4}²+2×1/2+8

= 2 (1/√2)² + 1 + 8

= 1 + 1 + 8
= 10 = R.H.S.

Q5. Find the value of:

(i) sin 75° (ii) tan 15°
Ans:

(i) sin 75°

sin (45° + 30°)
= sin 45° cos 30° + cos 45° sin 30°
[∵ sin (x + y) = sin x cos y + cos x sin y]
= (1/√2)(√3/2)+(1/√2)(1/2)

= √3/2√2+1/2√2 =√3+1/2√2

(ii) tan 15° = tan (45° – 30°)

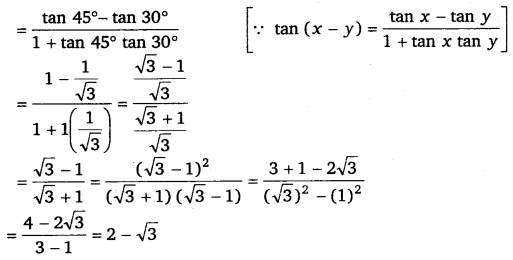
Q6. cos(π/4−x) cos(π/4−y)−sin(π/4−x)sin(π/4−y) = sin (x + y)

Ans:

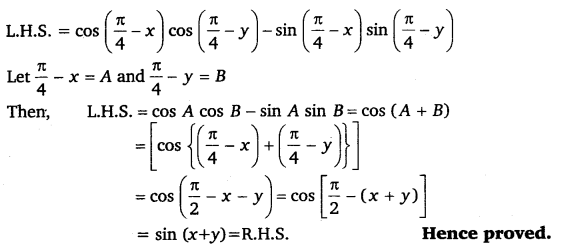
Q7. Prove that: tan(π/4+x) / tan(π/4−x)= (1+tanx1−tanx)²

Ans:

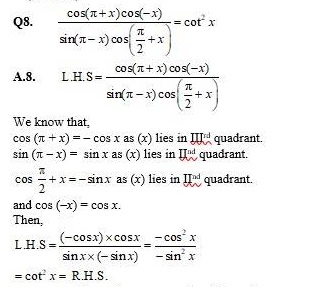
Q.9

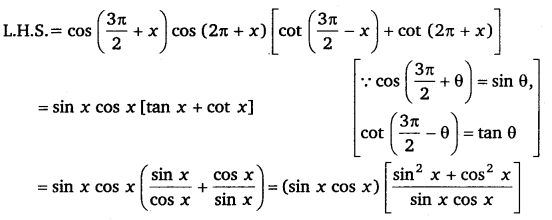
= 1 = R.H.S

Q10. Prove that: sin (n + 1) x sin (n + 2) x + cos (n + 1) x cos (n + 2) x = cos x
Ans:
L.H. S. = sin (n + 1 )x sin (n + 2) x + cos (n +1) x cos (n + 2) x
[By the formula, cos (A – B) = cos A cos B + sin A sin B]
= cos [(n + 2) x + (n + 1) x]
= cos (4x + 2x – 4x – x)
= cos x = R.H.S.

Q11. Prove that: cos(3π/4+x)−cos(3π/4−x)=–√2sinx
Ans: It is known that
cos A – cos B = −2sin(A+B/2)⋅sin(A−B/2)

∴ L.H.S.= =cos(3π/4+x)−cos(3π/4−x)

= –2sin{(3π/4+x)+(3π/4−x)2}⋅sin{(3π/4+x)−(3π/4−x)2}

= – 2 sin (3π/4) sin x

= – 2 sin (- π/4) sin x

= – √2 sin x = R.H.S.

Q12. Prove that: sin² 6x – sin² 4x = sin 2x sin 10 x
Ans: It is known that
sin A + sin B = 2 sin(A−B/2)cos(A−B/2)

sin A – sin B = 2 cos(A+B/2)sin(A−B/2)
L.H.S.= sin² 6x – sin² 4x
= (sin 6x + sin 4x) (sin 6x – sin 4x)
= (2 sin 5x cos x) (2 cos 5x sin x)
= (2 sin 5x cos 5x) (2 sin x cos x)
= sin 10x sin 2x = R.H.S.

Q13. Prove that: cos² 2x cos² 6x = sin 4x sin 8x
Ans: It is known that
cos A + cos B = 2 cos(A+B/2)cos(A−B/2)

cos A – cos = 2 sin(A+B/2)sin(A−B/2)

∴ L.H.S = cos² 2x – cos² 6x
= (cos 2x + cos 6x) (cos 2x – 6x)
= [2cos(2x+6x/2)cos(2x−6x/2)][−2sin(2x+6x/2)sin(2x−6x/2)]
∴ L.H.S.= cos² 2x – cos² 6x
= (cos 2x + cos 6x) (cos 2x – 6x)
= [2 cos 4x cos (-2x)] [- 2 sin 4x sin (- 2x)]
= [2 cos 4x cos 2x] [- 2 sin 4x (- sin 2x)]
= (2 sin 4x cos 4x) (2 sin 2x cos 2x)
= sin 8x sin 4x
= R.H.S.

Q14. Prove that: sin 2x + 2 sin 4x + sin 6x = 4 cos² x sin 4x
Ans:
L.H.S.= sin 2x + 2 sin 4x + sin 6x
= [sin 2x + sin 6x] + 2 sin 4x
= [2sin(2x+6x/2)cos(2x−6x/2)] + 2 sin 4x
[∵ sin A + sin B = 2 sin(A+B/2)cos(A−B/2)]
= 2 sin 4x cos (- 2x) + 2 sin 4x
= 2 sin 4x cos 2x + 2 sin 4x
= 2 sin 4x (cos 2x + 1)
= 2 sin 4x (2 cos² x – 1 + 1)
= 2 sin 4x (2 cos² x)
= 4 cos² x sin 4x
= R.H.S.

Q15. cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x)

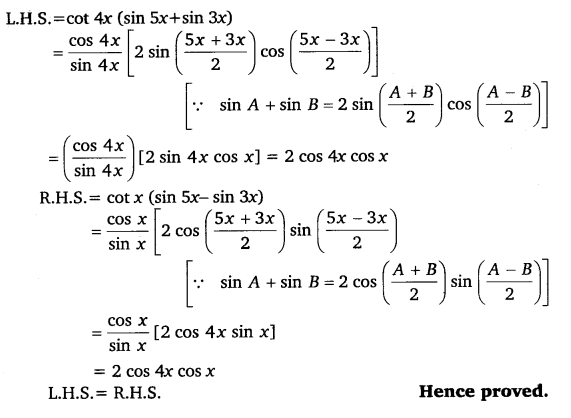
Q16. Prove that: cos9x−cos5x / sin17x−sin3x=−sin2x / cos10x

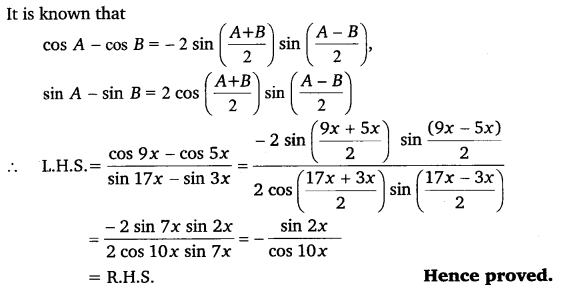
Q17. Prove that: $\frac{\sin 5 x + \sin 3 x}{\cos 5 x + \cos 3 x}$ = tan 4x
Ans: It is known that
sin A + sin B = 2 $\sin (\frac{A + B}{2}) \cos (\frac{A - B}{2})$

cos A + cos = 2 $\cos (\frac{A + B}{2}) \cos (\frac{A - B}{2})$

∴ L.H.S = $\frac{\sin 5 x + \sin 3 x}{\cos 5 x + \cos 3 x}$

= $\frac{2 \sin (\frac{5 x + 3 x}{2}) \cos (\frac{5 x - 3 x}{2})}{2 \cos (\frac{5 x + 3 x}{2}) \cos (\frac{5 x - 3 x}{2})}$

= $\frac{2 \sin 4 x \cos x}{2 \cos 4 x \cos x} = \frac{\sin 4 x}{\cos 4 x}$

= tan 4x = R.H.S.

Q18. Prove that:

$\frac{\sin x - \sin y}{\cos x + \cos y} = \tan \frac{x - y}{2}$

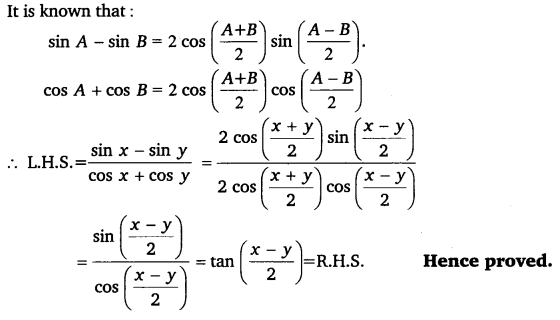
Q19. Prove that:

$\frac{\sin x + \sin 3 x}{\cos x + \cos 3 x}$ = tan 2x

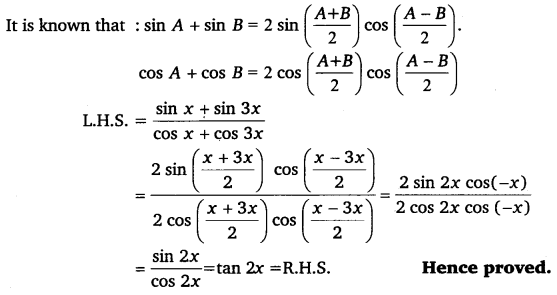
Q20. Prove that:

$\frac{\sin x - \sin 3 x}{\sin^{2} x - \cos^{2} x}$ = 2 sin x

It is known that
sin A – sin B = 2 $\cos (\frac{A + B}{2}) \sin (\frac{A - B}{2})$

cos² A – sin² A = cos 2A

∴ L.H.S. $= \frac{\sin x - \sin 3 x}{\sin^{2} x - \cos^{2} x}$

= $\frac{2 \cos (\frac{x + 3 x}{2}) \sin (\frac{x - 3 x}{2})}{- \cos 2 x}$

= $\frac{2 \cos 2 x \sin (- x)}{- \cos 2 x}$

= – 2 × (- sin x) = 2 sin x

= R.H.S

Q21. Prove that: $\frac{\cos 4 x + \cos 3 x + \cos 2 x}{\sin 4 x + \sin 3 x + \sin 2 x}$ = cot 3x

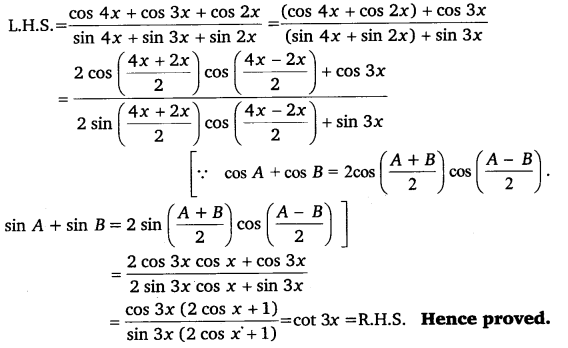
Q22. Prove that : cot x cot 2x – cot 2x cot 3x – cot 3x cot x = 1
Ans:
L.H.S.= cot x cot 2x – cot 2x cot 3x – cot 3x cot x
= cot x cot 2x – cot 3x (cot 2x + cot x)
= cot x cot 2x – cot (2x + x) (cot 2x + cot x)
= cot x cot 2x – $[\frac{\cot 2 x \cot x - 1}{\cot x + \cot 2 x}]$ (cot 2x + cot x)
[∵ cot (A + B) = $\frac{\cot A \cot B - 1}{\cot A + \cot B}$ ]
= cot x cot 2x – (cot 2x cot x – 1)
= 1 = R.H.S.

Q23. tan 4x = $\frac{4 \tan x (1 - \tan^{2} x)}{1 - 6 \tan^{2} x + \tan^{4} x}$

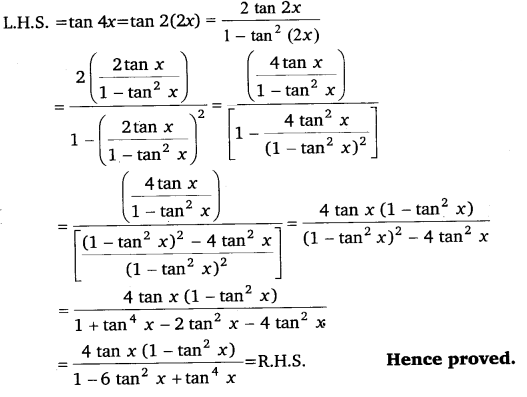
Q24. Prove that: cos 4x = 18 sin² x cos² x
Ans:
L.H.S. = cos 4x = cos 2(2x)
= 1 – 2 sin² 2x [∵ cos 2A = 1 – 2 sin² A]
= 1 – 2(2 sin x cos x)² [∵ sin 2A = 2 sin A cos A]
= 1 – 8 sin² x cos² x
= R.H.S.

Q25. Prove that: cos 6x = 32 cos⁶ x – 48 cos⁴ x + 18 cos² x – 1
Ans:
We know that: cos 3x = 4 cos³ x – 3cos x
On replacing x by 2x, we get
cos 3(2x) = 4 cos³ (2x) – 3 cos 2x
⇒ cos 6x = 4 (2cos² x – 1)³ – 3 (2cos² x – 1)
[∵ cos 2x = 2cos² x – 1]
= 4 [8 cos⁶ x – 12 cos⁴ x + 6 cos² x – 1] – 6 cos² x + 3
[∵ (a – b)³ = a³ – 3a²b + 3ab² – b³]
= 32 cos⁶ x – 48 cos⁴ x + 24 cos² x – 4 – 6 cos² x + 3
⇒ cos 6x = 32 cos⁶ x – 48 cos⁴ x + 18 cos² x – 1

sin 6x/2 sin 2x/2 = 0

sin 3x sin x = 0.

sin 3x = 0 or sin x = 0

3x = nπ or x = nπ, n € z

Q6. cos 3x + cos x – cos 2x = 0

A.6. We have,

cos 3x + cosx-cos 2x = 0.

(cos 3x + cosx) – cos 2x = 0

Using cos A + cos B = 2 cos A+B/2 cos A-B/2

2 cos (3x+x/2) cos (3x−x/2) – cos 2x = 0.

2 cos 4x/2 cos 2x/2 – cos 2x = 0

2 cos 2xcosx – cos 2x = 0

cos 2x. (2 cosx – 1) = 0.

cos 2x = 0 or 2 cosx -1 = 0.

2x = (2n + 1) π/2 , n∈z or cosx = 1/2 = cos π/3

x = (2n + 1) π/4 , n∈z or x = 2nx± π/3 , n∈z.

Q7. sin 2x + cos x = 0

A.7. We have,

sin 2x + cosx = 0.

2 sin cosx + cosx = 0( ∵ sin 2x = 2 sin xcosx)

cosx (2 sin x + 1) = 0.

cosx = 0 or 2 sinx + 1 = 0.

x = (2n + 1) π/2 , n∈z or sin x = 1/2 = -sin π/6 = sin π + π/6= sin 7π/6.

x = (2n + 1) π/2 , x∈z or x= nπ + (-1)ⁿ 7π/6, n∈z.

Q8. sec²2x = 1– tan 2x

A.8. We have,

sec² 2x = 1 tan 2x

1 + tan² 2x = 1 tan 2x[ sec²x = 1 + tan²x]

tan² 2x + tan 2x = 0.

tan 2x (tan 2x + 1) = 0.

tan 2x = 0 or tan 2x + 1 = 0.

2x = nπ, x∈z or tan 2x = -1 = -tan π/4 = tan π- π/4 = tan 3π/4.

x= nπ/2 , n∈z or 2x = nπ + 3π/4 , n∈z.

x = nπ/2+3π/8, n∈z

Q9. sin x + sin 3x + sin 5x = 0

A.9. We have,

sinx + sin 3x + sin 5x = 0.

(sinx + sin 5x) + sin 3x = 0.

Using sin A + sin B = 2 sin A+B/2 cos A−B/2 .

2 sin (x+5x/2) cos (x−5x/2) + sin 3x = 0.

2 sin 6x/2 cos -4x/2 + sin 3x = 0.

2 sin 3xcos (-2x) + sin 3x = 0.

sin 3x [2 cos 2x + 1] = 0[ ∵ cos (-x) = cosx].

sin 3x = 0 or 2 cos 2x + 1 = 0.

3x = nπ, n∈z. or cos 2x = -1/2 = -cos π/3 = cos π – π/3= cos 2π/3

x= nπ/3 , n∈z or 2x = 2nπ± 2π/3 .

x = nπ± π/3 , n∈z.

NCERT Solutions Maths Chapter 3 Trigonometric Functions For Class 11

NCERT Solutions of Class 11th Chapter 3 Trigonometric Functions:

CBSE Classes

Competitive Exams

Useful Links

News and Updates

© 2024 Edu-Spot : All Rights Reserved |