NCERT Solutions Maths Chapter 4 Principle of Mathematical Induction for Class 11
Chapter 4 of NCERT Mathematics for Class 11, titled “Principle of Mathematical Induction,” introduces one of the fundamental techniques in mathematics used to prove statements or formulas. The principle of mathematical induction is based on the idea of proving that if a statement is true for the first natural number (usually 1), and if we assume it is true for an arbitrary natural number k, we can then prove that it is true for k+1. This method is often used to prove statements that are true for all natural numbers or integers within a certain range. The process involves two main steps: the base case (proving the statement for the smallest number, usually 1), and the inductive step (assuming the statement is true for k and proving it for k+1). This technique is essential in various fields of mathematics, including algebra, number theory, and combinatorics, and serves as a powerful tool to establish the truth of infinite sequences or series.
NCERT Solutions Maths Chapter 4 Principle of Mathematical Induction For Class 11
Q1. 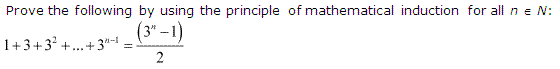
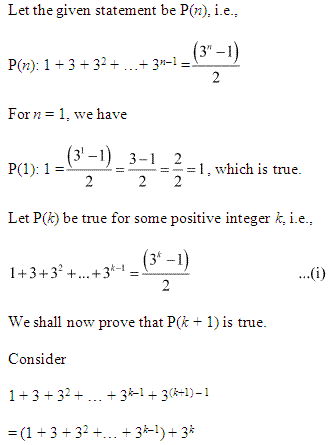

Q2. 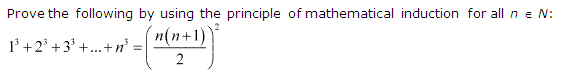
Let the given statement be P(n), i.e.,
P(n) = 13 + 23 + 33 + …………. + n3 = (n(n+1)/2)²
For n = 1, we have
P(1) : 13 = 1
= (1(1+1)/2)²=(1×2/2)²
= 12 = 1 which is true.
Let P(k) be true for some positive integer k, i.e.,
13 + 23 + 33 + …………. + k3 = (k(k+1)/2)²
We shall now prove that P(k+1) is true.
Consider 13 + 23 + 33 + …………. + k3 = (k(k+1)/2)²

Q3. 
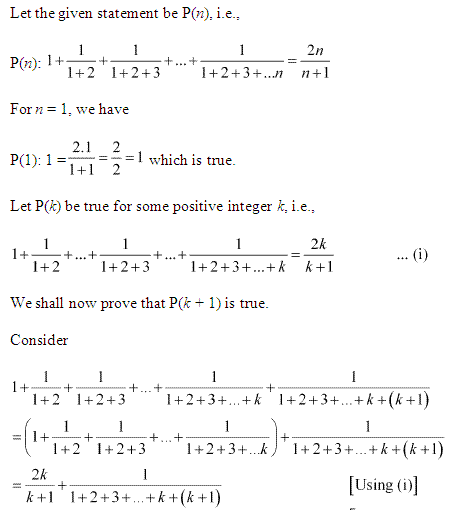

Q4. 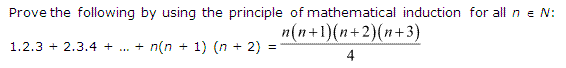


Q.5 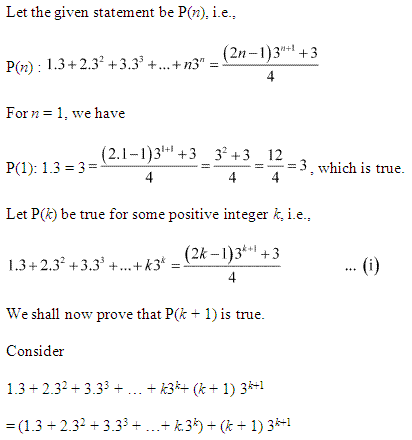

Q.6 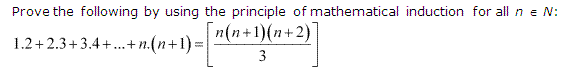

k(k+1)(k+2) /3 + (k + 1) (k + 2)
= (k + 1) (k + 2) + (k/3 + 1)
= (k+1)(k+2)(k+3)/3
= (k+1)(k+1+1)(k+1+2)/3
Thus, P(k+1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q7. 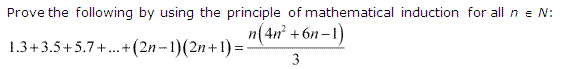
Let the given statement be P(n), i.e.,
P(n) : 1 . 3 + 3 . 5 + 5 . 7 + … + (2n – 1) (2n + 1) = n(4n²+6n−1) /3
For n = 1, we have
P(1) : 1 . 3 = 3
= 1(4.1²+6.1−1) /3
=4+6−1 /3=9/3 = 3, which is true.
Let P(k) be true for some positive integer k, Le.,
1 . 3 + 3 . 5 + 5 . 7 + ………………. + (2k – 1) (2k + 1) = k(4k²+6k−1)/3 ……………(i)
We shall now prove that P(k + 1) is true.
Consider (1 . 3 + 3 . 5 + 5 . 7 + … + (2k – 1) (2k + 1) +{2 (k + 1) – 1} {2(k + 1) + 1}
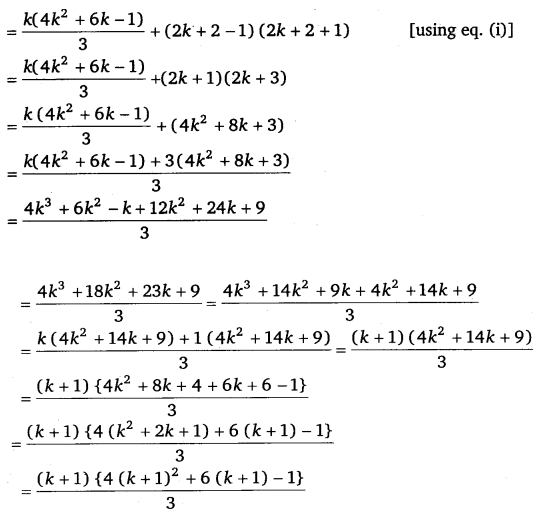
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, .statement P(n) is true for all natural numbers i.e., n.
Q8. ![]()

Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, .statement P(n) is true for all natural numbers i.e., n.
Q9. 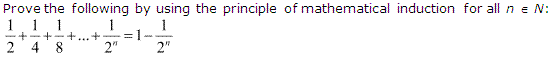
Ans : Let the given statement be P(n), i.e.,
P(n) : ![]()
For n = 1, we have
P(1) : 1/2
= 1 – 1/2¹
= 1/2, which is true.
Let P(k) be true for some positive integer k, i.e.,
1/2+1/4+1/8+…+1/![]() =1−1/
=1−1/![]()
We shall now prove that P(k + 1) is true.
Consider (1/2+1/4+1/8+…+1/![]() )+1 /
)+1 /![]()
= (1−1/![]() )+1/
)+1/![]()
= 1−1/![]() +1/2.
+1/2.![]() =1−1/
=1−1/![]() (1−1/2)1−12k+122k
(1−1/2)1−12k+122k
= 1−1/![]() (1/2)=1−1/
(1/2)=1−1/![]()
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q10. 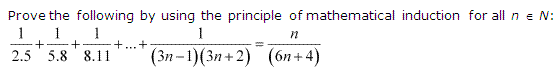
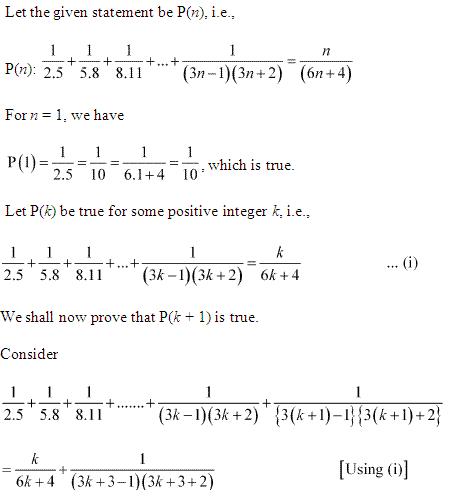
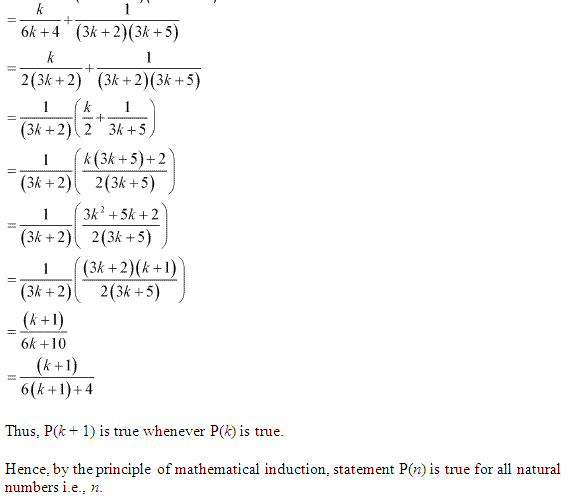
Q11. 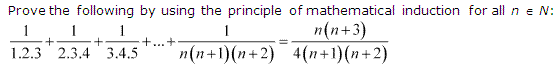
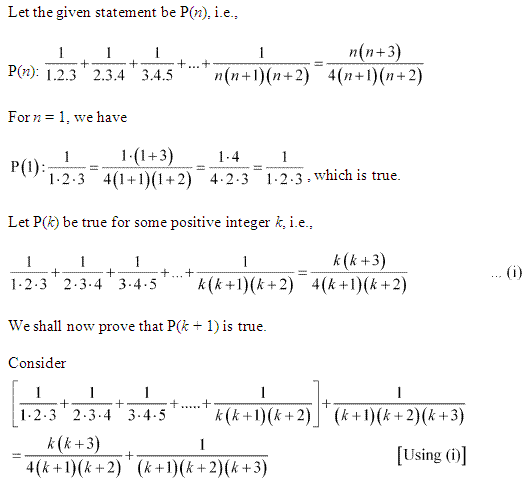
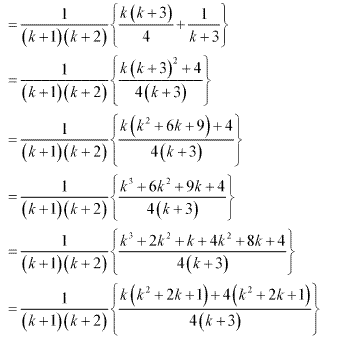

Q12. 
Let the given statement be P(n), i.e.,
P(n) : a + ar + ar2 + …………… + arn – 1 = a(rn−1)r−1
For n = 1, we have
P(1) : a = a(r1−1)(r−1)a(r1−1)/(r−1) = a, which is true.
Let P(k) be true for some positive integer k, i.e.,
a + ar + ar2 + …………… + ark – 1 = a(rk−1)/r−1 …………..(i)
We shall now prove that P(k + 1) is true.
Consider
a + ar + ar2 + …………… + ark – 1} + ar(k + 1) – 1 = a(rk−1) /r−1 [Using eQuestion (i)]
= a(rk−1)+ark(k−1) /r−1
= a(rk−1)+ark+1−ark /r−1
= ark−a+ark+1−ark /r−1=ark+1−a /r−1
= a(rk+1−1) /r−1
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q13. 
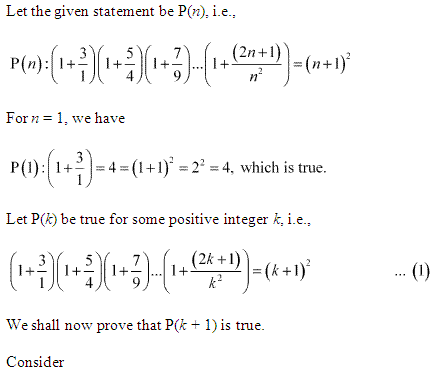

Q14. 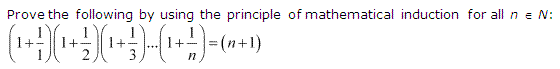

Q15. Prove the following by using the principle of mathematical indcution for all n ∈ N:
12 + 32 + 52 + … + (2n – 1)2 = n(2n−1)(2n+1 )/3
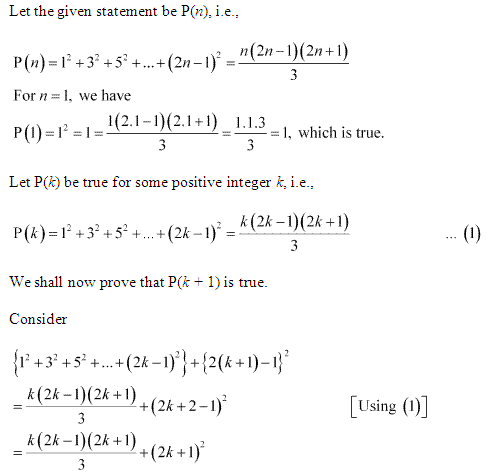

Q16. 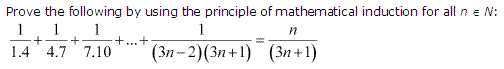


Q17. 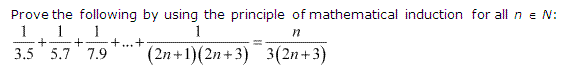


Q18. 

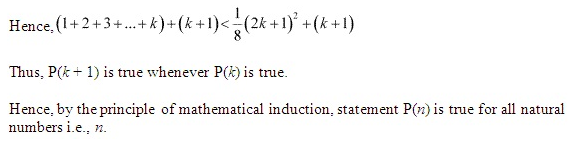
Q19. ![]()
Ans : Let the given statement be P(n), i.e.,
P(n) : n (n + 1) (n + 5) which is a multiple of 3.
It can be noted that P(n) is true for n=l since 1 (1 + 1) (1 + 5) = 12, which is a multiple of 3.
Let P(k) be true for some positive integer k, i.e., k (k + 1) (k + 5) is a multiple of 3.
∴ k (k + 1) (k + 5) = 3m, where m ∈ N ……………….(i)
We shall now prove that P(k + 1) is true whenever P(k) is true.
Consider (k + 1) {(k +1 ) + 1} {(k + 1) + 5}
= (k + 1) (k + 2) {(k + 5) + 1}
= (k + 1) (k + 2) (k + 5) + (k + 1) (k + 2)
= {k (k + 1) (k + 5) + 2 (k + 1) (k + 5)} + (k +1) (k + 2)
= 3m + (k + 1) {2 (k + 5) + (k + 2)}
= 3m + (k + 1) {2k +10 + k + 2}
= 3m + (k + 1) (3k + 12)
= 3m + 3 (k + 1) (k + 4)
= 3 {m + (k + 1) (k + 4)}
= 3 × q, where, q = {m + (k +1) (k + 4)} is some natural number.
Therefore, (k +1) {(k +1) +1} {(k +1) + 5} is a multiple of 3.
Thus, P(k + 1) is trtie whenever P(k) is true.
Hence, by the principle of mathematical induction, statement P(n) is true for all natural numbers i.e., n.
Q20. ![]()


Q21. ![]()


Q22. ![]()

Q23. ![]()
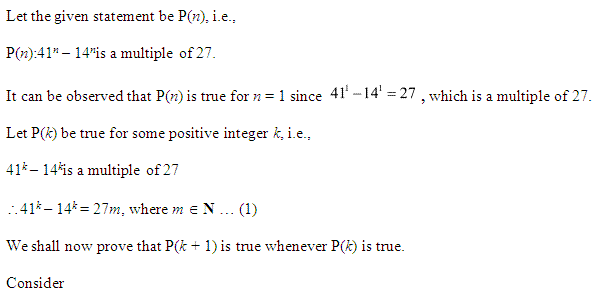

Q24. 


