NCERT Solutions Maths Chapter 7 Permutations and Combinations for Class 11
1. How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5, assuming that
(i) Repetition of the digits is allowed?
(ii) Repetition of the digits is not allowed?
Solution:
(i) Let the 3-digit number be ABC, where C is at the units place, B at the tens place and A at the hundreds place.
Now, when repetition is allowed,
The number of digits possible at C is 5. As repetition is allowed, the number of digits possible at B and A is also 5 at each.
Hence, the total number possible 3-digit numbers =5 × 5 × 5 =125
(ii) Let the 3-digit number be ABC, where C is at the units place, B at the tens place and A at the hundreds place.
Now, when repetition is not allowed,
The number of digits possible at C is 5. Suppose one of 5 digits occupies place C; now, as the repletion is not allowed, the possible digits for place B are 4, and similarly, there are only 3 possible digits for place A.
Therefore, the total number of possible 3-digit numbers=5 × 4 × 3=60
2. How many 3-digit even numbers can be formed from the digits 1, 2, 3, 4, 5, and 6 if the digits can be repeated?
Solution:
Let the 3-digit number be ABC, where C is at the unit’s place, B at the tens place and A at the hundreds place.
As the number has to be even, the digits possible at C are 2 or 4 or 6. That is, the number of possible digits at C is 3.
Now, as repetition is allowed, the digits possible at B is 6. Similarly, at A, also, the number of digits possible is 6.
Therefore, The total number of possible 3-digit numbers = 6 × 6 × 3 = 108
3. How many 4-letter codes can be formed using the first 10 letters of the English alphabet, if no letter can be repeated?
Solution:
Let the 4-letter code be 1234.
In the first place, the number of letters possible is 10.
Suppose any 1 of the ten occupies place 1.
Now, as repetition is not allowed, the number of letters possible at place 2 is 9. Now, at 1 and 2, any 2 of the 10 alphabets have been taken. The number of alphabets left for place 3 is 8, and similarly, the number of alphabets possible at 4 is 7.
Therefore, the total number of 4-letter codes=10 × 9 × 8 × 7=5040
4. How many 5-digit telephone numbers can be constructed using the digits 0 to 9 if each number starts with 67 and no digit appears more than once?
Solution:
Let the five-digit number be ABCDE. Given that the first 2 digits of each number are 67. Therefore, the number is 67CDE.
As repetition is not allowed and 6 and 7 are already taken, the digits available for place C are 0,1,2,3,4,5,8,9. The number of possible digits at place C is 8. Suppose one of them is taken at C; now the digits possible at place D is 7. And similarly, at E, the possible digits are 6.
∴ The total five-digit numbers with given conditions = 8 × 7 × 6 = 336
5. A coin is tossed 3 times, and the outcomes are recorded. How many possible outcomes are there?
Solution:
Given A coin is tossed 3 times, and the outcomes are recorded.
The possible outcomes after a coin toss are head and tail.
The number of possible outcomes at each coin toss is 2.
∴ The total number of possible outcomes after 3 times = 2 × 2 × 2 = 8
6. Given 5 flags of different colours, how many different signals can be generated if each signal requires the use of 2 flags, one below the other?
Solution:
Given 5 flags of different colours.
We know the signal requires 2 flags.
The number of flags possible for the upper flag is 5.
Now, as one of the flags is taken, the number of flags remaining for the lower flag in the signal is 4.
The number of ways in which signal can be given = 5 × 4 = 20
1. Evaluate
(i) 8!
(ii) 4! – 3!
Solution:
(i) Consider 8!
We know that 8! = 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
= 40320
(ii) Consider 4!-3!
4!-3! = (4 × 3!) – 3!
The above equation can be written as
= 3! (4-1)
= 3 × 2 × 1 × 3
= 18
2. Is 3! + 4! = 7!?
Solution:
Consider LHS 3! + 4!
Computing the left-hand side, we get
3! + 4! = (3 × 2 × 1) + (4 × 3 × 2 × 1)
= 6 + 24
= 30
Again, considering RHS and computing, we get
7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040
Therefore, LHS ≠ RHS
Therefore, 3! + 4! ≠ 7!
Q3. Compute
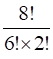
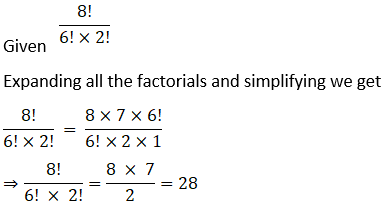
Q4. 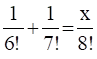
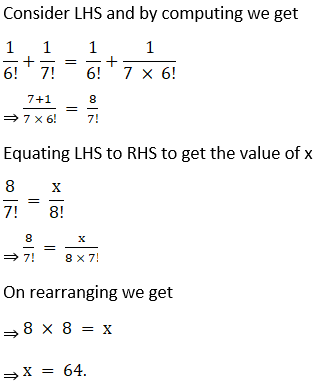
Q5. 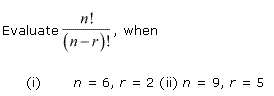
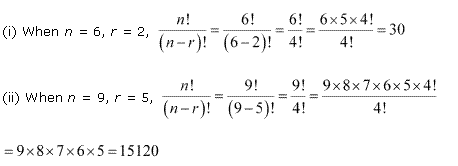
Q1. How many 3-digit numbers can be formed by using the digits 1 to 9 if no digit is repeated?

Q.2 How many 4-digit numbers are there with no digit repeated?
To find the four-digit number (digits do not repeat),
We will have 4 places where 4-digits are to be put.
So, at the thousand’s place = There are 9 ways as 0 cannot be at the thousand’s place = 9 ways
At the hundredth’s place = There are 9 digits to be filled as 1 digit is already taken = 9 ways
At the ten’s place = There are now 8 digits to be filled as 2 digits are already taken = 8 ways
At unit’s place = There are 7 digits that can be filled = 7 ways
The total number of ways to fill the four places = 9 × 9 × 8 × 7 = 4536 ways
So, a total of 4536 four-digit numbers can be there with no digits repeated.
Q3. How many 3-digit even numbers can be made using the digits 1, 2, 3, 4, 6, 7, if no digit is repeated?
An even number means that the last digit should be even.
The number of possible digits at one’s place = 3 (2, 4 and 6)
⇒ Number of permutations=![]()
One of the digits is taken at one’s place; the number of possible digits available = 5
⇒ Number of permutations=![]()
Q4. Find the number of 4-digit numbers that can be formed using the digits 1, 2, 3, 4, 5, if no digit is repeated. How many of these will be even?
Total number of digits possible for choosing = 5
Number of places for which a digit has to be taken = 4
As there is no repetition allowed,
⇒ Number of permutations =![]()
The number will be even when 2 and 4 are in one’s place.
The possibility of (2, 4) at one’s place = 2/5 = 0.4
The total number of even numbers = 120 × 0.4 = 48
Q5. From a committee of 8 persons, in how many ways can we choose a chairman and a vice chairman, assuming one person cannot hold more than one position?
Total number of people in committee = 8
Number of positions to be filled = 2
⇒ Number of permutations =![]()
Q6. ![]()

Q7. ![]()
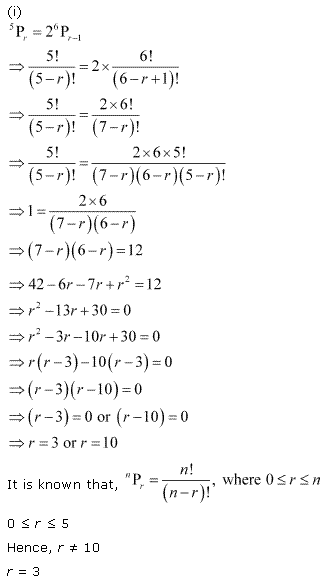
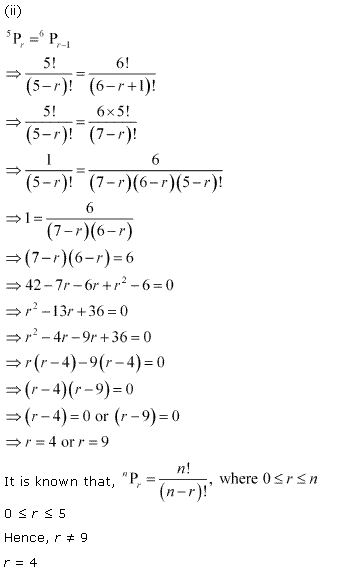
Q8. How many words, with or without meaning, can be formed using all the letters of the word EQUATION, using each letter exactly once?
Total number of different letters in EQUATION = 8
Number of letters to be used to form a word = 8
⇒ Number of permutations =![]()
Q9. How many words, with or without meaning, can be made from the letters of the word MONDAY, assuming that no letter is repeated, if.
(i) 4 letters are used at a time,
(ii) All letters are used at a time,
(iii) All letters are used, but the first letter is a vowel.

Q10. In how many of the distinct permutations of the letters in MISSISSIPPI do the four I’s not come together?
Total number of letters in MISSISSIPPI =11

Q11.


Q1. ![]()
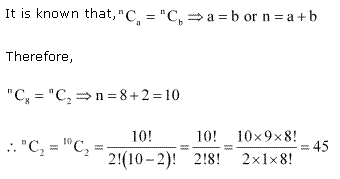
Q2. 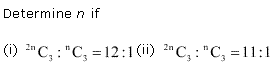

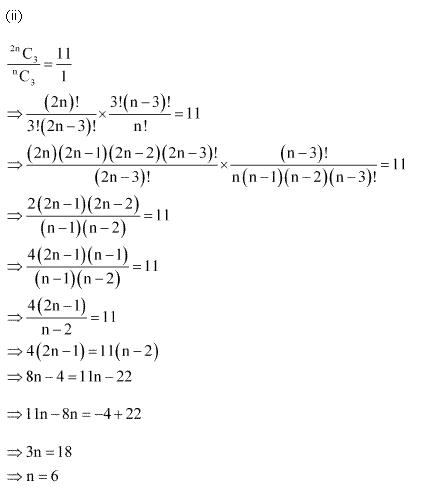
Q3. How many chords can be drawn through 21 points on a circle?
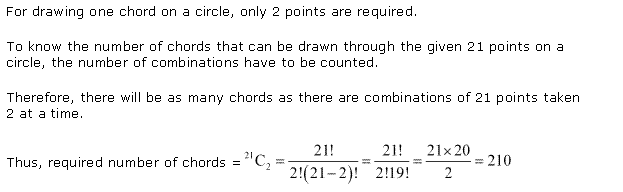
Q4. In how many ways can a team of 3 boys and 3 girls be selected from 5 boys and 4 girls?

Q5. Find the number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls if each selection consists of 3 balls of each colour.

Q6. Determine the number of 5 card combinations out of a deck of 52 cards if there is exactly one ace in each combination.

Q7. In how many ways can one select a cricket team of eleven from 17 players in which only 5 players can bowl if each cricket team of 11 must include exactly 4 bowlers?

Q8. A bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected.
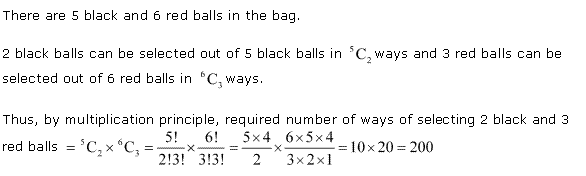
Q9. In how many ways can a student choose a programme of 5 courses if 9 courses are available and 2 specific courses are compulsory for every student?

