Sample Question Paper
Mathematics-Basic
Class X – Session 2019-20
Section – A
Q1. If an event that cannot occur, then its probability is: [1]
Solution: An event that cannot occur has 0 probability, such an event is called impossible event.
Q2. Which of the following is not a zero of the polynomial p(x) = x3 - 7x + 6 [1]
Solution: Here, p(1) = (1)3 - 7(1) + 6 = 0
p(2) = (2)3 - 7(2) + 6 = 0
p(-2) = (-2)3 - 7(-2) + 6 ≠ 0
p(-3) = (-3)3 - 7(-3) + 6 = 0
So, -2 is not a zero of p(x).
Q3. It is proposed to build a single circular park equal in area to the sum of areas of two circular parks of diameters 16 m and 12 m in a locality. The radius of the new park would be: [1]
Solution: Area of first circular park whose diameter is 16 m,
=![]() (16/2)2
(16/2)2
= ![]() (8)2
(8)2
=64![]() m2
m2
Area of second circular park whose diameter is 12 m,
=![]() (12/2)2
(12/2)2
= ![]() (6)2
(6)2
=36![]() m2
m2
According to question,
Area of single circular park = Area of first circular park + Area of second circular park
![]() (r)2 = 36
(r)2 = 36![]() m2 + 64
m2 + 64![]() m2
m2
r2 = 100
r = 10 m
Q4. Which term of the AP: 4, 9, 14, ...... is 254? [1]
Solution: Here, a = 4 and d = 5
Let nth term of the AP be 254. Then,
an = a + (n - 1) d
⇒ 254 = 4 + (n - 1) (5)
⇒ 5(n - 1) = 250
⇒ n = 51
Q5. A man goes 15 m due west and then 8 m due north. Now far is he from the starting point? [1]
Solution:
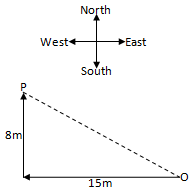
op2=152+ 82
op2=225 +64
op2=289
op= 17m
Q6. In figure, a circle with center O is inscribed in a quadrilateral ABCD such that, it touches the sides BC,AB, AD and CD at points P, Q, R and S respectively. If AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5cm, then the radius of the circle (in cm.) is: [1]
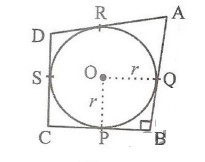
Solution:
Since DS = DR = 5 cm
(tangents of a circle from same external point)
Now, AR = AD - DR = 25 - 5 = 18 cm
Similarly, AR = AQ = 18 cm (tangents)
Now, QB = AB - AQ = 29 - 18 = 11 cm
Similarly, QB = PB = 11 cm
Given, ∠B = 90°
So, ∠POQ = 90°
Hence, OQBP is square
QB = 11 cm
Side of square = 11 cm, so the radius = 11 cm.
Q7. The sum of the first 20 natural numbers is ......... [1]
Solution: Sum of first 20 natural numbers=
20 x (20+1) / 2 = 210
Q8. The value of 3cosec2A - 3cot2A is ........... [1]
Solution: 3cosec2A - 3cot2A
= 3 (cosec2A - cot2A)
= 3 x 1 = 3
Q9. Find the least number that is divisible by all the numbers from 1 to 10 (both inclusive): [1]
Solution:
Required number = LCM (1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
= 1 × 2 × 2 × 2 × 3 × 3 × 5 × 7
= 2520
Q10. Find the distance of the point (-4, -7) from the y-axis. [1]
Points are(-4, -7) and (0, -7)
Distance = √(0 +4)2 ( -7 +7)2
=√ 42+ 02
=√ 16
= 4 units
Section - B
Q1. Explain whether 3 × 12 × 101 + 4 is a prime number or a composite number. [2]
Solution:
3 × 12 × 101 + 4
= 4(3 × 3 × 101 + 1)
= 4(909 + 1)
= 4(910)
= 2 × 2 × 2 × 5 × 7 × 13
= a composite number
[∵ Product of more than two prime factors]
Q2. Find the zeros of the polynomial p(x) = 12 + x - x2
x2 - x - 12
x2 - 4x + 3x - 12
x(x-4) + 3(x-4)
(x+3)(x-4)
So, the two zeros are 4 and -3
Q3. Find the value of k for which the roots of the quadratic equation 2x2 + kx + 8 = 0 will have the equal roots?
For equal roots, D = 0
b2 - 4ac
b2 = 4ac
k2 = 4 x 2 x 8
k2 = 64
k = +√64
k = +8 or k = -8
Q4. Two unbiased coins are tossed. Find the probability of getting: [2]
(i) two heads
(ii) at least one head.
Solution:
No. of possible outcomes = 4
(i) No. of favourable outcomes = 1
namely HH {Sample space S = {HH, HT, TH, TT}}
So, required probability = 1/4
(ii) No. of favourable outcomes = 3, namely {HH, HT, TH}
So, required probability = 3/4
Q5. Solve for x and y:
3x + 2y = 11, 2x + 3y = 4
Solution:
Given equations are:
3x + 2y = 11 .....(i)
2x + 3y = 4 ......(ii)
Eq. (ii) gives, y = (4-2x)/3……(iii)
Substituting this value of y in Eq. (i), we have
3x + {2(4-2x)/3} = 11
9x + 8 - 4x = 33
5x = 25
x = 5
Substituting this value of x in Eq. (iii), we have:
y = 4 - 2x5/3
y = -2
Thus, x = 5, y = -2



