Note: As per the revised CBSE curriculum, this chapter has been removed from the syllabus for the 2020-21 academic session.
The area represents the amount of planar surface being covered by a closed geometric figure.

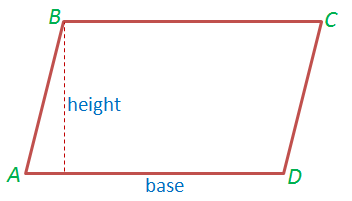
Area of a parallelogram
The area of a parallelogram is the product of any of its sides and the corresponding altitude.
Area of a parallelogram = b×h
Where ‘b′ is the base and ‘h′ is the corresponding altitude(Height).
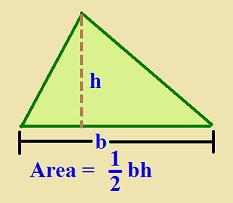
Area of a triangle
Area of a triangle = (1/2)×b×h
Where “b” is the base and “h” is the corresponding altitude.
Theorems
Parallelograms on the Common Base and Between the Same Parallels
Theorem: Parallelograms that lie on the common base and between the same parallels are said to have equal in area.
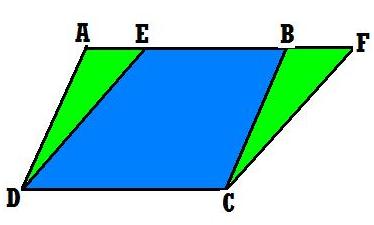
Two parallelograms are said to be on the common/same base and between the same parallels if
a) They have a common side.
b) The sides parallel to the common side lie on the same straight line.
Triangles on the Common Base and Between the Same Parallels
Theorem: Triangles that lie on the same or the common base and also between the same parallels are said to have an equal area.
Here, ar(ΔABC)=ar(ΔABD)
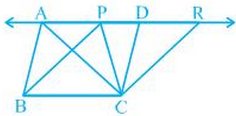
Two triangles are said to be on the common base and between the same parallels if
a) They have a common side.
b) The vertices opposite the common side lie on a straight line parallel to the common side.
Two Triangles Having the Common Base & Equal Areas
If two triangles have equal bases and are equal in area, then their corresponding altitudes are equal.
A Parallelogram and a Triangle Between the Same parallels
Theorem: If a triangle and a parallelogram are on the common base and between the same parallels, then the area of the triangle is equal to half the area of the parallelogram.
A triangle and a parallelogram are said to be on the same base and between the same parallels if
a) They have a common side.
b) The vertices opposite the common side lie on a straight line parallel to the common side.


