CBSE 9th Maths

Basic Terms and Definitions
(i) Line segment: A part of a line with two endpoints is called a line segment.

Line segment AB is denoted by .
(ii) Ray: A part of a line with one endpoint is called a ray.

The ray AB is denoted by .
(iii) Collinear points and non-collinear points: If three or more than three points he on the same line, then they are called collinear points, otherwise, they are non-collinear points.

P, Q and R are collinear points.

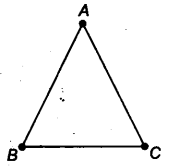
A, B and C are non-collinear points.

A, B and C are non-collinear points.

2. Angle: An angle is formed when two rays originate from the same endpoint.

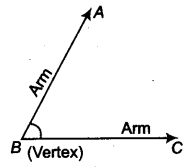
Angle ABC is denoted by ∠ABC
The rays ( and ) making an angle are called the arms of ∠ABC.
The end point (B) is called the vertex of ∠ABC.

Types of Angles: There are different types of angles such as acute angle, right angle, obtuse angle, straight angle and reflex angle.
(i) Acute angle: An acute angle is an angle which is less than 90°.
Acute angle : 0° < x < 90°.

(ii) Right angle: A right angle is an angle which is equal to 90°.
Right angle : y = 90°

(iii) Obtuse angle: An obtuse angle is an angle which is more than 90° and less than 180°.
Obtuse angle : 90° < z < 180°

(iv) Straight angle: A straight angle is an angle which is equal to 180°.

(v) Reflex angle: A reflex angle is an angle, which is more than 180° and less than 360°.
Reflex angle : 180° < t < 360°

Complementary Angles: Two angles whose sum is 90° are called complementary angles.

Supplementary Angles: Two angles whose sum is 180° are called supplementary angles.

Adjacent Angles: Two angles are adjacent if they have a common vertex, a common arm and their non-common arms are on different sides of the common arm.
∠ABD and ∠DBC are the adjacent angles. Ray BD is their common arm and point B is their common vertex. Ray BA and ray BC are non-common arms.

Vertically Opposite Angles: The vertically opposite angles formed when two lines intersect each other at a point.