1. Triangle: A plane figure bounded by three line segments is called a triangle.
In ΔABC has
(i) three vertices, namely A, B and C.
(ii) three sides, namely AB, BC and CA.
(iii) three angles, namely ∠A, ∠B and ∠C.
2. Types of Triangle on the Basis of Sides
(i) Equilateral triangle: A triangle having all sides equal is called an equilateral triangle.
In equilateral ΔABC,
i.e., AB = BC = CA
(ii) Isosceles triangle: A triangle having two sides equal is called an isosceles triangle.
In isosceles ΔABC,
i.e., AB = AC
(iii) Scalene triangle: A triangle in which all the sides are of different lengths is called a scalene triangle.
In scalene ΔABC,
i.e., AB ≠ BC ≠ CA
3. The perimeter of a Triangle: The sum of the lengths of three sides of a triangle is called its perimeter.
Let, AB = c, BC = a, CA = b
i.e., Perimeter of ΔABC, 2s = a + b + c
4. Area of a Triangle: The measure of the surface enclosed by the boundary of the triangle is called its area.
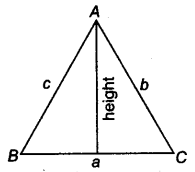
Area of triangle = 1/2 × Base × Height
Area of right angled triangle = 1/2 × Base × Perpendicular
5. Area of a Triangle (Heron’s Formula): If a triangle has a, b and c as sides, then the area of a triangle by Heron’s formula = s(s−a)(s−b)(s−c)−−−−−−−−−−−−−−−−−−√
where, s (semi-perimeter) = a+b+c2
Note: This formula is highly applicable in the case when we don’t have the exact idea about height.
6. Application of Heron’s Formula in Finding Areas of Quadrilaterals: Let ABCD he a quadrilateral to find the area of a quadrilateral we need to divide the quadrilateral in triangular parts.

Area of quadrilateral ABCD = Area of ΔABC + Area of ΔADC
ncert solutions


