CBSE Class 7th Maths

Introduction to Numbers

Natural Numbers : The collection of all the counting numbers is called set of natural numbers. It is denoted by N = {1,2,3,4….}

Whole Numbers: The collection of natural numbers along with zero is called a set of whole numbers. It is denoted by W = { 0, 1, 2, 3, 4, 5, … }

Properties of Addition and Subtraction of Integers

Closure under Addition and subtraction
For every integer $a$ and $b$,  $a+b$ and $a–b$ are integers.

Commutativity Property for addition
for every integer $a$ and $b$,  $a+b=b+a$

Associativity Property for addition
for every integer $a$,$b$ and $c$, $(a+b)+c=a+(b+c)$

Additive Identity & Additive Inverse

Additive Identity
For every integer $a$, $a+0=0+a=a$ here 0 is Additive Identity, since adding 0 to a number leaves it unchanged.
Example : For an integer 2, 2+0 = 0+2 = 2.

Additive inverse
For every integer $a$, $a+(-a)=0$ Here, $-a$ is additive inverse of $a$ and $a$ is the additive inverse of-a.
Example : For an integer 2, (– 2) is additive inverse  and for (– 2), additive inverse is 2. [Since + 2 – 2 = 0]

Properties of Multiplication of Integers

Properties of Multiplication of Integers

Closure under Multiplication
For every integer $a$ and $b$, $a\times b=Integer$

Commutative Property of Multiplication
For every integer $a$ and $b$, $a\times b=b\times a$

Multiplication by Zero
For every integer $a$, $a\times 0=0\times a=0$

Multiplicative Identity
For every integer $a$, $a\times 1=1\times a=a$. Here 1 is the multiplicative identity for integers.

Associative property of Multiplication
For every integer $a$, $b$  and $c$,  $(a\times b)\times c=a\times (b\times c)$

Distributive Property of Integers
Under addition and multiplication,  integers show the distributive property.
i.e., For every integer $a$, $b$  and $c$,  $a\times (b+c)=a\times b+a\times c$

These properties make calculations easier.

Division of Integers

When a positive integer is divided by a positive integer, the quotient obtained is a positive integer.
Example: (+6) ÷ (+3) $=+2$

When a negative integer is divided by a negative integer, the quotient obtained is a positive integer.
Example: (-6) ÷ (-3) $=+2$

When a positive integer is divided by a negative integer or negative integer is divided by a positive integer, the quotient obtained is a negative integer.
Example: (-6) ÷ (+3) $=-2$ and Example: (+6) ÷ (-3) $=-2$

Number Line

Representation of integers on a number line

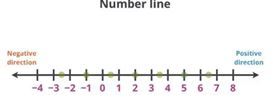
On a number line when we add a positive integer for a given integer, we move to the right, add a negative integer for a given integer, we move to the left.