CBSE Class 7th Maths

Construction of Triangles

1. Properties of triangles

• The exterior angle of a triangle is equal in measure to the sum of interior opposite angles.
• The total measure of the three angles of a triangle is 180°.
• Sum of the lengths of any two sides of a triangle is greater than the length of the third side.
• In any right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.

2. Essential measurements for the construction of a triangle
A triangle can be drawn if any one of the following sets of measurements is given:

• Three sides: SSS
• Two sides and the angle between them: SAS
• Two angles and the side between them: ASA
• The hypotenuse and a leg in the case of a right-angled triangle: RHS

Steps of construction of a line parallel to a given line

1. Take a line $l$ and a point A outside $l$.
2. Take any point B on $l$ and join it to A.

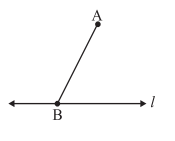
3. With B as the centre and a convenient radius, cut an arc on $l$ at C and BA at D.

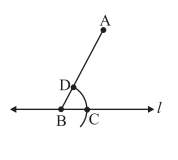
4. With A as the centre and same radius as in Step 3, cut an arc EF to cut AB at G.

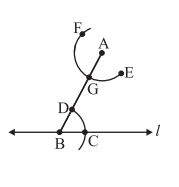
5. Measure the arc length CD by placing pointed tip of the compass at C and pencil tip opening at D.

6. With this opening, keep G as centre and draw an arc to cut arc EF at H

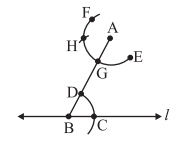
7. Join AH to draw a line $m$

∠ABC and ∠BAH are alternate interior angles. Therefore, $m$ || $l$

Construction of a triangle :

Construction of a triangle with SSS criterion.

Construct a triangle ABC, given that AB = 5 cm, BC = 6 cm and AC = 7 cm.
Steps:

1. 1. Make a rough sketch for your reference
   2. Draw a line segment BC = 6 cm

Step 1: First, we draw a rough sketch with a given measure.

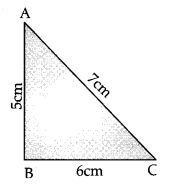
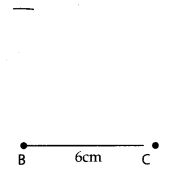
Step 2: Draw a line segment BC of length 6 cm.

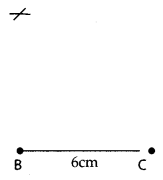
Step 3: From B, point A is at a distance of 5 cm. So with B as centre, draw an arc of radius 5 cm.

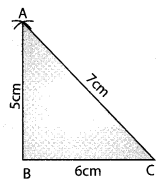
Step 4: From C, point A is at a distance of 7 cm. So, with C as centre, draw an arc of radius 7 cm.

Step 5: A has to be on both the arcs drawn. So, it is the point of intersection of arc.
Mark the point of intersection of arcs as A. Join AB and AC. ΔABC is now ready.

Construction of a triangle with SAS criterion

• Construct ΔPQR with QR = 7.5 cm, PQ = 5 cm and ∠Q = 60$0^{}$.
  Steps:
  1. Make a rough sketch for your reference
  2. Draw a line segment QR = 7.5 cm

3. At Q, draw QX making 60$0^{}$ with QR

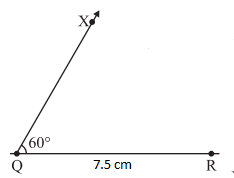
4. With Q as centre, draw an arc of radius 5 cm. It cuts QX at P.

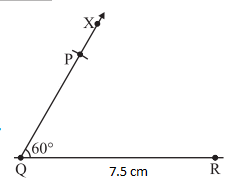
5. Join AB. ΔPQR is now ready

Construction of a triangle with ASA criterion

Steps of Construction
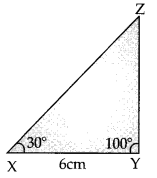
Step 1: Before actual construction, we draw a rough sketch with measures marked on it.

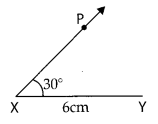
Step 2: Draw XY of length 6 cm.

Step 3: At X, draw a ray XP making an angle of 30° with XY. By the given condition Z must be somewhere on the XP.

Step 4: At Y, draw a ray YQ making an angle of 100° with YX. By the given condition, Z must be on the ray YQ also.

Step 5: Z has to lie on both the rays XP and YQ. So, the point of intersection of two rays is Z.

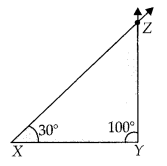
ΔXYZ is now completed.

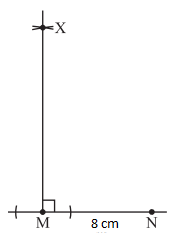
Construction of a triangle with RHS criterion

• Construct ΔLMN, where ∠M = 90$0^{}$, MN = 8cm and LN = 10 cm.
  Steps:
  1. Make a rough sketch for your reference
  2. Draw MN = 8 cm

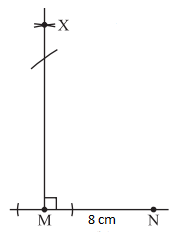
3. At M, draw MX ⊥ MN.

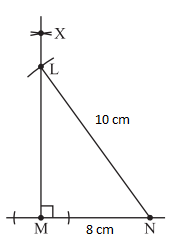
4. With N as centre, draw an arc of radius 10 cm to cut MX at L

5. Join LN.

6. ΔLMN is now completed

 

NCERT Solutions