The number of the 
e.g. 
is a fraction, where 3 is numerator and 5 is denominator.
A fraction whose numerator is less than its denominator is called a proper fraction.
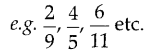
A fraction whose numerator is more than or equal to its denominator is called an improper fraction.
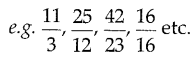
A number which can be expressed as the sum of a natural number and a proper fraction is called a mixed fraction.
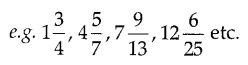
Fractions having the same denominator but different numerators are called like fractions.
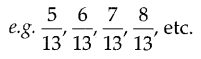
Fractions having different denominator are called, unlike fractions.
Multiplication of Fractions
There arise many situations when we have to multiply two fractions. For example: to calculate the area of a rectangle with given length and breadth.
Multiplication of a Fraction by a Whole Number
To multiply a whole number with a proper or an improper fraction, we multiply the whole number with the numerator of the fraction, keeping the denominator same.
Multiplication of a mixed fraction to a whole number: To multiply a mixed fraction by a whole number, we first convert the mixed fraction to an improper fraction and then multiply.
Fraction as an operator ‘of’ indicates multiplication.
Product of two whole numbers: The product of two whole numbers is bigger in size than each of the two whole numbers. For example, 3 x 4 = 12 and 12 > 4, 12 > 3.
Product of two proper fractions: When two proper fractions are multiplied, the product is less than both the fractions or, we say the size of the product of two proper fractions is smaller than the size of each of the two fractions.
Division of the Whole Number by a Fraction
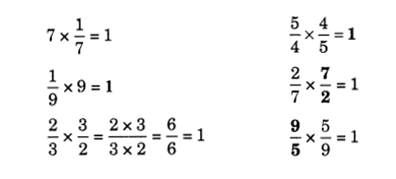
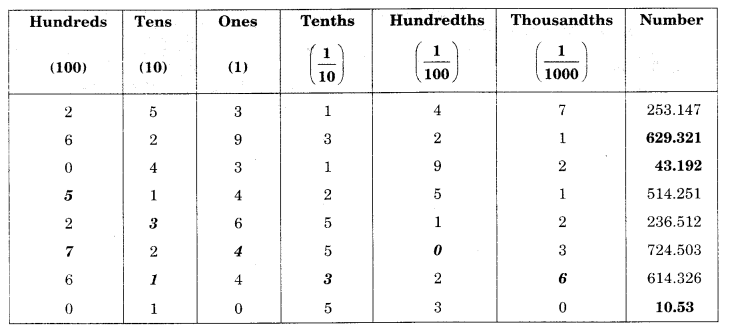
Decimal number and its expanded form
Need of decimals: While converting lower units of money, length, and weight, to their higher units, we are required to use decimals. For example,
3 paise = ₹ 0.03
5 g = 0.005 kg
7 cm = 0.07 m.
Addition and subtraction of decimals: We are already familiar with how to add and subtract decimals.
Thus, 21.36 + 37.35 is 58.71
Multiplication of Decimal Numbers by 10, 100 and 1000
(i) Decimal numbers as a fraction with denominator 10 or 100 or 1000, etc.
We observe that,
2.3 = 
(ii) Multiplication of a decimal by 10 or 100 or 1000
Let us look at the following table:
1.7 × 10 = 17.0 or 17
1.7 × 100 = 170.0 or 170
1.7 × 1000 = 1700.0 or 1700
2.35 × 10 = 23.5
2.35 × 100 = 235.0 or 235
2.35 × 1000 = 2350.0 or 2350
We observe that in 1.7 × 10 = 17.
The digits in the number 1.7 and product 17 are same,
i.e., 1 and 7 and 0 is decimal in 17,
i.e., 17.0 is placed one digit to the right as compared to its placement in 17.
Note that 10 has one zero.
The observation is the same in the other products involving 10, in the table.
In 1.7 × 100 = 170, the digits in 1.7 (i.e., 1.70) and 170 are same,
i.e., 1, 7 and 0.
The decimal in the product 170 (i.e., 170.0) is placed two digits to the right as compared so its position in 1.70.
Note that 100 has two zeros.
The observation is the same in the other products involving 100 in the table.
In 1.7 × 1000 = 1700, the digits in 1.7 (i.e., 1.700) and 1700 are same,
i.e., 1, 7 and 0.
The decimal in the product 1700 (i.e., 1700.0) is placed three digits to the right as compared to its position in 1.700.
Note that 1000 has three zeros.
The observation is the same in the other products involving 1000 in the table.
Result: When we multiply a number by 10 or 100 or 1000, we get a product in which the digits are the same as in the number itself, but the decimal is shifted to the right by one digit (for multiplication by 10), by two digits (for multiplication by 100) and by three digits (for multiplication by 1000).
Thus, 1.92 × 10 = 19.2
1.92 × 100 = 192
1.92 × 1000 – 1.920 × 1000 = 1920.
