CBSE 9th Science

Distance and Displacement

The magnitude of the length covered by a moving object is called distance. It has no direction.

Displacement is the shortest distance between two points or the distance between the starting and final positions with respect to time. It has magnitude as well direction.

Displacement can be zero, but distance cannot.

Magnitude

Magnitude is the size or extent of a physical quantity. In physics, we have scalar and vector quantities.

Scalar quantities are only expressed as magnitude. E.g: time, distance, mass, temperature, area, volume

Vector quantities are expressed in magnitude as well as the direction of the object. E.g: Velocity, displacement, weight, momentum, force, acceleration, etc.

Time, Average Speed and Velocity

Time and speed

Time is the duration of an event that is expressed in seconds. Most physical phenomena occur with respect to time. It is a scalar quantity.

Speed is the rate of change of distance. If a body covers a certain distance in a certain amount of time, its speed is given by

Speed = DistanceTime

Average speed = Total distance travelled / Total time taken

Uniform motion and non-uniform motion

When an object covers equal distances in equal intervals of time it is in uniform motion.

When an object covers unequal distances in equal intervals of time it is said to be in non-uniform motion.

Velocity

The Rate of change of displacement is velocity. It is a vector quantity. Here the direction of motion is specified.

Velocity =  DisplacementTime

Average velocity = (Initial Velocity + Final velocity)/2 = u+v2.

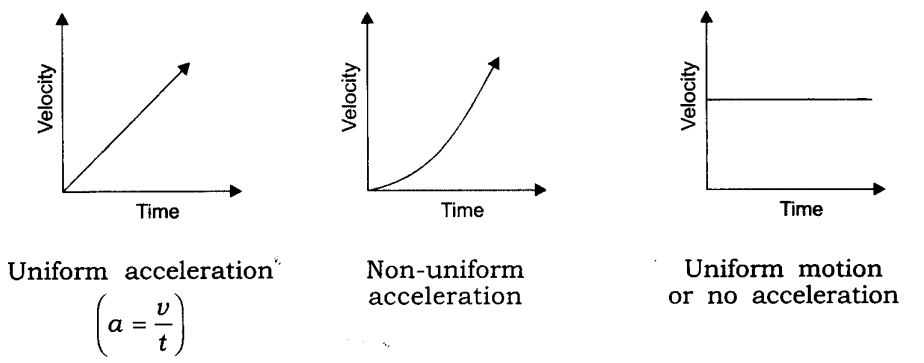
Acceleration

The rate of change of velocity is called acceleration it is a vector quantity. In non-uniform motion,
velocity varies with time, i.e., change in velocity is not 0. It is denoted by “a”

$Acceleration=$Change in Velocity / Time  (OR)  a = vut

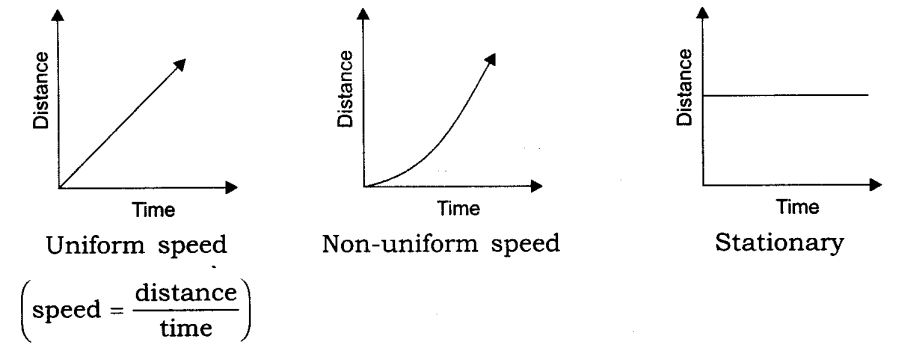
Distance-Time graph

• Distance-Time graphs show the change in position of an object with respect to time.
• Linear variation = uniform motion and non-linear variations imply non- uniform motion
• The slope gives us speed

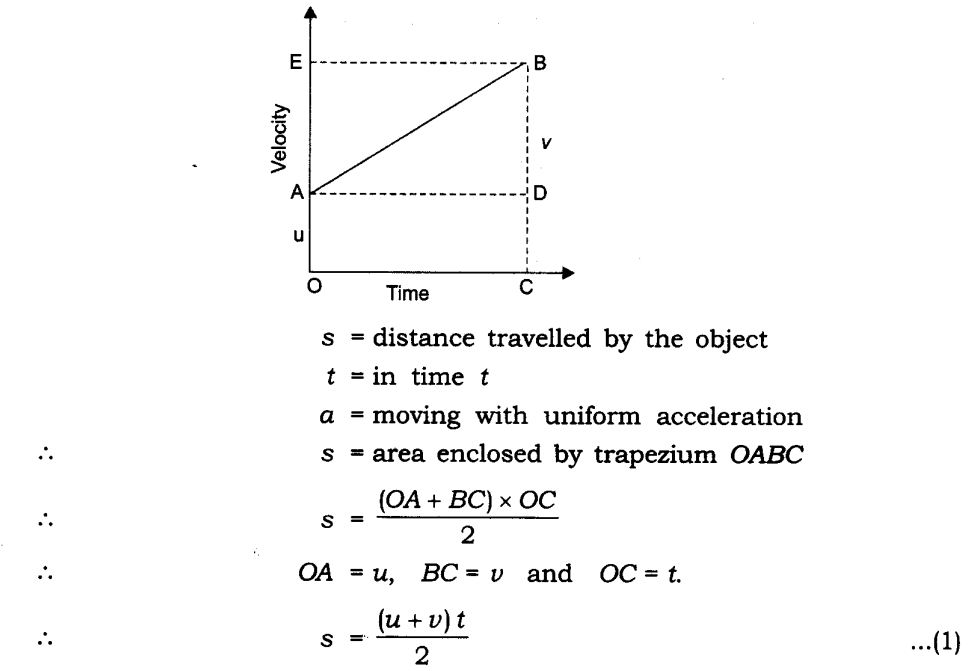
(ii) Velocity-time graph

 

Equations of Motion

The motion of an object moving at uniform acceleration can be described with the help of three equations, namely

(i) v = u + at

(ii) v² – u² = 2as

(iii) s = ut + (1/2)at²

Derivation of velocity-time relation by graphical method

(i)velocity-time relation:

 

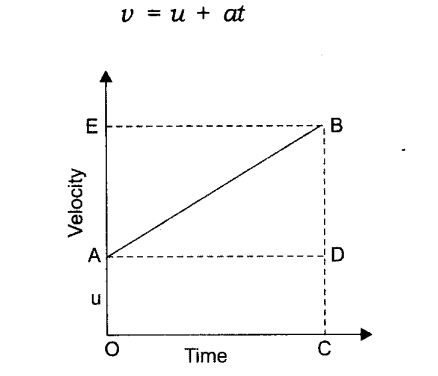
A body starts with some initial non-zero velocity at A and goes to B  with constant acceleration a.

From the graph BD = v (final velocity) – DC = u (initial velocity)…………..(eq 1).

BD = BC – DC……………..(eq 2).

We know acceleration a = slope = BDAD or AD = OC = t (time taken to reach point B).

$Therefore$ BD = at………………….(eq 3).

Substitute everything  we get : at = v – u.

Rearrange to get v = u + at.

Derivation of position-time relation by graphical method

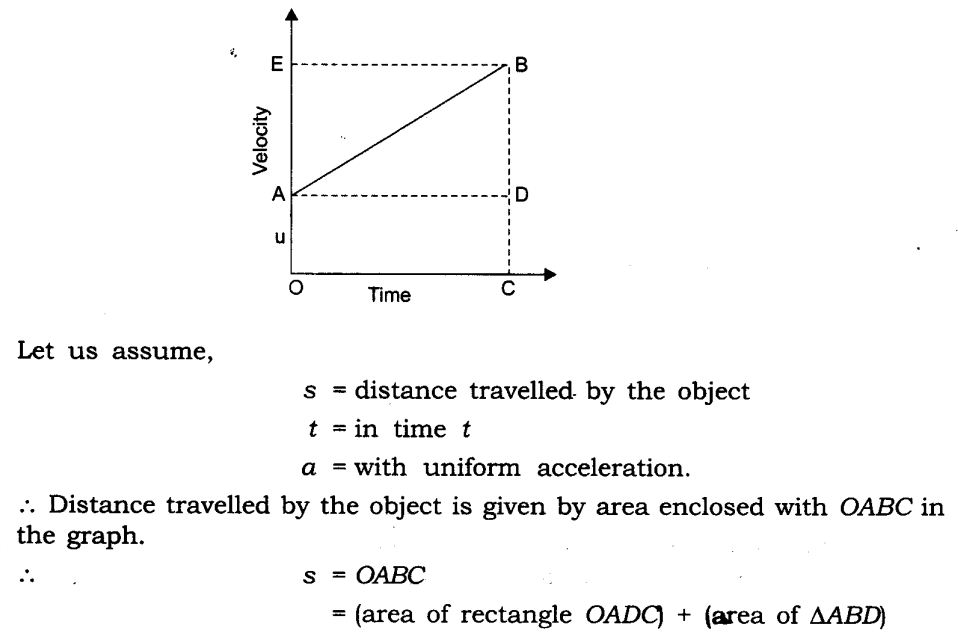
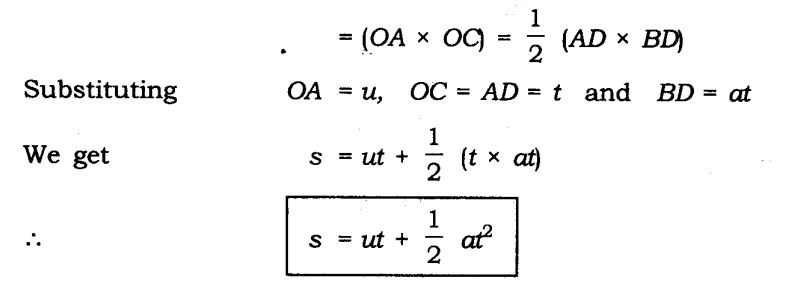
Derivation of position-velocity relation by graphical method

 

 

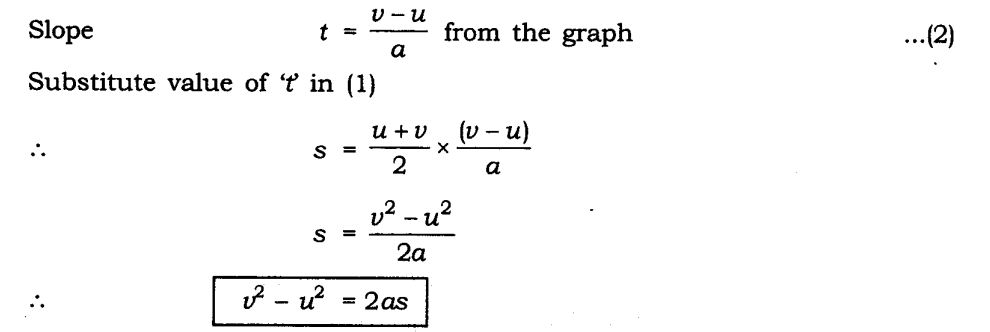
ncert Textbook solutions