The numbers which are involved in many mathematical applications such as addition, subtraction and multiplication which are inherently closed with many mathematical processes are called Rational numbers.
Rational Numbers
A number is called rational if we can write the number in the form of , where p and q are integers and q ≠ 0
i.e., 1 = , 2 =
, 0 =
and
,
,
are all rational numbers.
Between two rational numbers x and y, there exists a rational number
Properties of Rational Numbers
(i) Closure Property
Rational numbers are closed under :
Addition
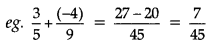
which is a rational number.

are rational numbers.
Multiplication:

are rational numbers.
Rational numbers are closed under addition subtraction and multiplication.
Division : eq. , which is also a rational number. For any rational number a, a ÷ 0 is not defined. So, rational number are not closed under division.
However, if we exclude zero then the rational numbers are closed under division.
(ii) Commutativity:
Addition: Two rational numbers can be added in any order, i.e., commutativity holds for rational numbers under addition, i.e., for any two rational number a and b, a + b = b + a.
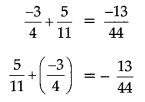
Subtraction:
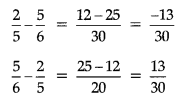
(iii) Multiplication: Multiplication is commutative for rational numbers. In general, a × b = b × a, for any two rational numbers a and b.
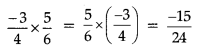
Division:
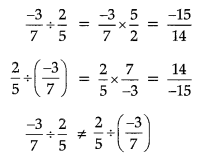
(iii) Associativity:
For any three rational numbers a,b and c, (a∗b)∗c=a∗(b∗c). i.e., Associative property is one where the result of an equation must remain the same despite a change in the order of operators. Given three rational numbers a,b and c, it can be said that : (a+b)+c = a+(b+c). Therefore addition is associative. (a−b)−c≠a−(b−c). Because (a-b)-c = a-b-c whereas a-(b-c) = a-b+c. Therefore we can say that subtraction is not associative. (a×b)×c=a×(b×c). Therefore multiplication is associative.(a÷b)÷c≠(a÷b)÷c. Therefore division is not associative.
The numbers 1, 2, 3, 4, ………. are called natural numbers.
If we add 0 to the collection of natural numbers, what we get is called the collection of whole numbers.
Thus, 0, 1, 2, 3, 4, are whole numbers.
Natural numbers are also known as positive integers. If we put a negative sign before each positive integer, we get negative integers. Thus, -1, -2,
-3, -4, ………. are negative integers. A number of the form , where p and q are integers and q ≠ 0 is called a rational number. All the above types of numbers are needed to solve various types of simple algebraic equations.
Properties of Rational Numbers
The list of properties of rational numbers can be given as follows:
- Closure
- Commutativity
- Associativity
- The role of zero (0)
- The role of 1
- Negative of a number
- Reciprocal
- Distributivity of multiplication over addition for rational numbers.
Distributivity of Multiplication Over Addition for Rational Numbers
For all rational numbers a, b and c,
a(b + c) = ab + ac
a(b – c) = ab – ac.
Representation of Rational Numbers on the Number Line

- We draw a line.
- We mark a point O on it and name it 0. Mark a point to the right of 0. Name it 1. The distance between these two points is called unit distance.
- Mark a point to the right of 1 at unit distance and name it 2.
- Proceeding in this manner, we can mark points 3, 4, 5,
- Similarly we can mark – 1, – 2, – 3, – 4, – 5, ……… to the left of 0. This line is called the number line.
- This line extends indefinitely on both sides.
The positive rational numbers are represented by points on the number line to the right of O whereas the negative rational numbers are represented by points on the number line to the left of O.
Any rational number can be represented on this line. The denominator of the rational number indicates the number of equal parts into which the first unit has been divided whereas the numerator indicates as to how many of these parts are to be taken into consideration.
Rational Numbers Between Two Rational Numbers
We can find infinitely many rational numbers between any two given rational numbers. We can take the help of the idea of the mean for this purpose.


