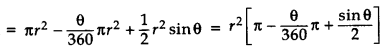Circumference of a circle = 2πr
Area of a circle = πr2 …[where r is the radius of a circle]
Area of a semi-circle =πr2 / 2
Area of a circular path or ring:
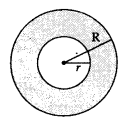
Let ‘R’ and ‘r’ he radii of two circles
Then area of shaded part = πR2 – πr2 = π(R2 – r2) = π(R + r)(R – r)
Minor arc and Major Arc: An arc length is called a major arc if the arc length enclosed by the two radii is greater than a semi-circle.
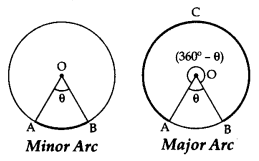
If the arc subtends angle ‘θ’ at the centre, then the
Length of minor arc =![]()
Length of major arc = ![]()
Sector of a Circle and its Area
A region of a circle is enclosed by any two radii and the arc intercepted between two radii is called the sector of a circle.
(i) A sector is called a minor sector if the minor arc of the circle is part of its boundary.
OAB is minor sector.

Area of minor sector = ![]()
Perimeter of minor sector = ![]()
Minor Segment: The region enclosed by an arc and a chord is called a segment of the circle. The region enclosed by the chord PQ & minor arc PRQ is called the minor segment.
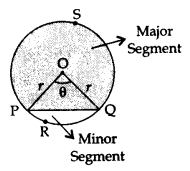
Area of Minor segment = Area of the corresponding sector – Area of the corresponding triangle
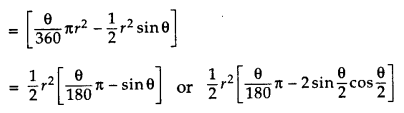
Major Segment: The region enclosed by the chord PQ & major arc PSQ is called the major segment.
Area of major segment = Area of a circle – Area of the minor segment
Area of major sector + Area of triangle