CBSE Class 10th Maths

Probability: It is the numerical measurement of the degree of certainty.

• Theoretical probability associated with an event E is defined as “If there are ‘n’ elementary events associated with a random experiment and m of these are favourable to the event E then the probability of occurrence of an event is defined by P(E) as the ratio m/n “.

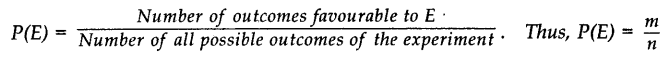
• If P(E) = 1, then it is called a ‘Certain Event’.
• If P(E) = 0, then it is called an ‘Impossible Event’.
• The probability of an event E is a number P(E) such that: 0 ≤ P(E) ≤ 1
• An event having only one outcome is called an elementary event. The sum of the probabilities of all the elementary events of an experiment is 1.
• For any event E, P(E) + P(E¯) = 1, where E¯ stands for ‘not E’. E and E¯ are called complementary events.
• Favourable outcomes are those outcomes in the sample space that are favourable to the occurrence of an event.

Sample Space
A collection of all possible outcomes of an experiment is known as sample space. It is denoted by ‘S’ and represented in curly brackets.

Examples of Sample Spaces:
A coin is tossed = Event
E₁ = Getting a head (H) on upper face
E₂ = Getting a tail (T) on upper face
S = {H, T}
Total number of outcomes = 2

Two coins are tossed = Event = E
E₁ = Getting a head on coin 1 and a tail on coin 2 = (H, T)
E₂ = Getting a head on both coin 1 and coin 2 = (H, H)
E₃ = Getting a tail on coin 1 and a head on coin 2 = (T, H)
E₄ = Getting a tail on both, coin 1 and coin 2 = (T, T)
S = {(H, T), (H, H), (T, H), (T, T)}.
Total number of outcomes = 4

• Coin: A coin has two faces termed as Head and Tail.
• Dice: A dice is a small cube which has between one to six spots or numbers on its sides, which is used in games.
• Cards: A pack of playing cards consists of four suits called Hearts, Spades, Diamonds and Clubs. Each suite consists of 13 cards.