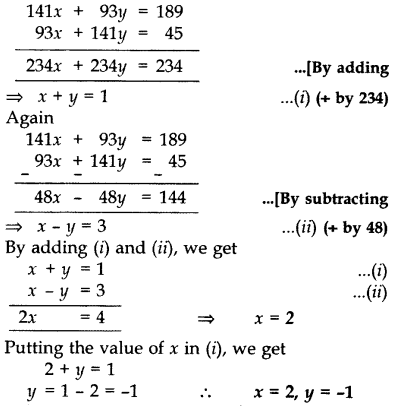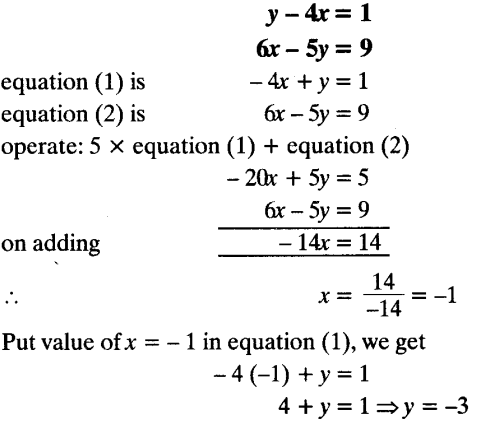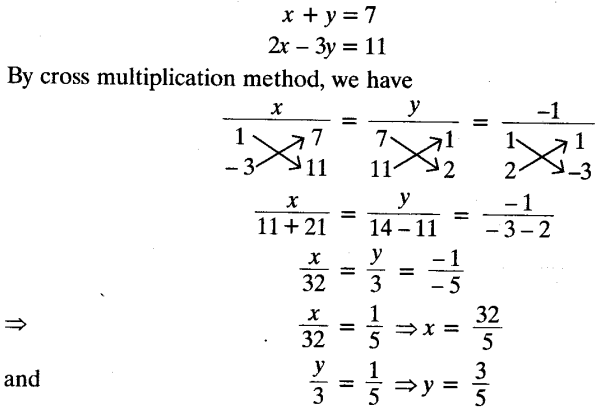An equation which can be put in the form ax+by+c=0, where a, b and c are real numbers, and a and b are not both zero, is called a linear equation in two variables x and y
Graphically or geometrically it is represented as straight line on the Cartesian plane
Each solution (x, y) of a linear equation in two variables, ax + by + c = 0, corresponds to a point on the line representing the equation
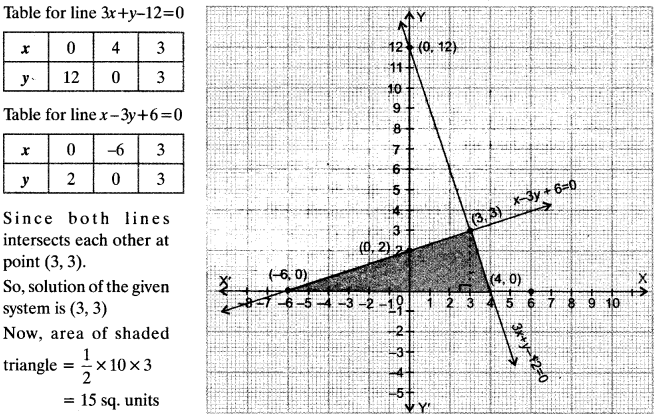
Graphical method of solution of a pair of Linear Equations

As we are showing two equations, there will be two lines on the graph.
1. If the two lines intersect each other at one particular point then that point will be the only solution of that pair of Linear Equations. It is said to be a consistent pair of equations.
2. If the two lines coincide with each other, then there will be infinite solutions as all the points on the line will be the solution for the pair of Linear Equations. It is said to be dependent or consistent pair of equations.
3. If the two lines are parallel then there will be no solution as the lines are not intersecting at any point. It is said to be an inconsistent pair of equations.
Algebraic Methods of Solving a Pair of Linear Equations
1. Substitution method
2. Elimination method
3. Cross multiplication method
Substitution method:
1. The first step to solve a pair of linear equations by the substitution method is to solve one equation for either of the variables.
2. The choice of equation or variable in a given pair does not affect the solution for the pair of equations.
3. In the next step, we’ll substitute the resultant value of one variable obtained in the other equation and solve for the other variable.
4. In the last step, we can substitute the value obtained of the variable in any one equation to find the value of the second variable.
Elimination method:
1. Multiply the equations with suitable non-zero constants, so that the coefficients of one variable in both equations become equal.
2. Subtract one equation from another, to eliminate the variable with equal coefficients.Solve for the remaining variable.
3. Substitute the obtained value of the variable in one of the equations and solve for the second variable.
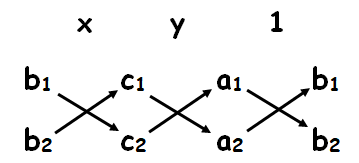
Cross - multiplication method:
Let’s consider the general form of a pair of linear equations a1x + b1y + c1 = 0 , and a2x + b2y + c2 = 0.
When a1 divided by a2 is not equal to b1 divided by b2, the pair of linear equations will have a unique solution.
To solve this pair of equations for x and y using cross-multiplication, we’ll arrange the variables x and y and their coefficients a1, a2, b1 and b2, and the constants c1 and c2 as shown below:
Some Important Solved Questions
[/dt_sc_fullwidth_section]