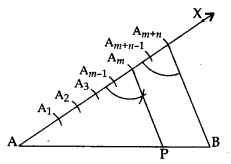
Determining a Point Dividing a given Line Segment, Internally in the given Ratio M : N
Let AB be the given line segment of length x cm. We are required to determine a point P dividing it internally in the ratio m : n.
Steps of Construction:
- Draw a line segment AB = x cm.
- Make an acute ∠BAX at the end A of AB.
- Use a compass of any radius and mark off arcs. Take (m + n) points A1, A2, … Am, Am+1, …, Am+n along AX such that AA1 = A1A2 = … = Am+n-1 , Am+n
- Join Am+nB.
- Passing through Am, draw a line AmP || Am+nB to intersect AB at P. The point P so obtained is the A required point which divides AB internally in the ratio m : n.
Construction of a Tangent at a Point on a Circle to the Circle when its Centre is Known
Steps of Construction:
- Draw a circle with centre O of the given radius.
- Take a given point P on the circle.
- Join OP.
- Construct ∠OPT = 90°.
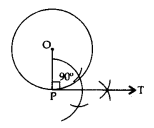
Produce TP to T’ to get TPT’ as the required tangent.
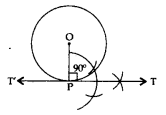
Construction of a Tangents from an External Point to a Circle when its Centre is Known
Steps of Construction:
- Draw a circle with centre O.
- Join the centre O to the given external point P.
- Draw a right bisector of OP to intersect OP at Q.
- Taking Q as the centre and OQ = PQ as radius, draw a circle to intersect the given circle at T and T’.
- Join PT and PT’ to get the required tangents as PT and PT’.

Construction of a Tangents from an External Point to a Circle when its Centre is not Known
If the centre of the circle is not known, then we first find the centre of the circle by drawing two non-parallel chords of a circle. The point of intersection of perpendicular bisectors of the chords gives the centre of the circle. Then we can proceed as above.
Construction of a Triangle Similar to a given Triangle as per given Scale Factor mn , m < n.
Let ΔABC be the given triangle. To construct a ΔA’B’C’ such that each of its sides is m/n (m < n) of the corresponding sides of ΔABC.
Steps of Construction:
- Construct a triangle ABC by using the given data.
- Make an acute angle ∠BAX, below the base AB.
- Along AX, mark n points A1, A2 …, An, such that AA1 = A1A2 = … = Am-1 Am = … An-1 An.
- Join AnB.
- From Am, draw AmB’ parallel to AnB, meeting AB at B’.
- From B’, draw B’C’ parallel to BC, meeting AC at C’.
Triangle AB’C’ is the required triangle, each of whose sides is m/n (m < n) of the corresponding sides of ΔABC.
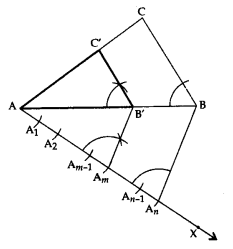
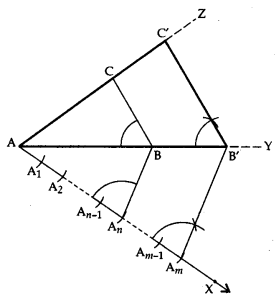
Construction of a Triangle Similar to a given Triangle as per given Scale Factor m/n , m > n.
Let ΔABC be the given triangle and we want to construct a ΔAB’C’, such that each of its sides is m/n (m > n) of the corresponding side of ΔABC.
Steps of Construction:
- Construct a ΔABC by using the given data.
- Make an acute angle ∠BAX, below the base AB. Extend AB to AY and AC to AZ.
- Along AX, mark m points A1, A2 …, An, ..Am, such that AA1 = A1A2 = A2A3 = … = An-1 An = … = Am-1 Am
- Join AnB.
- From Am, draw AmB’ parallel to AnB, meeting AY produced at B’.
- From B’, draw B’C’ parallel to BC, meeting AZ produced at C’.
- Triangle AB’C’ is the required triangle, each of whose sides is (m/n) (m > n) of the corresponding sides of ΔABC.