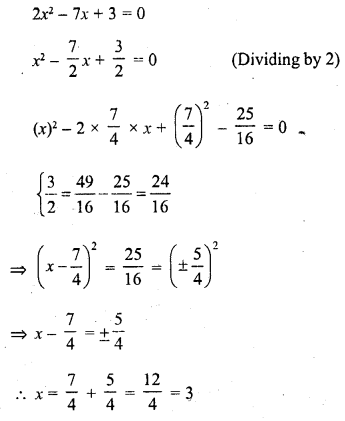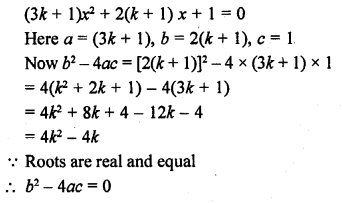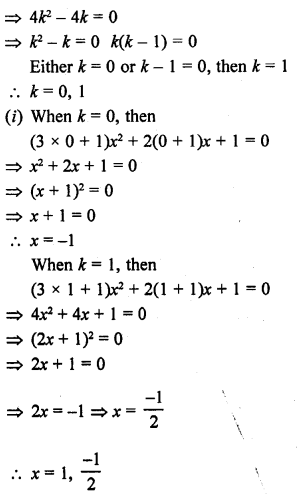The product of two consecutive positive integers is 306. Form the quadratic equation to find the integers, if x denotes the smaller integer.
Let the first number = x
Then second number = x + 1
Their product = 306
x (x + 1) = 306
⇒ x2 + x – 306 = 0
Required quadratic equation will be x2 + x – 306 = 0
The height of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, form the quadratic equation to find the base of the triangle.
Let the base of a right triangle = x
Its height = x – 7
and hypotenuse = 13 cm
⇒ By Pythagoras Theorem
(Hypotenuse)2 = (Base)2 + (Height)2
(13 )2 = x2 + (x – 7)2
⇒ 169 = x2 + x2 – 14x + 49
⇒ 2x2 – 14x + 49 – 169 = 0
⇒ 2x2 – 14x – 120 = 0
⇒ x2 – 7x – 60 = 0 (Dividing by 2)
Hence required quadratic equation will be x2 – 7x – 60 = 0
A train travels 360 km at a uniform speed. If the speed had been 5 km/hr more, it would have taken 1 hour less for the same journey. Form the quadratic equation to find the speed of the train.
Total distance = 360 km
Let the uniform speed of the train = x km/hr
Time taken = 

Find the roots of the following quadratic equation 2x² – 7x + 3 = 0 by the method of completing the square.
Find the value of k for which the quadratic equation (3k + 1) x² + 2(k + 1) x + 1 = 0 has equal roots. Also, find the roots.
![]() Here:
Here: ![]()